Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Tuya, D.; Nagaya, Yasunobu
Journal of Nuclear Engineering (Internet), 4(4), p.691 - 710, 2023/11
The Monte Carlo method is used to accurately estimate various quantities such as k-eigenvalue and integral neutron flux. However, when a distribution of a quantity is desired, the Monte Carlo method does not typically provide continuous distribution. Recently, the functional expansion tally and kernel density estimation methods have been developed to provide continuous distribution. In this paper, we propose a method to estimate a continuous distribution of a quantity using artificial neural network (ANN) model with Monte Carlo-based training data. As a proof of concept, a continuous distribution of iterated fission probability (IFP) is estimated by ANN models in two systems. The IFP distributions by the ANN models were compared with the Monte Carlo-based data and the adjoint angular neutron fluxes by the PARTISN code. The comparisons showed varying degrees of agreement or discrepancy; however, it was observed that the ANN models learned the general trend of the IFP distributions.
Tuya, D.; Nagaya, Yasunobu
Proceedings of 30th International Conference on Nuclear Engineering (ICONE30) (Internet), 8 Pages, 2023/05
Adjoint angular neutron flux is used as weighting function in various reactor applications such as calculation of kinetics parameters, importance sampling variance reduction techniques, etc. Iterated fission probability (IFP), which is proportional to a fundamental mode of adjoint angular neutron flux, has increasingly been used as weighting function in Monte Carlo calculations. The Monte Carlo based IFP methods stochastically estimate IFP for a given phase-space location. In this work, we investigated the applicability of a deep neural network for approximating an unknown underlying function, which maps from a phase-space location to an IFP in a given fissile system, from dataset produced by a Monte Carlo based IFP method. The preliminary application has been performed for the Godiva and simplified STACY cores. The comparison showed a varying degree of agreement and discrepancy between the results by the DNN and the reference results by a deterministic neutron transport code PARTISN.
Tuya, D.; Nagaya, Yasunobu
Nuclear Science and Engineering, 15 Pages, 2023/00
Times Cited Count：0 Percentile：0.01(Nuclear Science & Technology)In Monte Carlo neutron transport calculations for local response or deep penetration problems, some estimation of an importance function is generally required in order to improve their efficiency. In this work, a new recursive Monte Carlo (RMC) method, which is partly based on the original RMC method, for estimating an importance function for local variance reduction (i.e., source-detector type) problems has been developed. The new RMC method has been applied to two sample problems of varying degrees of neutron penetrations, namely a one-dimensional iron slab problem and a three-dimensional concrete-air problem. The biased Monte Carlo calculations with variance reduction parameters based on the obtained importance functions by the new RMC method have been performed to estimate detector responses in these problems. The obtained results are in agreement with those by the reference unbiased Monte Carlo calculations. Furthermore, the biased calculations offered an increase in efficiency on the order of 1 to 10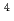
in terms of the figure of merit (FOM). The results also indicated that the efficiency increased as the neutron penetration became deeper.
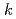-eigenvalue perturbation in Monte Carlo calculationTuya, D.; Nagaya, Yasunobu
Annals of Nuclear Energy, 169, p.108919_1 - 108919_9, 2022/05
Times Cited Count：1 Percentile：27.23(Nuclear Science & Technology)Estimating an effect of a perturbation in a fissile system on its 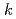-eigenvalue requires special technique called perturbation theory when the considered perturbation is small. In this study, we develop an adjoint-weighted correlated sampling (AWCS) method based on the exact perturbation theory without any approximation by combining the correlated sampling (CS) method with iterated-fission probability (IFP) based adjoint-weighting method. With the advantages of the CS method being good at providing very small uncertainty for small perturbations and the IFP-based adjoint-weighting method being suitable for continuous-energy Monte Carlo calculation, the developed AWCS method based on the exact perturbation theory offers a new rigorous approach for perturbation calculations. The obtained results by the developed AWCS method for verification problems involving Godiva and simplified STACY density perturbations showed good agreement with the reference calculations.
Takezawa, Hiroki*; Tuya, D.; Obara, Toru*
Nuclear Science and Engineering, 195(11), p.1236 - 1246, 2021/11
Times Cited Count：0 Percentile：0.01(Nuclear Science & Technology)This study introduces new methodologies for integrating fission reactions induced by delayed neutrons into the Multi-Region Integral Kinetic (MIK) code by using a Monte Carlo neutron transport calculation. First, it was confirmed that it is feasible to solve the Integral Kinetic Model (IKM) with delayed neutrons by the forward Euler discretization method in terms of the number of time steps. This can be done with the help of the law of radioactive decay to reflect the delay in the emission of delayed neutrons in the discretized IKM. Second, a new Monte Carlo-based methodology was introduced for calculating the cumulative distribution functions of secondary fission induced by prompt and delayed neutrons. These functions are necessary for the discretized IKM. The results of preliminary verification using the Godiva reactor confirmed the applicability of the new Monte Carlo-based methodology.
Tuya, D.; Nagaya, Yasunobu
no journal, ,
Tuya, D.; Nagaya, Yasunobu
no journal, ,
Tuya, D.
no journal, ,
A new continuous-energy neutron transport Monte Carlo solver Solomon is under development at JAEA. The Solomon solver has a distinct capability of calculating criticality of continuously-varying random media expressed with randomized Weierstrass function. One important feature of any Monte Carlo transport code is a capability for sensitivity/uncertainty analysis. This presentation discusses the development of k-eigenvalue sensitivity coefficient capability for the Solomon solver.
