Solutions of partial differential equations with the CIP-BS method

CIP-BS法を用いた偏微分方程式の解法

内海 隆行*; 木村 英雄

Utsumi, Takayuki*; Kimura, Hideo

CIP-BS法を用いて3種類(方物型,楕円型,双曲型)の偏微分方程式を解き、解の精度と安定性について考察した。2次までの微係数を考慮するCIP-BS2法は1次までの微係数を考慮するCIP-BS1法よりも高い精度で解を得ることができ、放物型と双曲型の方程式に対してCIP-BS法は原理的に保存性を有することを示した。CIP-BS法は空間微分が不連続になる特異点を計算体系に有する問題を解くことが可能であることを示し、偏微分方程式の普遍的な解法であることを示した。

In this paper, we show that a new numerical method, the Constrained Interpolation Profile - Basis Set (CIP-BS) method, can solve partial differential equations (PDEs) with high accuracy and can be a universal solver by presenting examples for the solutions of typical parabolic, hyperbolic, and elliptic equations. Here, we present the numerical errors caused by this method, and illustrate that the solutions by the CIP-BS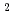 method, in which fifth order polynomials are used to constrain the values and first and second order spatial derivatives, are highly refined compared to those by the CIP-BS 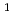method, in which third order polynomials are used to constrain the values and first order spatial derivatives. The fact that this method can unambiguously solve PDEs with an one-to-one correspondence to analytical requirements is also shown for PDEs including singular functions like the Dirac delta function with Dirichet or Neumann boundary conditions. This method is straightforwardly applicable to PDEs describing complex physical and engineering problems.