Monte Carlo uncertainty quantification of the effective delayed neutron fraction

Iwamoto, Hiroki   ; Stankovskiy, A.*; Fiorito, L.*; Van den Eynde, G.*

The applicability of Monte Carlo techniques, namely the Monte Carlo sensitivity method and the random-sampling method, for uncertainty quantification of the effective delayed neutron fraction 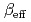is investigated using the continuous-energy Monte Carlo transport code, MCNP, from the perspective of statistical convergence issues. This study focuses on the nuclear data as one of the major sources of 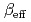uncertainty. For validation of the calculated 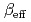, a critical configuration of the VENUS-F zero-power reactor was used. It is demonstrated that Chiba's modified 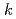-ratio method is superior to Bretscher's prompt 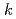-ratio method in terms of reducing the statistical uncertainty in calculating not only 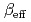but also its sensitivities and the uncertainty due to nuclear data. From this result and a comparison of uncertainties obtained by the Monte Carlo sensitivity method and the random-sampling method, it is shown that the Monte Carlo sensitivity method using Chiba's modified 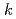-ratio method is the most practical for uncertainty quantification of 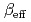. Finally, total 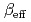uncertainty due to nuclear data for the VENUS-F critical configuration is determined to be approximately 2.7% with JENDL-4.0u, which is dominated by the delayed neutron yield of 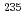U.