Establishment of numerical model to investigate heat transfer and flow characteristics by using scale model of vessel cooling system for HTTR

HTTRの炉容器冷却設備スケールモデルを用いた伝熱流動数値解析モデルの構築

高田 昌二; Ngarayana, I. W.*; 中津留 幸裕*; 寺田 敦彦  ; 村上 健太*; 澤 和彦*

Takada, Shoji; Ngarayana, I. W.*; Nakatsuru, Yukihiro*; Terada, Atsuhiko; Murakami, Kenta*; Sawa, Kazuhiko*

高温工学試験研究炉(HTTR)を使った炉心冷却喪失試験では、財産保護上の観点から、炉容器冷却設備(VCS)において自然対流により加熱される構造物の温度分布の評価精度向上を課題としている。伝熱流動数値解析コードFLUENTをHTTRのVCSに適用するために、予測精度を維持しつつ計算資源を節約できる合理的な2次元モデルの構築を始めた。本評価モデルの検証のため、HTTR用VCSの1/6スケールモデルによる構造物の温度に関する試験結果を使用し、解析による計算結果と比較した。本試験データは、圧力容器の温度を200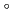C前後に設定することで、全除熱量における自然対流伝熱の割合を20%前後と有意なレベルの伝熱現象として測定したものである。自然対流による上昇流の影響で高温となる圧力容器上部の伝熱流動特性の評価精度向上のためには、実形状の模擬および自然対流に適した乱流モデルの選定が重要となる。乱流モデルとして、剥離,再付着及び遷移流れを考慮できるk-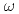-SSTモデルを選定し、従来のk-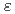モデルでは再現されなかった圧力容器の温度分布の試験結果とよく一致していることを確認した。このことから、k-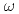-SSTモデルは、圧力容器上部の温度分布を剥離、再付着および遷移流れを再現できたと考えられ、本モデルはVCSの温度評価の精度向上に有効であることを明らかにした。

In the loss of core cooling test using HTTR, a technical issue is to improve prediction accuracy of temperature distribution of components in vessel cooling system (VCS). An establishment of reasonable 2D model was started by using numerical code FLUENT, which was validated using the test data by 1/6 scale model of VCS for HTTR. The pressure vessel (PV) temperature was set around 200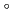C attributed to relatively high ratio of natural convection heat transfer around 20% in total heat removal, which is useful for code to experiment benchmark to improve prediction accuracy. It is necessary to confirm heat transfer flow characteristics around the top of PV which is heated up by natural convection flow which was considered to be affected by separation, re-adhesion and transition flow. The k-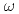-SST model was selected for turbulent calculation attributed to predict the effects mentioned above adequately. The numerical results using the k-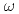-SST model reproduced the temperature distribution of PV especially the top region which is considered to be affected by separation, re-adhesion and transition flow in contract to that using k- 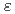model which does not account the effects.