Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Yamada, Susumu; Okumura, Masahiko; Imamura, Toshiyuki*; Machida, Masahiko
Japan Journal of Industrial and Applied Mathematics, 28(1), p.141 - 151, 2011/04
Times Cited Count:2 Percentile:21.15(Mathematics, Applied)The density-matrix renormalization group (DMRG) method is widely used by computational physicists as a high accuracy tool to explore the ground state in large quantum lattice models, e.g., Heisenberg and Hubbard models, which are well-known standard models describing interacting spins and electrons, respectively, in solid states. After the DMRG method was originally developed for 1-D lattice/chain models, some specific extensions toward 2-D lattice (n-leg ladder) models have been proposed. However, high accuracy as obtained in 1-D models is not always guaranteed in their extended versions because the original exquisite algorithm is partly lost. Thus, we choose an alternative way. It is a direct 2-D extension of DMRG method which instead demands an enormously large memory space, but the memory explosion is resolved by parallelizing the DMRG code with performance tuning. The parallelized direct extended DMRG shows a good accuracy like 1-D models and an excellent parallel efficiency as the number of states kept increases. This success promises accurate analysis on large 2-D (n-leg ladder) quantum lattice models in the near future when peta-flops parallel supercomputers are available.
Ota, Yukihiro; Machida, Masahiko; Koyama, Tomio*
Physica C, 470(Suppl.1), p.S489 - S490, 2010/12
Times Cited Count:0 Percentile:0(Physics, Applied)We microscopically study inter-grain Josephson current in iron-pnictide superconductors. The theoretical examination predicts that the inter-grain Josephson current is significantly reduced by 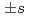 -wave symmetry as the incoherent tunneling process becomes dominant and the density of states and the gap amplitude between two bands are identical. In addition, we suggest important points to improve the inter-grain critical current density.
-wave symmetry as the incoherent tunneling process becomes dominant and the density of states and the gap amplitude between two bands are identical. In addition, we suggest important points to improve the inter-grain critical current density.
Yamada, Susumu; Okumura, Masahiko; Machida, Masahiko
Journal of the Physical Society of Japan, 78(9), p.094004_1 - 094004_5, 2009/09
Times Cited Count:11 Percentile:56.86(Physics, Multidisciplinary)We parallelize the density-matrix renormalization group method to directly extend it to 2-dimensional (n-leg) quantum lattice models. The parallelization is made mainly on the diagonalization for the superblock Hamiltonian since the part requires enormous memory space as the leg number n increases. The superblock Hamiltonian is divided into three parts, and the correspondent superblock vectors are transformed into matrices, whose elements are uniformly distributed into processors. The parallel efficiency shows a high rate as the number of the states kept m increases, and the obtained ground-state energy rapidly converges within a few sweeps. Furthermore, the present algorithm reaches the ground-state which satisfies the Lieb-Mattis theorem with much less m than a different indirect algorithm.
Yamada, Susumu; Imamura, Toshiyuki*; Machida, Masahiko
Nihon Keisan Kogakkai Rombunshu (Internet), 2009(15), 12 Pages, 2009/09
We parallelize the density matrix renormalization group (DMRG) method, which is a groundstate solver for one-dimensional quantum lattice systems. The parallelization allows us to extend the applicable range of the DMRG to multiple leg ladders or quasi two-dimension cases. Such an extension is regarded to bring about several breakthroughs in quantum physics, chemistry, nano-device engineering, and so on. The parallelization requires an all-to-all communication which involves all processes. Such a communication is not suitable for multi-core clusters, which are presently the main stream of the parallel computer, because the network bandwidth should be shared by a large number of processes. Therefore, we propose a new communication strategy to eliminate the all-to-all communication by rearranging a data distribution. We evaluate performance of the new strategy on "SGI Altix 3700Bx2" (single-core system) and "T2K Open Supercomputer (Todai Combined Cluster)" (quad-core system) and confirm that the strategy is quite crucial for typical multi-core systems like T2K.
Ota, Yukihiro; Machida, Masahiko; Koyama, Tomio*; Matsumoto, Hideki*
Physical Review Letters, 102(23), p.237003_1 - 237003_4, 2009/06
Times Cited Count:62 Percentile:89.03(Physics, Multidisciplinary)Using the functional integral method, we construct a theory of heterotic superconductor-insulator-superconductor Josephson junctions between one- and two-gap superconductors. The theory predicts the presence of in-phase and out-of-phase collective oscillation modes of superconducting phases. The former corresponds to the Josephson plasma mode whose frequency is drastically reduced for 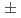
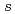 -wave symmetry, and the latter is a counterpart of Leggett's mode in Josephson junctions. We also reveal that the critical current and the Fraunhofer pattern strongly depend on the symmetry type of the two-gap superconductor.
-wave symmetry, and the latter is a counterpart of Leggett's mode in Josephson junctions. We also reveal that the critical current and the Fraunhofer pattern strongly depend on the symmetry type of the two-gap superconductor.
Okumura, Masahiko; Yamada, Susumu; Taniguchi, Nobuhiko*; Machida, Masahiko
Physical Review B, 79(18), p.184417_1 - 184417_5, 2009/05
Times Cited Count:2 Percentile:11.68(Materials Science, Multidisciplinary)In order to study an interplay of disorder, correlation, and spin imbalance on antiferromagnetism, we systematically explore the ground state of one-dimensional spin-imbalanced Anderson-Hubbard model by using the density-matrix renormalization-group method. We find that disorders localize the antiferromagnetic spin-density wave induced by imbalanced fermions and the increase in the disorder magnitude shrinks the areas of the localized antiferromagnetized regions. Moreover, the antiferromagnetism finally disappears above a large disorder. The localization behaviors are observable in atomic Fermi gases loaded on optical lattices as broadening of the momentum distribution of the spin density by using the Stern-Gerlach type of time-of-fight imaging.
Okumura, Masahiko; Yamada, Susumu; Machida, Masahiko
Soryushiron Kenkyu, 116(6), p.F69 - F71, 2009/02
no abstracts in English
Imamura, Toshiyuki*; Yamada, Susumu; Machida, Masahiko
Joho Shori Gakkai Kenkyu Hokoku 2007-HPC-111, p.167 - 172, 2007/08
no abstracts in English
Owada, Kenji; Namikawa, Kazumichi; Mizuki, Junichiro; Shimomura, Susumu*; Nakao, Hironori*; Ito, Kazuki*; Matsushita, Mitsuyoshi*; Yoneda, Yasuhiro; Murakami, Yoichi*; Hirota, Kazuma*
Transactions of the Materials Research Society of Japan, 32(1), p.7 - 10, 2007/03
An X-ray speckle pattern well reflects a particle or domain alignment on the inside of materials. Detecting the alignment is important for understanding a function of the materials such as ferroelectric, piezoelectric materials, photonic crystals and so on. We have thus constructed the apparatus for coherent X-ray diffraction at BL22XU@SPring-8, high quality slits for obtaining the full coherent X-ray beam, high resolution X-ray CCD camera for obtaining the well-resolved speckle pattern, and so on. By using the devices, we have successfully observed the speckle pattern from Cu Au, the ferroelectric material PZN-9%PT (91%Pb(Zn
Au, the ferroelectric material PZN-9%PT (91%Pb(Zn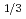 Nb
Nb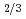 )O
)O -9%PbTiO
-9%PbTiO ) and Sr-doped BaTiO
) and Sr-doped BaTiO . The 2DFFT image gives us a spatial autocorrelation function which includes the information of the arrangement of the domains in the crystal within micrometers scale.
. The 2DFFT image gives us a spatial autocorrelation function which includes the information of the arrangement of the domains in the crystal within micrometers scale.
Okumura, Masahiko; Onishi, Hiroaki; Yamada, Susumu; Machida, Masahiko
no journal, ,
no abstracts in English
Okumura, Masahiko; Yamada, Susumu; Machida, Masahiko
no journal, ,
no abstracts in English
Okumura, Masahiko; Onishi, Hiroaki; Yamada, Susumu; Machida, Masahiko
no journal, ,
no abstracts in English
Okumura, Masahiko; Onishi, Hiroaki; Yamada, Susumu; Machida, Masahiko
no journal, ,
no abstracts in English
Okumura, Masahiko; Yamada, Susumu; Machida, Masahiko; Aoki, Hideo*
no journal, ,
no abstracts in English
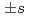 -wave in iron-based superconductors
-wave in iron-based superconductorsOta, Yukihiro; Nakai, Noriyuki; Nakamura, Hiroki; Machida, Masahiko; Inotani, Daisuke*; Ohashi, Yoji*; Koyama, Tomio*; Matsumoto, Hideki*
no journal, ,
An enormous amount of studies has been devoted to the identification of the pairing symmetry in iron-based superconductors. We show a theory of Josephson junctions with multi-gap superconductors. We focus on a heterotic (multi-band)superconductor- insulator-(one-band)superconductor junction. We derive the Ambegaokar-Baratoff relation. We evaluate a lower bound of 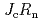 for
for 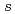 -wave without sign change, which may correspond to a upper bound for
-wave without sign change, which may correspond to a upper bound for 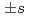 -wave. Next, we discuss how a fluctuation of relative phases between the gaps and the symmetry modify the Shapiro step. Thus, we propose a direct method to identify
-wave. Next, we discuss how a fluctuation of relative phases between the gaps and the symmetry modify the Shapiro step. Thus, we propose a direct method to identify 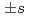 -wave.
-wave.
Ota, Yukihiro; Machida, Masahiko; Koyama, Tomio*; Aoki, Hideo*
no journal, ,
One important way to characterize multi-band superconductors should be to look at their collective modes, which are expected to reflect the broken gauge symmetry that involves multi-bands. We extend Leggett's analysis for a massive out-of-phase mode coexisting with the Nambu-Goldstone mode in two-band superconductors to the case where there are three or more bands. Crucial is to classify the inter-band Josephson coupling energy which is the origin of the Leggett's modes. Three-band superconductors are shown to accommodate more than one collective modes, which are classified in terms of the "dynamical class" that distinguishes the action of the inter-band Josephson coupling. The mass of the multiple Leggett's modes is then shown to dramatically depend on the class. We expect that the present prediction can be tested in the iron-based superconductor (with a gap function involving three bands).
Ota, Yukihiro; Machida, Masahiko; Koyama, Tomio*; Aoki, Hideo*
no journal, ,
One important way to characterize multi-band superconductors should be to look at their collective excitation modes, which are expected to reflect the broken gauge symmetry that involves multi-bands. Here we extend Leggett's analysis for a massive out-of-phase collective mode coexisting with the Nambu-Goldstone mode in two-band superconductors to the case where there are three or more bands. Crucial is to classify the inter-band Josephson coupling energy which is the origin of the Leggett's collective modes. Three-band superconductors are shown to accommodate more than one collective modes, which are classified in terms of the "dynamicalclass" that distinguishes the parity of the inter-band Josephson current. The mass of the multiple Leggett's modes is then shown to dramatically depend on the class. We expect that the present prediction can be tested in the iron-based superconductor (with a gap function involving three bands).
Yamada, Susumu; Imamura, Toshiyuki*; Okumura, Masahiko; Igarashi, Ryo; Machida, Masahiko
no journal, ,
no abstracts in English
Yamada, Susumu; Okumura, Masahiko; Igarashi, Ryo; Machida, Masahiko
no journal, ,
no abstracts in English
Ota, Yukihiro; Machida, Masahiko; Koyama, Tomio*
no journal, ,
Recent discovery of iron-based superconductors has triggered the study of multi-gap superfluidity/superconductivity. We derive the Ginzburg-Landau (GL) equation in a  -gap system, which is a simultaneous non-linear partial differential equation. The system has not only a usual non-linear term but also coupling between different gaps (i.e., inter-band Josephson coupling). We show that this equation has non-trivial class of the solutions based on the linearized GL equation when
-gap system, which is a simultaneous non-linear partial differential equation. The system has not only a usual non-linear term but also coupling between different gaps (i.e., inter-band Josephson coupling). We show that this equation has non-trivial class of the solutions based on the linearized GL equation when 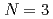 . We stress that such a class never exist in the case of
. We stress that such a class never exist in the case of 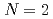 . We will also discuss generalization of the present result.
. We will also discuss generalization of the present result.