Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Onodera, Naoyuki; Idomura, Yasuhiro; Hasegawa, Yuta; Shimokawabe, Takashi*; Aoki, Takayuki*
Keisan Kogaku Koenkai Rombunshu (CD-ROM), 26, 3 Pages, 2021/05
We develop a mixed-precision preconditioner for the pressure Poisson equation in a two-phase flow CFD code JUPITER-AMR. The multi-grid (MG) preconditioner is constructed based on the geometric MG method with a three- stage V-cycle, and a cache-reuse SOR (CR-SOR) method at each stage. The numerical experiments are conducted for two-phase flows in a fuel bundle of a nuclear reactor. The MG-CG solver in single-precision shows the same convergence histories as double-precision, which is about 75% of the computational time in double-precision. In the strong scaling test, the MG-CG solver in single-precision is accelerated by 1.88 times between 32 and 96 GPUs.
Onodera, Naoyuki; Idomura, Yasuhiro; Hasegawa, Yuta; Yamashita, Susumu; Shimokawabe, Takashi*; Aoki, Takayuki*
Proceedings of International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia 2021) (Internet), p.120 - 128, 2021/01
Times Cited Count：0 Percentile：0.00(Computer Science, Hardware & Architecture)We develop a multigrid preconditioned conjugate gradient (MG-CG) solver for the pressure Poisson equation in a two-phase flow CFD code JUPITER. The MG preconditioner is constructed based on the geometric MG method with a three-stage V-cycle, and a RB-SOR smoother and its variant with cache-reuse optimization (CR-SOR) are applied at each stage. The numerical experiments are conducted for two-phase flows in a fuel bundle of a nuclear reactor. The MG-CG solvers with the RB-SOR and CR-SOR smoothers reduce the number of iterations to less than 15% and 9% of the original preconditioned CG method, leading to 3.1- and 5.9-times speedups, respectively. The obtained performance indicates that the MG-CG solver designed for the block-structured grid is highly efficient and enables large-scale simulations of two-phase flows on GPU based supercomputers.
Onodera, Naoyuki; Idomura, Yasuhiro; Asahi, Yuichi; Hasegawa, Yuta; Shimokawabe, Takashi*; Aoki, Takayuki*
Dai-34-Kai Suchi Ryutai Rikigaku Shimpojiumu Koen Rombunshu (Internet), 2 Pages, 2020/12
We develop a multigrid preconditioned conjugate gradient (MG-CG) solver for the pressure Poisson equation in a two-phase flow CFD code JUPITER. The code is written in C++ and CUDA to keep the portability on multi-platforms. The main kernels of the CG solver achieve reasonable performance as 0.4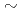 
0.75 of the roofline performances, and the performances of the MG-preconditioner are also reasonable on NVIDIA GPU and Intel CPU. However, the performance degradation of the SpMV kernel on ARM is significant. It is confirmed that the optimization does not work if any functions are included in the loop.
Idomura, Yasuhiro; Onodera, Naoyuki; Yamada, Susumu; Yamashita, Susumu; Ina, Takuya*; Imamura, Toshiyuki*
Supa Kompyuteingu Nyusu, 22(5), p.18 - 29, 2020/09
A communication avoiding multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against the conventional Krylov methods. The CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with 90 billion DOFs, and its performance is compared against the preconditioned CG solver. In this benchmark, the number of iterations is reduced to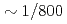 
, and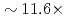 
speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
Onodera, Naoyuki; Idomura, Yasuhiro; Ali, Y.*; Shimokawabe, Takashi*; Aoki, Takayuki*
Keisan Kogaku Koenkai Rombunshu (CD-ROM), 25, 4 Pages, 2020/06
We have developed the stencil-based CFD code JUPITER for simulating three-dimensional multiphase flows. A GPU-accelerated Poisson solver based on the preconditioned conjugate gradient (P-CG) method with a multigrid preconditioner was developed for the JUPITER with block-structured AMR mesh. All Poisson kernels were implemented using CUDA, and the GPU kernel function is well tuned to achieve high performance on GPU supercomputers. The developed multigrid solver shows good convergence of about 1/7 compared with the original P-CG method, and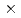 
3 speed up is achieved with strong scaling test from 8 to 216 GPUs on TSUBAME 3.0.
Ohashi, Kunihide*; Hino, Takanori*; Kobayashi, Hiroshi*; Onodera, Naoyuki; Sakamoto, Nobuaki*
Journal of Marine Science and Technology, 24(3), p.884 - 901, 2019/09
Times Cited Count：23 Percentile：78.52(Engineering, Marine)An unsteady Reynolds averaged Navier-Stokes solver with a structured overset grid method has been developed. Velocity pressure coupling is achieved using an artificial compressibility approach, spatial discretization is based on a FVM. Body motions are considered using the grid deformation technique and grid velocities in the convective term. The full multigrid (FMG) method is applied to obtain fast convergence. The cell flag on a coarse grid level is determined using the cell flag on a fine grid level. In the coarse and fine grid level calculations at the FMG stage, the data are interpolated until the finest grid level is achieved at an overset update interval. Then, the data are updated based on the overset relations at the finest grid level and then transferred to a coarser grid level. The computations for flows around a hull form, including an unsteady simulation with regular waves, are demonstrated.
Onodera, Naoyuki; Idomura, Yasuhiro; Asahi, Yuichi; Hasegawa, Yuta; Shimokawabe, Takashi*; Aoki, Takayuki*
no journal, ,
This paper presents performance studies of a multigrid (MG) Poisson solver on a block-structured adaptive mesh refinement (block-AMR) method on CPU and GPU supercomputers. The block-AMR method is efficient solutions of the nuclear reactor which is composed of complicated structures. We implement a three-stage V-cycle MG method and the calculation is accelerated by using a mixed precision techniques. For a large-scale Poisson problem with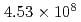 
cells, the developed MG-CG method reduced the number of iterations to less than 30% and achieved 2 times speedup compared with the original preconditioned CG method on the GPU-supercomputer TSUBAME. This kind of performance studies are useful for designing advanced preconditioners in terms of robustness, computational precision, thread parallelization, and cache size on each architecture.
Imamura, Toshiyuki*; Idomura, Yasuhiro; Ina, Takuya*; Yamashita, Susumu; Onodera, Naoyuki; Ali, Y.*; Yamada, Susumu
no journal, ,
Towards exascale computing on the Post-K computer, a novel matrix solvers are developed by using communication avoiding algorithms. In this talk, we review two main approaches used in the three-dimensional thermal hydraulic multi-phase CFD code, JUPITER. One is a communication avoiding Krylov sub-space method, in which multiple basis vectors are generated and orthogonalized at once to reduce global collective communications. The other is a Krylov sub-space method with multi-grid preconditioning, which dramatically improve convergence property and reduce the number of iterations, and thus, global collective communications. We compare these approaches on the latest many core platform.
Onodera, Naoyuki; Idomura, Yasuhiro; Yamashita, Susumu; Hasegawa, Yuta; Shimokawabe, Takashi*; Aoki, Takayuki*
no journal, ,
We develop a multigrid preconditioned conjugate gradient (MG-CG) solver for the pressure Poisson equation in a two-phase flow CFD code JUPITER. The numerical experiments are conducted for two-phase flows in a fuel bundle of a nuclear reactor. Thanks to the block-structured AMR data format, grids inside fuel pins are removed without performance degradation, and the total number of grids is reduced to 70% of the original Cartesian grid. The MG-CG solvers reduce the number of iterations to less than 15% of the original preconditioned CG method, leading to 3.1-times speedups.
