Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
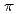-flux modelGhadimi, R.*; Hori, Masahiro*; 杉本 貴則*; 遠山 貴己
Physical Review B, 108(12), p.125104_1 - 125104_18, 2023/09
被引用回数：6 パーセンタイル：56.18(Materials Science, Multidisciplinary)Motivated by topological equivalence between an extended Haldane model and a chiral-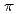-flux model on a square lattice, we apply 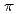-flux models to two-dimensional bipartite quasicrystals with rhombus tiles in order to investigate topological properties in aperiodic systems. Topologically trivial 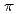-flux models in the Ammann-Beenker tiling lead to massively degenerate confined states whose energies and fractions differ from the zero-flux model. This is different from the 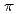-flux models in the Penrose tiling, where confined states only appear at the center of the bands as is the case of a zero-flux model. Additionally, Dirac cones appear in a certain 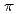-flux model of the Ammann-Beenker approximant, which remains even if the size of the approximant increases. Nontrivial topological states with nonzero Bott index are found when staggered tile-dependent hoppings are introduced in the 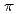-flux models. This finding suggests a direction in realizing nontrivial topological states without a uniform magnetic field in aperiodic systems.
Ghadimi, R.*; 杉本 貴則*; 遠山 貴己
Physical Review B, 106(20), p.L201113_1 - L201113_6, 2022/11
被引用回数：5 パーセンタイル：40.97(Materials Science, Multidisciplinary)It is now possible to use quasicrystals to search for novel topological phenomena enhanced by their peculiar structure characterized by an irrational number and high-dimensional primitive vectors. Here, we extend the concept of a topological insulator with an emerging staggered local magnetic flux (i.e., without external fields), similar to Haldane's honeycomb model, to the Penrose lattice as a quasicrystal. The Penrose lattice consists of two different tiles, where the ratio of the numbers of tiles corresponds to an irrational number. Contrary to periodic lattices, the periodicity of the energy spectrum with respect to the magnetic flux no longer exists, reflecting the irrational number in the Penrose lattice. Calculating the Bott index as a topological invariant, we find topological phases appearing in a fractal energy spectrum similar to the Hofstadter butterfly. More intriguingly, by folding the one-dimensional aperiodic magnetic flux into a two-dimensional periodic flux space, the fractal structure of the energy spectrum is extended to a higher dimension, whose section corresponds to the Hofstadter butterfly.
Ghadimi, R.*; 杉本 貴則*; 田中 佳織*; 遠山 貴己
Physical Review B, 104(14), p.144511_1 - 144511_10, 2021/10
被引用回数：31 パーセンタイル：86.56(Materials Science, Multidisciplinary)We propose realization of non-Abelian topological superconductivity in two-dimensional quasicrystals by the same mechanism as in crystalline counterparts. Specifically, we study a two-dimensional electron gas in Penrose and Ammann-Beenker quasicrystals with Rashba spin-orbit coupling, perpendicular Zeeman magnetic field, and conventional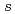 
-wave superconductivity. We find that topological superconductivity with broken time-reversal symmetry is realized in both Penrose and Ammann-Beenker quasicrystals at low filling, where the Bott index is unity. The topological nature of this phase is confirmed by the existence of a zero-energy surface bound state and the chiral propagation of a wave packet projected onto the midgap bound state along the surfaces. Furthermore, we confirm the existence of a single Majorana zero mode each in a vortex at the center of the system and along the surfaces, signifying the non-Abelian character of the system when the Bott index is unity.
Ghadimi, R.*; 杉本 貴則*; 遠山 貴己
Physical Review B, 102(22), p.224201_1 - 224201_9, 2020/12
被引用回数：14 パーセンタイル：58.53(Materials Science, Multidisciplinary)We examine the Bose-Hubbard model in the Penrose lattice based on inhomogeneous mean-field theory. Since the averaged coordination number in the Penrose lattice is four, the mean-field phase diagram consisting of the Mott insulator (MI) and superfluid (SF) phase is similar to that of the square lattice. However, the spatial distribution of the Bose condensate in the SF phase is significantly different from uniform distribution in the square lattice. We find a fractal structure in its distribution near the MI-SF phase boundary. The emergence of the fractal structure is a consequence of the cooperative effect between quasiperiodicity in the Penrose lattice and criticality at the phase transition.
