Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Hasegawa, Yuta; Onodera, Naoyuki; Asahi, Yuichi; Ina, Takuya; Imamura, Toshiyuki*; Idomura, Yasuhiro
Fluid Dynamics Research, 55(6), p.065501_1 - 065501_25, 2023/11
Times Cited Count：1 Percentile：14.16(Mechanics)We investigate the applicability of the data assimilation (DA) to large eddy simulations (LESs) based on the lattice Boltzmann method (LBM). We carry out the observing system simulation experiment of a two-dimensional (2D) forced isotropic turbulence, and examine the DA accuracy of the nudging and the local ensemble transform Kalman filter (LETKF) with spatially sparse and noisy observation data of flow fields. The advantage of the LETKF is that it does not require computing spatial interpolation and/or an inverse problem between the macroscopic variables (the density and the pressure) and the velocity distribution function of the LBM, while the nudging introduces additional models for them. The numerical experiments with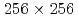 
grids and 10% observation noise in the velocity showed that the root mean square error of the velocity in the LETKF with 
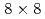observation points (
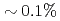of the total grids) and 64 ensemble members becomes smaller than the observation noise, while the nudging requires an order of magnitude larger number of observation points to achieve the same accuracy. Another advantage of the LETKF is that it well keeps the amplitude of the energy spectrum, while only the phase error becomes larger with more sparse observation. From these results, it was shown that the LETKF enables robust and accurate DA for the 2D LBM with sparse and noisy observation data.
Ina, Takuya; Idomura, Yasuhiro; Imamura, Toshiyuki*; Onodera, Naoyuki
Proceedings of International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia 2023) (Internet), p.29 - 34, 2023/02
Mixed precision Krylov solvers with the Jacobi preconditioner often show significant convergence degradation when the Jacobi preconditioner is computed in low precision such as FP16 and BF16. It is found that this convergence degradation is attributed to loss of diagonal dominance due to roundoff errors in data conversion. To resolve this issue, we propose a new data conversion method, which is designed to keep diagonal dominance of the original matrix data. The proposed method is tested by computing the Poisson equation using the conjugate gradient method, the general minimum residual method, and the biconjugate gradient stabilized method with the FP16/BF16 Jacobi preconditioner on NVIDIA V100 GPUs. Here, the new data conversion is implemented by switching the round-nearest, round-up, round-down, and round-towards-zero intrinsics in CUDA, and is called once before the main iteration. Therefore, the cost of the new data conversion is negligible. When the coefficients of matrix is continuously changed by scaling the linear system, the conventional data conversion based on the round-nearest intrinsic shows periodic changes of the convergence property depending on the difference of the roundoff errors between diagonal and off-diagonal coefficients. Here, the period and magnitude of the convergence degradation depend on the bit length of significand. On the other hand, the proposed data conversion method is shown to fully avoid the convergence degradation, and robust mixed precision computing is enabled for the Jacobi preconditioner without extra overheads.
Hasegawa, Yuta; Imamura, Toshiyuki*; Ina, Takuya; Onodera, Naoyuki; Asahi, Yuichi; Idomura, Yasuhiro
Proceedings of 13th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Heterogeneous Systems (ScalAH22) (Internet), p.10 - 17, 2022/00
The ensemble data assimilation of computational fluid dynamics simulations based on the lattice Boltzmann method (LBM) and the local ensemble transform Kalman filter (LETKF) is implemented and optimized on a GPU supercomputer based on NVIDIA A100 GPUs. To connect the LBM and LETKF parts, data transpose communication is optimized by overlapping computation, file I/O, and communication based on data dependency in each LETKF kernel. In two dimensional forced isotropic turbulence simulations with the ensemble size of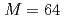 
and the number of grid points of 
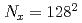, the optimized implementation achieved 
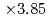speedup from the naive implementation, in which the LETKF part is not parallelized. The main computing kernel of the local problem is the eigenvalue decomposition (EVD) of 
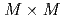real symmetric dense matrices, which is computed by a newly developed batched EVD in EigenG. The batched EVD in EigenG outperforms that in cuSolver, and 
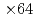speedup was achieved.
Yamada, Susumu; Imamura, Toshiyuki*; Machida, Masahiko
Supercomputing Frontiers, p.1 - 19, 2022/00
Times Cited Count：1 Percentile：37.95(Computer Science, Theory & Methods)no abstracts in English
Ina, Takuya*; Idomura, Yasuhiro; Imamura, Toshiyuki*; Yamashita, Susumu; Onodera, Naoyuki
Proceedings of 12th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems ScalA21) (Internet), 8 Pages, 2021/11
Times Cited Count：3 Percentile：65.51(Computer Science, Software Engineering)A new mixed-precision preconditioner based on the iterative refinement (IR) method is developed for preconditioned conjugate gradient (P-CG) and multigrid preconditioned conjugate gradient (MGCG) solvers in a multi-phase thermal-hydraulic CFD code JUPITER. In the IR preconditioner, all data is stored in FP16 to reduce memory access, while all computation is performed in FP32. The hybrid FP16/32 implementation keeps the similar convergence property as FP32, while the computational performance is close to FP16. The developed solvers are optimized on Fugaku (A64FX), and applied to ill-conditioned matrices in JUPITER. The P-CG and MGCG solvers with the new IR preconditioner show excellent strong scaling up to 8,000 nodes, and at 8,000 nodes, they are respectively accelerated up to 4.86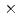
and 2.39 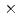from the conventional ones on Oakforest-PACS (KNL).
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Dai-34-Kai Suchi Ryutai Rikigaku Shimpojiumu Koen Rombunshu (Internet), 6 Pages, 2020/12
A new communication avoiding (CA) Krylov solver with a FP16 (half precision) preconditioner is developed for a semi-implicit finite difference solver in the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D. In the solver, the bottleneck of global collective communication is resolved using a CA-Krylov subspace method, and halo data communication is reduced by the FP16 preconditioner, which improves the convergence property. The FP16 preconditioner is designed based on the physics properties of the operator and is implemented using the new support for FP16 SIMD operations on A64FX. The solver is ported also on GPUs, and the performance of ITER size simulations with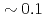 
trillion grids is measured on Fugaku (A64FX) and Summit (V100). The new solver accelerates GT5D by 
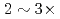from the conventional non-CA solver, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs both on Fugaku and Summit.
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Proceedings of International Conference for High Performance Computing, Networking, Storage, and Analysis (SC 2020) (Internet), p.1318 - 1330, 2020/11
Times Cited Count：2 Percentile：46.63(Computer Science, Information Systems)The multi-scale full-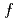
simulation of the next generation experimental fusion reactor ITER based on a five dimensional (5D) gyrokinetic model is one of the most computationally demanding problems in fusion science. In this work, a Gyrokinetic Toroidal 5D Eulerian code (GT5D) is accelerated by a new mixed-precision communication-avoiding (CA) Krylov method. The bottleneck of global collective communication on accelerated computing platforms is resolved using a CA Krylov method. In addition, a new FP16 preconditioner, which is designed using the new support for FP16 SIMD operations on A64FX, reduces both the number of iterations (halo data communication) and the computational cost. The performance of the proposed method for ITER size simulations with 0.1 trillion grids on 1,440 CPUs/GPUs on Fugaku and Summit shows 2.8x and 1.9x speedups respectively from the conventional non-CA Krylov method, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs.
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Proceedings of Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo 2020 (SNA + MC 2020), p.225 - 230, 2020/10
A new communication avoiding (CA) Krylov solver with a FP16 (half precision) preconditioner is developed for a semi-implicit finite difference solver in the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D. In the solver, the bottleneck of global collective communication is resolved using a CA-Krylov subspace method, while the number of halo data communication is reduced by improving the convergence property using the FP16 preconditioner. The FP16 preconditioner is designed based on the physics properties of the operator and is implemented using the new support for FP16 SIMD operations on A64FX. The solver is ported on Fugaku (A64FX) and Summit (V100), which respectively show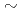 
63x and 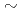29x speedups in socket performance compared to the conventional non-CA Krylov solver on JAEA-ICEX (Haswell).
Idomura, Yasuhiro; Onodera, Naoyuki; Yamada, Susumu; Yamashita, Susumu; Ina, Takuya*; Imamura, Toshiyuki*
Supa Kompyuteingu Nyusu, 22(5), p.18 - 29, 2020/09
A communication avoiding multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against the conventional Krylov methods. The CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with 90 billion DOFs, and its performance is compared against the preconditioned CG solver. In this benchmark, the number of iterations is reduced to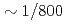 
, and 
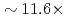speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
Yamada, Susumu; Machida, Masahiko; Imamura, Toshiyuki*
Parallel Computing; Technology Trends, p.105 - 113, 2020/00
Times Cited Count：1 Percentile：29.37(Computer Science, Hardware & Architecture)no abstracts in English
Ali, Y.*; Onodera, Naoyuki; Idomura, Yasuhiro; Ina, Takuya*; Imamura, Toshiyuki*
Proceedings of 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2019), p.1 - 8, 2019/11
Times Cited Count：11 Percentile：93.84(Computer Science, Theory & Methods)Iterative methods for solving large linear systems are common parts of computational fluid dynamics (CFD) codes. The Preconditioned Conjugate Gradient (P-CG) method is one of the most widely used iterative methods. However, in the P-CG method, global collective communication is a crucial bottleneck especially on accelerated computing platforms. To resolve this issue, communication avoiding (CA) variants of the P-CG method are becoming increasingly important. In this paper, the P-CG and Preconditioned Chebyshev Basis CA CG (P-CBCG) solvers in the multiphase CFD code JUPITER are ported to the latest V100 GPUs. All GPU kernels are highly optimized to achieve about 90% of the roofline performance, the block Jacobi preconditioner is re-designed to extract high computing power of GPUs, and the remaining bottleneck of halo data communication is avoided by overlapping communication and computation. The overall performance of the P-CG and P-CBCG solvers is determined by the competition between the CA properties of the global collective communication and the halo data communication, indicating an importance of the inter-node interconnect bandwidth per GPU. The developed GPU solvers are accelerated up to 2x compared with the former CPU solvers on KNLs, and excellent strong scaling is achieved up to 7,680 GPUs on the Summit.
Idomura, Yasuhiro; Ina, Takuya*; Yamashita, Susumu; Onodera, Naoyuki; Yamada, Susumu; Imamura, Toshiyuki*
Proceedings of 9th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2018) (Internet), p.17 - 24, 2018/11
Times Cited Count：8 Percentile：89.56(Computer Science, Theory & Methods)A communication avoiding (CA) multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against CA Krylov methods. In the JUPITER code, the CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with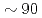 
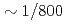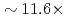billion DOFs, and it is shown that compared with a preconditioned CG solver, the number of iterations is reduced to , and speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu; Imamura, Toshiyuki*
Lecture Notes in Computer Science 10776, p.257 - 273, 2018/00
Times Cited Count：2 Percentile：46.04(Computer Science, Artificial Intelligence)A preconditioned Chebyshev basis communication-avoiding conjugate gradient method (P-CBCG) is applied to the pressure Poisson equation in a multiphase thermal-hydraulic CFD code JUPITER, and its computational performance and convergence properties are compared against a preconditioned conjugate gradient (P-CG) method and a preconditioned communication-avoiding conjugate gradient (P-CACG) method on the Oakforest-PACS, which consists of 8,208 KNLs. The P-CBCG method reduces the number of collective communications with keeping the robustness of convergence properties. Compared with the P-CACG method, an order of magnitude larger communication-avoiding steps are enabled by the improved robustness. It is shown that the P-CBCG method is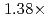 
and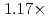 
faster than the P-CG and P-CACG methods at 2,000 processors, respectively.
Yamada, Susumu; Imamura, Toshiyuki*; Machida, Masahiko
Lecture Notes in Computer Science 10776, p.243 - 256, 2018/00
Times Cited Count：1 Percentile：30.96(Computer Science, Artificial Intelligence)no abstracts in English
Yamada, Susumu; Imamura, Toshiyuki*; Machida, Masahiko
Parallel Computing is Everywhere, p.27 - 36, 2018/00
no abstracts in English
Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu; Matsumoto, Kazuya*; Asahi, Yuichi*; Imamura, Toshiyuki*
Proceedings of 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2017), p.7_1 - 7_8, 2017/11
A communication-avoiding generalized minimal residual (CA-GMRES) method is applied to the gyrokinetic toroidal five dimensional Eulerian code GT5D, and its performance is compared against the original code with a generalized conjugate residual (GCR) method on the JAEA ICEX (Haswell), the Plasma Simulator (FX100), and the Oakforest-PACS (KNL). The CA-GMRES method has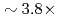 
higher arithmetic intensity than the GCR method, and thus, is suitable for future Exa-scale architectures with limited memory and network bandwidths. In the performance evaluation, it is shown that compared with the GCR solver, its computing kernels are accelerated by 
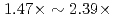, and the cost of data reduction communication is reduced from 
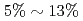to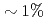 
of the total cost at 1,280 nodes.
Yamada, Susumu; Ina, Takuya*; Sasa, Narimasa; Idomura, Yasuhiro; Machida, Masahiko; Imamura, Toshiyuki*
Proceedings of 2017 IEEE International Parallel & Distributed Processing Symposium Workshops (IPDPSW) (Internet), p.1418 - 1425, 2017/08
Times Cited Count：3 Percentile：56.30(Computer Science, Hardware & Architecture)no abstracts in English
Mayumi, Akie; Idomura, Yasuhiro; Ina, Takuya; Yamada, Susumu; Imamura, Toshiyuki*
Proceedings of 7th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2016) (Internet), p.17 - 24, 2016/11
The left-preconditioned communication avoiding conjugate gradient (LP-CA-CG) method is applied to the pressure Poisson equation in the multiphase CFD code JUPITER. The arithmetic intensity of the LP-CA-CG method is analyzed, and is dramatically improved by loop splitting for inner product operations and for three term recurrence operations. Two LP-CA-CG solvers with block Jacobi preconditioning and with underlap preconditioning are developed. It is shown that on the K computer, the LP-CA-CG solvers with block Jacobi preconditioning is faster, because the performance of local point-to-point communications scales well, and the convergence property becomes worse with underlap preconditioning. The LP-CA-CG solver shows good strong scaling up to 30,000 nodes, where the LP-CA-CG solver achieved higher performance than the original CG solver by reducing the cost of global collective communications by 69%.
Sasa, Narimasa; Yamada, Susumu; Machida, Masahiko; Imamura, Toshiyuki*
Nonlinear Theory and Its Applications, IEICE (Internet), 7(3), p.354 - 361, 2016/07
A round off error accumulation in iterative use of the FFT is discussed. By using numerical simulations of partial differential equations, we numerically show that the round off error in iterative use of the FFT tend to be accumulated. To avoid a lack of precision, we give numerical simulations by using a quadruple precision floating point number, which ensure a sufficient precision against the round off errors by the FFT.
Yamada, Susumu; Imamura, Toshiyuki*; Machida, Masahiko
Parallel Computing; On the Road to Exascale, p.361 - 369, 2016/00
Times Cited Count：1 Percentile：40.54(Computer Science, Hardware & Architecture)no abstracts in English
