Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Onodera, Naoyuki; Sugihara, Kenta; Ina, Takuya; Idomura, Yasuhiro
Keisan Kogaku Koenkai Rombunshu (CD-ROM), 29, 3 Pages, 2024/06
Gas-liquid two-phase flow analysis is one of the most important research topics in nuclear engineering because it is essential for safety evaluation and reactor design. However, it requires large-scale multi-scale simulations, and advanced numerical approaches are needed. To meet this challenge, we have continued to develop the Poisson solver for the multiphase flow analysis code JUPITER. In this study, we aim to improve the convergence of the pressure Poisson solver by formulating the Navier-Stokes equation without using the incompressible approximation. The convergence performance was measured on 8 GPUs for bubbly flow analysis in a circular tube. The results show that the computation time and the number of iterations are reduced by half compared to those using the incompressible approximation, which indicates the usefulness of the formulation in the present study.
Hasegawa, Yuta; Onodera, Naoyuki; Asahi, Yuichi; Ina, Takuya; Imamura, Toshiyuki*; Idomura, Yasuhiro
Fluid Dynamics Research, 55(6), p.065501_1 - 065501_25, 2023/11
Times Cited Count:1 Percentile:13.13(Mechanics)We investigate the applicability of the data assimilation (DA) to large eddy simulations (LESs) based on the lattice Boltzmann method (LBM). We carry out the observing system simulation experiment of a two-dimensional (2D) forced isotropic turbulence, and examine the DA accuracy of the nudging and the local ensemble transform Kalman filter (LETKF) with spatially sparse and noisy observation data of flow fields. The advantage of the LETKF is that it does not require computing spatial interpolation and/or an inverse problem between the macroscopic variables (the density and the pressure) and the velocity distribution function of the LBM, while the nudging introduces additional models for them. The numerical experiments with 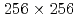 grids and 10% observation noise in the velocity showed that the root mean square error of the velocity in the LETKF with
grids and 10% observation noise in the velocity showed that the root mean square error of the velocity in the LETKF with 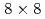 observation points (
observation points (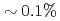 of the total grids) and 64 ensemble members becomes smaller than the observation noise, while the nudging requires an order of magnitude larger number of observation points to achieve the same accuracy. Another advantage of the LETKF is that it well keeps the amplitude of the energy spectrum, while only the phase error becomes larger with more sparse observation. From these results, it was shown that the LETKF enables robust and accurate DA for the 2D LBM with sparse and noisy observation data.
of the total grids) and 64 ensemble members becomes smaller than the observation noise, while the nudging requires an order of magnitude larger number of observation points to achieve the same accuracy. Another advantage of the LETKF is that it well keeps the amplitude of the energy spectrum, while only the phase error becomes larger with more sparse observation. From these results, it was shown that the LETKF enables robust and accurate DA for the 2D LBM with sparse and noisy observation data.
Ina, Takuya; Idomura, Yasuhiro; Imamura, Toshiyuki*; Onodera, Naoyuki
Proceedings of International Conference on High Performance Computing in Asia-Pacific Region (HPC Asia 2023) (Internet), p.29 - 34, 2023/02
Mixed precision Krylov solvers with the Jacobi preconditioner often show significant convergence degradation when the Jacobi preconditioner is computed in low precision such as FP16 and BF16. It is found that this convergence degradation is attributed to loss of diagonal dominance due to roundoff errors in data conversion. To resolve this issue, we propose a new data conversion method, which is designed to keep diagonal dominance of the original matrix data. The proposed method is tested by computing the Poisson equation using the conjugate gradient method, the general minimum residual method, and the biconjugate gradient stabilized method with the FP16/BF16 Jacobi preconditioner on NVIDIA V100 GPUs. Here, the new data conversion is implemented by switching the round-nearest, round-up, round-down, and round-towards-zero intrinsics in CUDA, and is called once before the main iteration. Therefore, the cost of the new data conversion is negligible. When the coefficients of matrix is continuously changed by scaling the linear system, the conventional data conversion based on the round-nearest intrinsic shows periodic changes of the convergence property depending on the difference of the roundoff errors between diagonal and off-diagonal coefficients. Here, the period and magnitude of the convergence degradation depend on the bit length of significand. On the other hand, the proposed data conversion method is shown to fully avoid the convergence degradation, and robust mixed precision computing is enabled for the Jacobi preconditioner without extra overheads.
Hasegawa, Yuta; Imamura, Toshiyuki*; Ina, Takuya; Onodera, Naoyuki; Asahi, Yuichi; Idomura, Yasuhiro
Proceedings of 13th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Heterogeneous Systems (ScalAH22) (Internet), p.10 - 17, 2022/00
The ensemble data assimilation of computational fluid dynamics simulations based on the lattice Boltzmann method (LBM) and the local ensemble transform Kalman filter (LETKF) is implemented and optimized on a GPU supercomputer based on NVIDIA A100 GPUs. To connect the LBM and LETKF parts, data transpose communication is optimized by overlapping computation, file I/O, and communication based on data dependency in each LETKF kernel. In two dimensional forced isotropic turbulence simulations with the ensemble size of 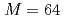 and the number of grid points of
and the number of grid points of 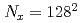 , the optimized implementation achieved
, the optimized implementation achieved 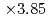 speedup from the naive implementation, in which the LETKF part is not parallelized. The main computing kernel of the local problem is the eigenvalue decomposition (EVD) of
speedup from the naive implementation, in which the LETKF part is not parallelized. The main computing kernel of the local problem is the eigenvalue decomposition (EVD) of 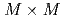 real symmetric dense matrices, which is computed by a newly developed batched EVD in EigenG. The batched EVD in EigenG outperforms that in cuSolver, and
real symmetric dense matrices, which is computed by a newly developed batched EVD in EigenG. The batched EVD in EigenG outperforms that in cuSolver, and 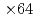 speedup was achieved.
speedup was achieved.
Hayashi, Natsuki*; Matsumura, Daiju; Hoshina, Hiroyuki*; Ueki, Yuji*; Tsuji, Takuya; Chen, J.*; Seko, Noriaki*
Separation and Purification Technology, 277, p.119536_1 - 119536_8, 2021/12
Times Cited Count:26 Percentile:70.03(Engineering, Chemical)Hashimoto, Shoji*; Tanaka, Taku*; Komatsu, Masabumi*; Gonze, M.-A.*; Sakashita, Wataru*; Kurikami, Hiroshi; Nishina, Kazuya*; Ota, Masakazu; Ohashi, Shinta*; Calmon, P.*; et al.
Journal of Environmental Radioactivity, 238-239, p.106721_1 - 106721_10, 2021/11
Times Cited Count:14 Percentile:55.86(Environmental Sciences)This study was aimed at analysing performance of models for radiocesium migration mainly in evergreen coniferous forest in Fukushima, by inter-comparison between models of several research teams. The exercise included two scenarios of countermeasures against the contamination, namely removal of soil surface litter and forest renewal, and a specific konara oak forest scenario in addition to the evergreen forest scenario. All the models reproduced trend of time evolution of radiocesium inventories and concentrations in each of the components in forest such as leaf and organic soil layer. However, the variations between models enlarged in long-term predictions over 50 years after the fallout, meaning continuous field monitoring and model verification/validation is necessary.
Ina, Takuya*; Idomura, Yasuhiro; Imamura, Toshiyuki*; Yamashita, Susumu; Onodera, Naoyuki
Proceedings of 12th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems ScalA21) (Internet), 8 Pages, 2021/11
Times Cited Count:3 Percentile:65.19(Computer Science, Software Engineering)A new mixed-precision preconditioner based on the iterative refinement (IR) method is developed for preconditioned conjugate gradient (P-CG) and multigrid preconditioned conjugate gradient (MGCG) solvers in a multi-phase thermal-hydraulic CFD code JUPITER. In the IR preconditioner, all data is stored in FP16 to reduce memory access, while all computation is performed in FP32. The hybrid FP16/32 implementation keeps the similar convergence property as FP32, while the computational performance is close to FP16. The developed solvers are optimized on Fugaku (A64FX), and applied to ill-conditioned matrices in JUPITER. The P-CG and MGCG solvers with the new IR preconditioner show excellent strong scaling up to 8,000 nodes, and at 8,000 nodes, they are respectively accelerated up to 4.86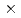 and 2.39
and 2.39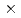 from the conventional ones on Oakforest-PACS (KNL).
from the conventional ones on Oakforest-PACS (KNL).
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Dai-34-Kai Suchi Ryutai Rikigaku Shimpojiumu Koen Rombunshu (Internet), 6 Pages, 2020/12
A new communication avoiding (CA) Krylov solver with a FP16 (half precision) preconditioner is developed for a semi-implicit finite difference solver in the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D. In the solver, the bottleneck of global collective communication is resolved using a CA-Krylov subspace method, and halo data communication is reduced by the FP16 preconditioner, which improves the convergence property. The FP16 preconditioner is designed based on the physics properties of the operator and is implemented using the new support for FP16 SIMD operations on A64FX. The solver is ported also on GPUs, and the performance of ITER size simulations with 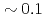 trillion grids is measured on Fugaku (A64FX) and Summit (V100). The new solver accelerates GT5D by
trillion grids is measured on Fugaku (A64FX) and Summit (V100). The new solver accelerates GT5D by 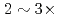 from the conventional non-CA solver, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs both on Fugaku and Summit.
from the conventional non-CA solver, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs both on Fugaku and Summit.
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Proceedings of International Conference for High Performance Computing, Networking, Storage, and Analysis (SC 2020) (Internet), p.1318 - 1330, 2020/11
Times Cited Count:2 Percentile:46.34(Computer Science, Information Systems)The multi-scale full-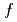 simulation of the next generation experimental fusion reactor ITER based on a five dimensional (5D) gyrokinetic model is one of the most computationally demanding problems in fusion science. In this work, a Gyrokinetic Toroidal 5D Eulerian code (GT5D) is accelerated by a new mixed-precision communication-avoiding (CA) Krylov method. The bottleneck of global collective communication on accelerated computing platforms is resolved using a CA Krylov method. In addition, a new FP16 preconditioner, which is designed using the new support for FP16 SIMD operations on A64FX, reduces both the number of iterations (halo data communication) and the computational cost. The performance of the proposed method for ITER size simulations with 0.1 trillion grids on 1,440 CPUs/GPUs on Fugaku and Summit shows 2.8x and 1.9x speedups respectively from the conventional non-CA Krylov method, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs.
simulation of the next generation experimental fusion reactor ITER based on a five dimensional (5D) gyrokinetic model is one of the most computationally demanding problems in fusion science. In this work, a Gyrokinetic Toroidal 5D Eulerian code (GT5D) is accelerated by a new mixed-precision communication-avoiding (CA) Krylov method. The bottleneck of global collective communication on accelerated computing platforms is resolved using a CA Krylov method. In addition, a new FP16 preconditioner, which is designed using the new support for FP16 SIMD operations on A64FX, reduces both the number of iterations (halo data communication) and the computational cost. The performance of the proposed method for ITER size simulations with 0.1 trillion grids on 1,440 CPUs/GPUs on Fugaku and Summit shows 2.8x and 1.9x speedups respectively from the conventional non-CA Krylov method, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs.
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Proceedings of Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo 2020 (SNA + MC 2020), p.225 - 230, 2020/10
A new communication avoiding (CA) Krylov solver with a FP16 (half precision) preconditioner is developed for a semi-implicit finite difference solver in the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D. In the solver, the bottleneck of global collective communication is resolved using a CA-Krylov subspace method, while the number of halo data communication is reduced by improving the convergence property using the FP16 preconditioner. The FP16 preconditioner is designed based on the physics properties of the operator and is implemented using the new support for FP16 SIMD operations on A64FX. The solver is ported on Fugaku (A64FX) and Summit (V100), which respectively show 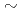 63x and
63x and 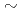 29x speedups in socket performance compared to the conventional non-CA Krylov solver on JAEA-ICEX (Haswell).
29x speedups in socket performance compared to the conventional non-CA Krylov solver on JAEA-ICEX (Haswell).
 Cs tracer
Cs tracerSuzui, Nobuo*; Shibata, Takuya; Yin, Y.-G.*; Funaki, Yoshihito*; Kurita, Keisuke; Hoshina, Hiroyuki*; Yamaguchi, Mitsutaka*; Fujimaki, Shu*; Seko, Noriaki*; Watabe, Hiroshi*; et al.
Scientific Reports (Internet), 10, p.16155_1 - 16155_9, 2020/10
Times Cited Count:2 Percentile:17.49(Multidisciplinary Sciences)Idomura, Yasuhiro; Onodera, Naoyuki; Yamada, Susumu; Yamashita, Susumu; Ina, Takuya*; Imamura, Toshiyuki*
Supa Kompyuteingu Nyusu, 22(5), p.18 - 29, 2020/09
A communication avoiding multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against the conventional Krylov methods. The CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with 90 billion DOFs, and its performance is compared against the preconditioned CG solver. In this benchmark, the number of iterations is reduced to 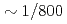 , and
, and 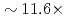 speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
Matsumoto, Kazuya*; Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu
Journal of Supercomputing, 75(12), p.8115 - 8146, 2019/12
Times Cited Count:2 Percentile:20.81(Computer Science, Hardware & Architecture)A communication-avoiding generalized minimum residual method (CA-GMRES) is implemented on a hybrid CPU-GPU cluster, targeted for the performance acceleration of iterative linear system solver in the gyrokinetic toroidal five-dimensional Eulerian code GT5D. In addition to the CA-GMRES, we implement and evaluate a modified variant of CA-GMRES (M-CA-GMRES) proposed in our previous study to reduce the amount of floating-point calculations. This study demonstrates that beneficial features of the CA-GMRES are in its minimum number of collective communications and its highly efficient calculations based on dense matrix-matrix operations. The performance evaluation is conducted on the Reedbush-L GPU cluster, which contains four NVIDIA Tesla P100 GPUs per compute node. The evaluation results show that the M-CA-GMRES is 1.09x, 1.22x and 1.50x faster than the CA-GMRES, the generalized conjugate residual method (GCR), and the GMRES, respectively, when 64 GPUs are used.
Ali, Y.*; Onodera, Naoyuki; Idomura, Yasuhiro; Ina, Takuya*; Imamura, Toshiyuki*
Proceedings of 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2019), p.1 - 8, 2019/11
Times Cited Count:11 Percentile:93.69(Computer Science, Theory & Methods)Iterative methods for solving large linear systems are common parts of computational fluid dynamics (CFD) codes. The Preconditioned Conjugate Gradient (P-CG) method is one of the most widely used iterative methods. However, in the P-CG method, global collective communication is a crucial bottleneck especially on accelerated computing platforms. To resolve this issue, communication avoiding (CA) variants of the P-CG method are becoming increasingly important. In this paper, the P-CG and Preconditioned Chebyshev Basis CA CG (P-CBCG) solvers in the multiphase CFD code JUPITER are ported to the latest V100 GPUs. All GPU kernels are highly optimized to achieve about 90% of the roofline performance, the block Jacobi preconditioner is re-designed to extract high computing power of GPUs, and the remaining bottleneck of halo data communication is avoided by overlapping communication and computation. The overall performance of the P-CG and P-CBCG solvers is determined by the competition between the CA properties of the global collective communication and the halo data communication, indicating an importance of the inter-node interconnect bandwidth per GPU. The developed GPU solvers are accelerated up to 2x compared with the former CPU solvers on KNLs, and excellent strong scaling is achieved up to 7,680 GPUs on the Summit.
Idomura, Yasuhiro; Ina, Takuya*; Yamashita, Susumu; Onodera, Naoyuki; Yamada, Susumu; Imamura, Toshiyuki*
Proceedings of 9th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2018) (Internet), p.17 - 24, 2018/11
Times Cited Count:8 Percentile:89.41(Computer Science, Theory & Methods)A communication avoiding (CA) multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against CA Krylov methods. In the JUPITER code, the CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with 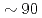 billion DOFs, and it is shown that compared with a preconditioned CG solver, the number of iterations is reduced to
billion DOFs, and it is shown that compared with a preconditioned CG solver, the number of iterations is reduced to 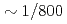 , and
, and 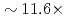 speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
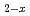 Ce
Ce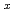 CuO
CuO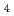 studied by Cu
studied by Cu 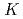 -edge X-ray absorption spectroscopy
-edge X-ray absorption spectroscopyAsano, Shun*; Ishii, Kenji*; Matsumura, Daiju; Tsuji, Takuya; Ina, Toshiaki*; Suzuki, Kensuke*; Fujita, Masaki*
Journal of the Physical Society of Japan, 87(9), p.094710_1 - 094710_5, 2018/09
Times Cited Count:13 Percentile:62.91(Physics, Multidisciplinary)Seko, Noriaki*; Hoshina, Hiroyuki*; Kasai, Noboru*; Shibata, Takuya; Saiki, Seiichi*; Ueki, Yuji*
Radiation Physics and Chemistry, 143, p.33 - 37, 2018/02
Times Cited Count:19 Percentile:84.57(Chemistry, Physical)Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu; Imamura, Toshiyuki*
Lecture Notes in Computer Science 10776, p.257 - 273, 2018/00
Times Cited Count:3 Percentile:45.87(Computer Science, Artificial Intelligence)A preconditioned Chebyshev basis communication-avoiding conjugate gradient method (P-CBCG) is applied to the pressure Poisson equation in a multiphase thermal-hydraulic CFD code JUPITER, and its computational performance and convergence properties are compared against a preconditioned conjugate gradient (P-CG) method and a preconditioned communication-avoiding conjugate gradient (P-CACG) method on the Oakforest-PACS, which consists of 8,208 KNLs. The P-CBCG method reduces the number of collective communications with keeping the robustness of convergence properties. Compared with the P-CACG method, an order of magnitude larger communication-avoiding steps are enabled by the improved robustness. It is shown that the P-CBCG method is 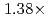 and
and 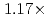 faster than the P-CG and P-CACG methods at 2,000 processors, respectively.
faster than the P-CG and P-CACG methods at 2,000 processors, respectively.
Yamashita, Susumu; Ina, Takuya*; Idomura, Yasuhiro; Yoshida, Hiroyuki
Dai-31-Kai Suchi Ryutai Rikigaku Shimpojiumu Koen Rombunshu (DVD-ROM), 7 Pages, 2017/12
no abstracts in English
Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu; Matsumoto, Kazuya*; Asahi, Yuichi*; Imamura, Toshiyuki*
Proceedings of 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2017), p.7_1 - 7_8, 2017/11
A communication-avoiding generalized minimal residual (CA-GMRES) method is applied to the gyrokinetic toroidal five dimensional Eulerian code GT5D, and its performance is compared against the original code with a generalized conjugate residual (GCR) method on the JAEA ICEX (Haswell), the Plasma Simulator (FX100), and the Oakforest-PACS (KNL). The CA-GMRES method has 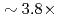 higher arithmetic intensity than the GCR method, and thus, is suitable for future Exa-scale architectures with limited memory and network bandwidths. In the performance evaluation, it is shown that compared with the GCR solver, its computing kernels are accelerated by
higher arithmetic intensity than the GCR method, and thus, is suitable for future Exa-scale architectures with limited memory and network bandwidths. In the performance evaluation, it is shown that compared with the GCR solver, its computing kernels are accelerated by 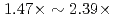 , and the cost of data reduction communication is reduced from
, and the cost of data reduction communication is reduced from 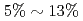 to
to 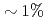 of the total cost at 1,280 nodes.
of the total cost at 1,280 nodes.