Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Fujii, Daisuke; Iwanaka, Akihiro*; Kitazawa, Masakiyo*; Suenaga, Daiki*
Physical Review D, 110(9), p.094016_1 - 094016_16, 2024/11
We investigate the thermodynamics and phase structure of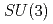 
Yang-Mills theory on 
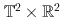in Euclidean spacetime in an effective-model approach. The model incorporates two Polyakov loops along two compactified directions as dynamical variables, and is constructed to reproduce thermodynamics on 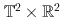measured on the lattice. The model analysis indicates the existence of a novel first-order phase transition on 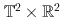in the deconfined phase, which terminates at critical points that should belong to the two-dimensional 
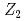universality class. We argue that the interplay of the Polyakov loops induced by their cross term in the Polyakov-loop potential is responsible for the manifestation of the first-order transition.
Sako, Hiroyuki; Harada, Hiroyuki; Sakaguchi, Takao*; Chujo, Tatsuya*; Esumi, Shinichi*; Gunji, Taku*; Hasegawa, Shoichi; Hwang, S.; Ichikawa, Yudai; Imai, Kenichi; et al.
Nuclear Physics A, 956, p.850 - 853, 2016/12
Times Cited Count：13 Percentile：66.42(Physics, Nuclear)
Fujii, Daisuke; Iwanaka, Akihiro*; Suenaga, Daiki*; Kitazawa, Masakiyo*
no journal, ,
The Matsubara formalism for the thermal quantum field theory introduces temperature into the theory as a boundary condition along the imaginary time direction of Euclidean spacetime. In this study, we consider the pure Yang-Mills theory on 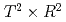, which further imposes boundary conditions on the spatial direction, and discuss thermodynamic quantities and phase structures. Results from lattice QCD simulations show that anisotropic effects are suppressed until the spatial directional spread becomes significantly smaller near the critical temperature. By constructing the model to reproduce the lattice QCD results, it becomes clear that the system suggests the existence of a very rich phase structure.
Fujii, Daisuke; Iwanaka, Akihiro*; Suenaga, Daiki*; Kitazawa, Masakiyo*
no journal, ,
The Matsubara formalism for the thermal quantum field theory introduces temperature into the theory as a boundary condition along the imaginary time direction of Euclidean spacetime. In this study, we further consider the pure Yang-Mills theory on 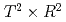with boundary conditions in one spatial direction, and discuss thermodynamic quantities and their phase structures. The introducing of the boundary condition leads to the breaking of rotational symmetry, which results in anisotropy of the pressure. Results from lattice QCD simulations show that the anisotropic effect is suppressed until the spatial spread becomes significantly smaller near the critical temperature. This result is a very different behavior from that of free-particle systems. In order to reveal the mechanism behind this result, we employ an effective model with two Polyakov loops along the time and spatial directions. We show that introducing the competition between the two Polyakov loops as suggested in a previous study describes well the lattice data in the high temperature region. Furthermore, we show that a new first-order phase transition is suggested, which is different from the confinement phase transition.
Fujii, Daisuke; Iwanaka, Akihiro*; Suenaga, Daiki*; Kitazawa, Masakiyo*
no journal, ,
We discuss pure Yang-Mills theory with anisotropic boundary conditions on 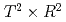manifolds. The lattice QCD results show that anisotropy effects are suppressed until the spatial spread becomes significantly smaller near the critical temperature. We successfully reproduce the thermodynamics of lattice by extending the Polyakov loop model, which describes the usual finite temperature, on 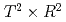with parameters. Furthermore, by considering the physical background, we show that the competition between the two Polyakov loops introduced in the model and the existence of a new first-order phase transition are important.
Fujii, Daisuke; Iwanaka, Akihiro*; Suenaga, Daiki*; Kitazawa, Masakiyo*
no journal, ,
We consider a pure Yang-Mills theory on 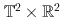with boundary conditions imposed not only in the imaginary time direction but also in one spatial direction, and discuss thermodynamic quantities and their phase structures. The introduction of the boundary condition leads to the breaking of rotational symmetry, resulting in anisotropy of the pressure. Results from lattice QCD simulations show that the anisotropic effect is suppressed until the spatial extension becomes significantly smaller near the critical temperature. This result is a very different behavior from that of massless free boson systems. In order to clarify the mechanism behind this result, we employ an effective model with two Polyakov loops along the time and spatial directions. We show that introducing the interplay of two Polyakov loops well describes the lattice data in the high-temperature region, as suggested in a previous study. Furthermore, we suggest the presence of a new first-order phase transition, which is distinguished from the confinement phase transition.
