Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
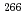 Bh in the
Bh in the 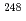 Cm(
Cm(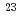 Na,5
Na,5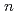 )
)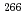 Bh reaction and its decay properties
Bh reaction and its decay propertiesHaba, Hiromitsu*; Fan, F.*; Kaji, Daiya*; Kasamatsu, Yoshitaka*; Kikunaga, Hidetoshi*; Komori, Yukiko*; Kondo, Narumi*; Kudo, Hisaaki*; Morimoto, Koji*; Morita, Kosuke*; et al.
Physical Review C, 102(2), p.024625_1 - 024625_12, 2020/08
Times Cited Count:7 Percentile:55.09(Physics, Nuclear)Seguchi, Tadao*; Tamura, Kiyotoshi*; Kudo, Hisaaki*; Shimada, Akihiko; Sugimoto, Masaki
IEEE Transactions on Dielectrics and Electrical Insulation, 22(6), p.3197 - 3206, 2015/12
Times Cited Count:30 Percentile:76.05(Engineering, Electrical & Electronic)The degradation of ethylene propylene rubber (EPR) sheets as a cable insulation material for nuclear power plants (NPP) was studied by accelerated thermal ageing, radiation ageing and thermal - radiation combined ageing. The oxidation of EPR proceeded with ageing and the decay of mechanical property was closely related to the content of oxidation products. The antioxidant as a stabilizer in EPR was effective for the thermal oxidation, but not for the radiation oxidation. For the thermal and radiation combined oxidation, the mechanical property and the content of oxidation products were different among the treatment sequences due to the decay of antioxidant. The lifetime of EPR cable is closely related to the remaining content of antioxidant, and the lifetime evaluation would be recommended by the reverse sequential combination (thermal ageing after radiation ageing).
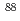 Nb and
Nb and 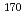 Ta for chemical studies of element 105, Db, using the GARIS gas-jet system
Ta for chemical studies of element 105, Db, using the GARIS gas-jet systemHuang, M.*; Haba, Hiromitsu*; Murakami, Masashi*; Asai, Masato; Kaji, Daiya*; Kanaya, Jumpei*; Kasamatsu, Yoshitaka*; Kikunaga, Hidetoshi*; Kikutani, Yuki*; Komori, Yukiko*; et al.
Journal of Radioanalytical and Nuclear Chemistry, 304(2), p.845 - 849, 2015/05
Times Cited Count:3 Percentile:23.43(Chemistry, Analytical)A technique to utilize radioisotopes of Nb and Ta was developed for chemical studies of element 105, Db, by coupling a gas-jet transport system to the RIKEN gas-filled recoil ion separator (GARIS). The short-lived 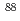 Nb and
Nb and 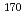 Ta were produced with nuclear reactions using a
Ta were produced with nuclear reactions using a 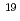 F beam whose energy was the same as that to produce
F beam whose energy was the same as that to produce 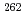 Db. Then, they were separated with GARIS and extracted to a chemistry laboratory with the gas-jet transport system. By changing only magnetic field of GARIS and inserting an energy degrader and a shutter for recoil ions, we could deliver the
Db. Then, they were separated with GARIS and extracted to a chemistry laboratory with the gas-jet transport system. By changing only magnetic field of GARIS and inserting an energy degrader and a shutter for recoil ions, we could deliver the 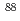 Nb and
Nb and 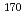 Ta to a chemistry device for
Ta to a chemistry device for 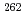 Db without changing other experimental conditions.
Db without changing other experimental conditions.
Shimada, Akihiko; Sugimoto, Masaki; Kudo, Hisaaki*; Tamura, Kiyotoshi*; Seguchi, Tadao*
IEEE Transactions on Dielectrics and Electrical Insulation, 21(1), p.16 - 23, 2014/02
The thermal and radiation ageing behaviors and degradation mechanisms of SiR for the cable insulation of nuclear power plants were studied. The thermal ageing and radiation ageing in air were conducted up to 235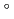 C and 195
C and 195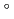 C, respectively. The dose rate of radiation ageing is 1 kGy/h. Thermal ageing in vacuum as well as in air was also conducted. The degraded SiR is evaluated by tensile test, gel fraction measurement, swelling ratio measurement and weight measurement, and then the results are analyzed. It is appeared that the radiation degradation of SiR at high temperature is much more severe than that of SiR at low temperature at the same dose. Focusing on the molecular structure, it is supposed that crosslinking reagents which are included in SiR are removed, oxygen atom is attached instead of the reagents and new crosslinking is foamed. Their behaviors are different from the polymer of hydrocarbon.
C, respectively. The dose rate of radiation ageing is 1 kGy/h. Thermal ageing in vacuum as well as in air was also conducted. The degraded SiR is evaluated by tensile test, gel fraction measurement, swelling ratio measurement and weight measurement, and then the results are analyzed. It is appeared that the radiation degradation of SiR at high temperature is much more severe than that of SiR at low temperature at the same dose. Focusing on the molecular structure, it is supposed that crosslinking reagents which are included in SiR are removed, oxygen atom is attached instead of the reagents and new crosslinking is foamed. Their behaviors are different from the polymer of hydrocarbon.
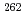 Db in the
Db in the 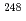 Cm(
Cm(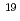 F,5
F,5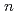 )
)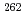 Db reaction and decay properties of
Db reaction and decay properties of 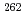 Db and
Db and 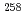 Lr
LrHaba, Hiromitsu*; Huang, M.*; Kaji, Daiya*; Kanaya, Jumpei*; Kudo, Yuki*; Morimoto, Koji*; Morita, Kosuke*; Murakami, Masashi*; Ozeki, Kazutaka*; Sakai, Ryutaro*; et al.
Physical Review C, 89(2), p.024618_1 - 024618_11, 2014/02
Times Cited Count:27 Percentile:81.83(Physics, Nuclear)Shimada, Akihiko; Sugimoto, Masaki; Kudo, Hisaaki*; Tamura, Kiyotoshi*; Seguchi, Tadao*
IEEE Transactions on Dielectrics and Electrical Insulation, 20(6), p.2107 - 2116, 2013/12
Times Cited Count:45 Percentile:84.16(Engineering, Electrical & Electronic)The degradation of cables by the accelerated thermal and radiation ageing for nuclear power plant was studied. The thermal oxidation of crosslinked polyethylene (XLPE) as a cable insulation showed the heterogeneous features along the depth of sheet specimens. The degree of oxidation was closely related to the distribution of antioxidant content due to the decay of antioxidant content by the evaporation and radiation decomposition during accelerated ageing. The specific relations were observed between the tensile properties and the yield of oxidation products and also between the oxidation products and antioxidant content in XLPE specimens. The yields and the content and their distribution were detected by FTIR. The oxidation of XLPE containing antioxidant of enough content proceeded proportionally with ageing time or radiation dose at any ageing conditions. When the antioxidant content decreased less than a limited content by thermal and/or radiation ageing, the oxidation rate by thermal ageing increased sharply with ageing time. Therefore, the oxidation at surface of XLPE was much accelerated when the antioxidant decreased to result the heterogeneous oxidation. The mechanical properties depend closely on the degree of oxidation at the surface. The behavior of oxidation was also affected by the types of antioxidant.
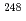 Cm +
Cm + 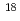 O reaction
O reactionMurakami, Masashi*; Goto, Shinichi*; Murayama, Hirofumi*; Kojima, Takayuki*; Kudo, Hisaaki*; Kaji, Daiya*; Morimoto, Koji*; Haba, Hiromitsu*; Kudo, Yuki*; Sumita, Takayuki*; et al.
Physical Review C, 88(2), p.024618_1 - 024618_8, 2013/08
Times Cited Count:18 Percentile:71.33(Physics, Nuclear)Production cross sections of Rf isotopes in the 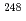 Cm +
Cm + 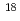 O reaction were measured at the beam energy range of 88.2 to 101.3 MeV by use of a gas-filled recoil ion separator. The excitation functions of
O reaction were measured at the beam energy range of 88.2 to 101.3 MeV by use of a gas-filled recoil ion separator. The excitation functions of 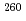 Rf,
Rf, 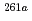 Rf, and
Rf, and 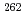 Rf were obtained together with those of spontaneously fissioning nuclides which have few-second half-lives and have been assigned to
Rf were obtained together with those of spontaneously fissioning nuclides which have few-second half-lives and have been assigned to 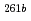 Rf and a longer-lived state of
Rf and a longer-lived state of 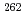 Rf. The excitation function of few-second spontaneously fissioning nuclide exhibited the maximum cross section at the
Rf. The excitation function of few-second spontaneously fissioning nuclide exhibited the maximum cross section at the 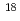 O beam energy of 94.8 MeV. The shape of the excitation function was almost the same as that of
O beam energy of 94.8 MeV. The shape of the excitation function was almost the same as that of 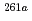 Rf, whereas it was quite different from those of
Rf, whereas it was quite different from those of 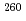 Rf and
Rf and 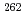 Rf. A few-second spontaneously fissioning nuclide previously reported as
Rf. A few-second spontaneously fissioning nuclide previously reported as 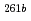 Rf and
Rf and 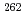 Rf observed in
Rf observed in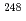 Cm +
Cm + 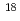 O reaction was identified as
O reaction was identified as 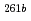 Rf.
Rf.
Sugimoto, Masaki; Shimada, Akihiko; Kudo, Hisaaki*; Tamura, Kiyotoshi; Seguchi, Tadao*
Radiation Physics and Chemistry, 82, p.69 - 73, 2013/01
Times Cited Count:68 Percentile:97.60(Chemistry, Physical)The oxidation products formed by thermal and radiation ageing of crosslinked polyethylene for cable insulation were analyzed by FTIR-ATR spectrometry. The most of products were composed of carboxylic acid, carboxylic ester, and carboxylic anhydride. The carboxylic acid was the primal product, and the others were the secondary products by the thermal reaction of carboxylic acids. The carboxylic acid as the primal oxidation product supports the proposed new oxidation mechanisms that the main chain scission should occur directly by oxidation of polyethylene radicals.
Seguchi, Tadao*; Tamura, Kiyotoshi*; Watashi, Katsumi; Suzuki, Masahide; Shimada, Akihiko; Sugimoto, Masaki; Idesaki, Akira; Yoshikawa, Masahito; Oshima, Takeshi; Kudo, Hisaaki*
JAEA-Research 2012-029, 158 Pages, 2012/12
The degradation mechanisms of ethylene-propylene rubber (EPR), crosslinked polyethylene (XLPE), polyvinylchloride (PVC), and silicone rubber (SiR) as the cable insulation materials were investigated for the cable ageing research of the nuclear power plant. The materials as same insulations for the practical cable (practical formulation) and as the model formulation containing specific additive were selected. They were exposed to the accelerated radiation and thermal environments. The mechanical properties, the crosslinking and chain scission, and the distribution of antioxidant and of oxidative products were measured and analyzed.
Seguchi, Tadao*; Tamura, Kiyotoshi; Shimada, Akihiko; Sugimoto, Masaki; Kudo, Hisaaki*
Radiation Physics and Chemistry, 81(11), p.1747 - 1751, 2012/11
Times Cited Count:49 Percentile:95.12(Chemistry, Physical)The mechanism of polymer oxidation by radiation and thermal ageing was investigated for the life evaluation of cables installed in radiation environments. The antioxidant as a stabilizer was much effective for thermal oxidation with a small content in polymers, but was not effective for radiation oxidation. The ionizing radiation induced the oxidation to result chain scission even at low temperature, because the free radicals were produced and the antioxidant could not stop the oxidation of radicals with the chain scission. A new mechanism of antioxidant effect for polymer oxidation was proposed. The effect of antioxidant was not the termination of free radicals in polymer chains such as peroxy radicals, but was the depression of initial radical formation in polymer chains by thermal activation. The antioxidant molecule was assumed to delocalize the activated energy in polymer chains by Boltzmann statics (distribution) to result decrease the probability of radical formation at a given temperature. The interaction distance (delocalization area) by one antioxidant molecule was estimated to be 5-10 nm in polymer matrix, though the value would depend on the chemical structure of antioxidant.
Shimada, Akihiko; Sugimoto, Masaki; Kudo, Hisaaki*; Tamura, Kiyotoshi; Seguchi, Tadao*
IEEE Transactions on Dielectrics and Electrical Insulation, 19(5), p.1768 - 1773, 2012/10
Times Cited Count:19 Percentile:65.39(Engineering, Electrical & Electronic)The life of cables installed in nuclear power plant was evaluated by the accelerated ageing tests of thermal and radiation degradation. For radiation degradation, the dose rate was the important points, because the oxidation distribution in the insulation was much affected by dose rate due to oxygen penetration limitation during irradiation. The oxidation distribution was observed by FTIR for crosslinked polyethylene (XLPE) and ethylene propylene rubber (EPR) of cable insulation degraded at various irradiation conditions and compared with the mechanical degradation. The oxidation profile was almost same between a low dose rate at room temperature and a high dose rate at elevated temperature (100 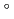 C), and the degradation was same for both irradiations. By increasing the irradiation temperature the oxygen penetration rate increased exponentially and the thermal degradation during irradiation was negligible at around 100
C), and the degradation was same for both irradiations. By increasing the irradiation temperature the oxygen penetration rate increased exponentially and the thermal degradation during irradiation was negligible at around 100 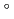 C. Therefore, the dose rate could be increased by 15 times by irradiation at 100
C. Therefore, the dose rate could be increased by 15 times by irradiation at 100 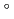 C instead of the irradiation at room temperature for the adequate oxidation throughout insulation. The experimental result was coincident with the theoretical analysis.
C instead of the irradiation at room temperature for the adequate oxidation throughout insulation. The experimental result was coincident with the theoretical analysis.
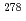 113 of the 113th element
113 of the 113th elementMorita, Kosuke*; Morimoto, Koji*; Kaji, Daiya*; Haba, Hiromitsu*; Ozeki, Kazutaka*; Kudo, Yuki*; Sumita, Takayuki*; Wakabayashi, Yasuo*; Yoneda, Akira*; Tanaka, Kengo*; et al.
Journal of the Physical Society of Japan, 81(10), p.103201_1 - 103201_4, 2012/10
Times Cited Count:179 Percentile:97.24(Physics, Multidisciplinary)An isotope of the 113th element, 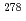 113, was produced in a nuclear reaction with a
113, was produced in a nuclear reaction with a 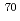 Zn beam on a
Zn beam on a 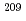 Bi target. We observed six consecutive
Bi target. We observed six consecutive 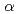 decays following the implantation of a heavy particle in nearly the same position in the semiconductor detector, in extremely low background condition. The fifth and sixth decays are fully consistent with the sequential decays of
decays following the implantation of a heavy particle in nearly the same position in the semiconductor detector, in extremely low background condition. The fifth and sixth decays are fully consistent with the sequential decays of 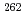 Db and
Db and 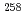 Lr both in decay energies and decay times. This indicates that the present decay chain consisted of
Lr both in decay energies and decay times. This indicates that the present decay chain consisted of 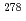 113,
113, 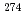 Rg (Z = 111),
Rg (Z = 111), 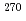 Mt (Z = 109),
Mt (Z = 109), 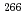 Bh (Z = 107),
Bh (Z = 107), 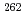 Db (Z = 105), and
Db (Z = 105), and 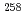 Lr (Z = 103) with firm connections. This result, together with previously reported results from 2004 and 2007, conclusively leads the unambiguous production and identification of the isotope
Lr (Z = 103) with firm connections. This result, together with previously reported results from 2004 and 2007, conclusively leads the unambiguous production and identification of the isotope 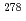 113, of the 113th element.
113, of the 113th element.
Seguchi, Tadao*; Tamura, Kiyotoshi; Kudo, Hisaaki*; Shimada, Akihiko; Sugimoto, Masaki; Idesaki, Akira; Oshima, Takeshi; Yoshikawa, Masahito
JAEA-Review 2012-027, 46 Pages, 2012/08
The research on cable degradation mechanisms was conducted for 5 years in 2006 - 2010 as the project research of plant life management for nuclear power plant by NISA (Nuclear and Industrial Safety Agency) of METI (Ministry of Economy, Trade, and Industry). At the finish of above research, the degradation mechanisms were reviewed on the analysis of many reports on cable degradation. The reports published after 1970 were mainly surveyed and the facts or data containing the experimental accuracy were selected. The verified facts, the reasonable interpretation of the facts, unresolved aspects were checked on the view points of recent techniques or analysis, and proposed the new model of degradation mechanisms was proposed.
 SO
SO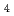 /HNO
/HNO mixed solution
mixed solutionLi, Z.*; Toyoshima, Atsushi; Asai, Masato; Tsukada, Kazuaki; Sato, Tetsuya; Sato, Nozomi; Kikuchi, Takahiro; Nagame, Yuichiro; Sch del, M.; Pershina, V.*; et al.
del, M.; Pershina, V.*; et al.
Radiochimica Acta, 100(3), p.157 - 164, 2012/03
Times Cited Count:14 Percentile:68.81(Chemistry, Inorganic & Nuclear)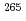 Sg in the
Sg in the 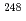 Cm(
Cm(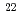 Ne,5
Ne,5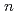 )
)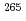 Sg reaction and decay properties of two isomeric states in
Sg reaction and decay properties of two isomeric states in 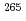 Sg
SgHaba, Hiromitsu*; Kaji, Daiya*; Kudo, Yuki*; Morimoto, Koji*; Morita, Kosuke*; Ozeki, Kazutaka*; Sakai, Ryutaro*; Sumita, Takayuki*; Yoneda, Akira*; Kasamatsu, Yoshitaka*; et al.
Physical Review C, 85(2), p.024611_1 - 024611_11, 2012/02
Times Cited Count:56 Percentile:91.18(Physics, Nuclear)Two isomeric states in 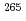 Sg, i.e,
Sg, i.e, 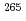 Sg
Sg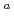 and
and 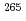 Sg
Sg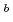 were produced in the
were produced in the 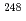 Cm(
Cm(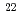 Ne,5
Ne,5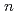 ) reaction. Decay properties of
) reaction. Decay properties of 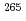 Sg
Sg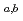 were investigated with a rotating-wheel apparatus for
were investigated with a rotating-wheel apparatus for 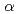 and spontaneous fission (SF) spectrometry under low background condition attained by a gas-jet transport system coupled to the RIKEN gas-filled recoil ion separator. Based on genetically correlated
and spontaneous fission (SF) spectrometry under low background condition attained by a gas-jet transport system coupled to the RIKEN gas-filled recoil ion separator. Based on genetically correlated 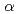 -
-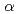 (-
(-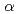 ) and
) and 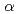 -SF decay chains, 18 and 24 events were assigned to
-SF decay chains, 18 and 24 events were assigned to 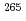 Sg
Sg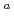 and
and 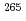 Sg
Sg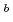 , respectively. The half-life and
, respectively. The half-life and 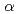 -particle energy of
-particle energy of 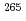 Sg
Sg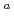 were measured to be
were measured to be 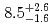 s and
s and 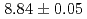 MeV, respectively, and those of
MeV, respectively, and those of 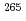 Sg
Sg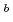 were
were 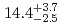 s and
s and 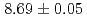 MeV.
MeV.
Ishii, Yasuo; Toyoshima, Atsushi; Tsukada, Kazuaki; Asai, Masato; Li, Z.*; Nagame, Yuichiro; Miyashita, Sunao*; Mori, Tomotaka*; Suganuma, Hideo*; Haba, Hiromitsu*; et al.
Bulletin of the Chemical Society of Japan, 84(9), p.903 - 911, 2011/09
Times Cited Count:18 Percentile:49.57(Chemistry, Multidisciplinary)The cation-exchange behavior of element 104, rutherfordium (Rf), was investigated together with its lighter group-4 homologues Zr and Hf, and the tetravalent pseudo-homologue Th in HF/HNO mixed solution. The results demonstrate that distribution coefficients (
mixed solution. The results demonstrate that distribution coefficients (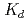 ) of Rf in HF/0.10 M HNO
) of Rf in HF/0.10 M HNO decrease with increasing concentration of the fluoride ion [F
decrease with increasing concentration of the fluoride ion [F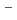 ], indicating the consecutive formation of fluorido complexes of Rf. We also measured the
], indicating the consecutive formation of fluorido complexes of Rf. We also measured the 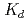 values of Rf and the homologues as a function of the hydrogen ion concentration [H
values of Rf and the homologues as a function of the hydrogen ion concentration [H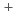 ]. The log
]. The log 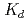 values decrease linearly with an increase of log [H
values decrease linearly with an increase of log [H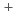 ] with slopes between -2.1 and -2.5. This indicates that these elements are likely to form the same chemical compounds: mixture of [MF]
] with slopes between -2.1 and -2.5. This indicates that these elements are likely to form the same chemical compounds: mixture of [MF]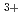 and [MF
and [MF ]
]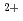 (M = Rf, Zr, Hf and Th) in the studied solution. It is also ascertained that sequence in the fluoride complex formation is Zr
(M = Rf, Zr, Hf and Th) in the studied solution. It is also ascertained that sequence in the fluoride complex formation is Zr 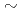 Hf
Hf 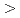 Rf
Rf 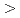 Th.
Th.
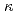 -carrageenan oligomers as plant growth promoter
-carrageenan oligomers as plant growth promoterAbad, L.*; Saiki, Seiichi; Nagasawa, Naotsugu; Kudo, Hisaaki*; Katsumura, Yosuke*; Dela Rosa, A. M.*
Radiation Physics and Chemistry, 80(9), p.977 - 982, 2011/09
Times Cited Count:19 Percentile:77.08(Chemistry, Physical)The optimum molecular weight of irradiated 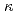 -carrageenan for the plant growth promoting effect is known to be around 10 kDa, which is obtained by irradiation at doses of 100 kGy in solid and of 2 kGy in 1% aqueous solution. In this study, isolated fraction by membrane filter of irradiated
-carrageenan for the plant growth promoting effect is known to be around 10 kDa, which is obtained by irradiation at doses of 100 kGy in solid and of 2 kGy in 1% aqueous solution. In this study, isolated fraction by membrane filter of irradiated 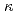 -carrageenan was analyzed by NMR. The chemical shifts of
-carrageenan was analyzed by NMR. The chemical shifts of 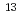 C and
C and 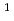 H spectra at the range of 3-10 kDa indicated that the basic functional structure of
H spectra at the range of 3-10 kDa indicated that the basic functional structure of 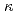 -carrageenan (alternating D-galactose-4-sulfate and 3,6-anhydro-D-galactose dimer) remains intact. No radiolytic product having carbonyl groups was detected at the range of 3-10 kDa, and moved to less than 3 kDa probably. From these results, it is assumed that the plant growth promoting effect of irradiated
-carrageenan (alternating D-galactose-4-sulfate and 3,6-anhydro-D-galactose dimer) remains intact. No radiolytic product having carbonyl groups was detected at the range of 3-10 kDa, and moved to less than 3 kDa probably. From these results, it is assumed that the plant growth promoting effect of irradiated 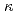 -carrageenan depends on the molecular weight, its intact structure, and not on the radiolytic products.
-carrageenan depends on the molecular weight, its intact structure, and not on the radiolytic products.
Shiraki, Fumiya*; Yoshikawa, Taeko*; Oshima, Akihiro*; Oshima, Yuji*; Takasawa, Yuya*; Fukutake, Naoyuki*; Oyama, Tomoko*; Urakawa, Tatsuya*; Fujita, Hajime*; Takahashi, Tomohiro*; et al.
Nuclear Instruments and Methods in Physics Research B, 269(15), p.1777 - 1781, 2011/08
Times Cited Count:8 Percentile:51.22(Instruments & Instrumentation)The graded energy deposition of heavy ion beam irradiation to polymeric materials was utilized to synthesize a novel proton exchange membrane (PEM) with the graded density of sulfonic acid groups toward the thickness direction. Stacked Poly(tetrafluoroethylene-co-hexafluoropropylene) (FEP) films were irradiated by Xe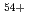 ion beam with the energy of 6 MeV/u under a vacuum condition. Irradiated films were grafted with styrene monomer and then sulfonated. The membrane electrode assembly (MEA) fabricated by the function graded PEM showed improved fuel cell performance in terms of voltage stability. It was expected that the function-graded PEM could control the graded concentration of sulfonic acid groups in PEM.
ion beam with the energy of 6 MeV/u under a vacuum condition. Irradiated films were grafted with styrene monomer and then sulfonated. The membrane electrode assembly (MEA) fabricated by the function graded PEM showed improved fuel cell performance in terms of voltage stability. It was expected that the function-graded PEM could control the graded concentration of sulfonic acid groups in PEM.
Shimada, Akihiko; Kudo, Hisaaki*; Idesaki, Akira; Sugimoto, Masaki; Yoshikawa, Masahito; Tamura, Kiyotoshi; Seguchi, Tadao*
Proceedings of 12th International Conference on Radiation Curing in Asia (RadTech Asia 2011) (Internet), p.244 - 247, 2011/06
Seguchi, Tadao*; Tamura, Kiyotoshi; Oshima, Takeshi; Shimada, Akihiko; Kudo, Hisaaki*
Radiation Physics and Chemistry, 80(2), p.268 - 273, 2011/02
Times Cited Count:70 Percentile:97.60(Chemistry, Physical)The cables applied in radiation facility such as a nuclear power plant degrade by radiation and thermal combined ageing. The degradation of polymers for cable insulation is induced by oxidation, and the oxidation is accelerated by synergism of radiation and thermal oxidation. The degradation mechanisms were studied at accelerated degradation for various cable insulation materials. The distribution of degradation in film samples was investigated with various techniques. It was found that the antioxidant agent for stabilizer of insulation materials is closely related to the synergism. With progress of ageing, the concentration of effective antioxidant decreases by radiation decomposition and also by evaporation in thermal ageing. When the concentration of antioxidant is reduced to a limited value, the thermal oxidation is progressing.