Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Hasegawa, Kunio; Strnadel, B.*; Li, Y.; Lacroix, V.*
Journal of Pressure Vessel Technology, 144(6), p.061202_1 - 061202_6, 2022/12
Times Cited Count：0 Percentile：0(Engineering, Mechanical)When pipe walls are thin, part-through flaws are easily develop into through-wall flaws, and the likelihood of coolant leakage is high. The ASEM Code Section XI provides final allowable flaw angles of through-wall flaw for thin-wall pipes. The final allowable angles are applied to pipes in order to maintain structural integrity if the part-through flaws become through-wall flaws. To ensure that this stability is compromised, plastic collapse stresses for through-wall flaws are combined with allowable stresses. However, the final allowable angles of through-wall flaws are not identified for thin-walled pipes. This paper compares plastic collapse stresses of through-wall flaws and allowable stresses of part-through flaws for pipes. The comparison of these stresses is used to derive the final allowable angles of through-wall flaws. The angles can be expressed either in the form of exact solutions or as conventional options that are appropriate for various service level conditions.
Hasegawa, Kunio; Strnadel, B.*; Lacroix, V.*; Udyawar, A.*
International Journal of Pressure Vessels and Piping, 199, p.104722_1 - 104722_5, 2022/10
Times Cited Count：0 Percentile：0(Engineering, Multidisciplinary)Fully plastic collapse stresses for high toughness pipes with circumferential cracks subjected to tensile loading can be predicted by Limit Load Criteria. The Limit Load Criteria are provided by the ASME Code Section XI. Allowable membrane stresses for part-through cracks were determined by plastic collapse stresses in combination with safety factors. The allowable stresses decrease with increasing angles of the part-through cracks. When crack angles are large, the allowable stresses of the part-through cracks are larger than the collapse stresses of through-wall cracks. For such large cracks, allowable stresses greater than the collapse stresses cause instability, and are thus detrimental to pipe integrity, especially in thin-wall pipes. In order to avoid the anxiety, it is necessary to establish maximum allowable crack angles. This paper proposes maximum allowable crack angles for allowable stresses.
Lacroix, V.*; Hasegawa, Kunio; Li, Y.; Yamaguchi, Yoshihito
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 7 Pages, 2022/07
Yamaguchi, Yoshihito; Hasegawa, Kunio; Li, Y.; Lacroix, V.*
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 4 Pages, 2022/07
Lacroix, V.*; Dulieu, P.*; Hasegawa, Kunio; Mares, V.*
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 7 Pages, 2022/07
In the ASME Code Section XI, a simplified approach is proposed: a nonplanar flaw is resolved into two planar flaws by projection of the flaw area into planes normal to the maximum principal stress. However, simplified resolution of nonplanar flaws is not conservative for all types of loading and flaw inclinations. Consequently, an improvement of the resolutions of nonplanar flaws must be provided in the ASME Code Section XI. This paper carries out an exhaustive assessment of the conservatism of the ASME approach and then proposes an alternative approach to deal with nonplanar flaws allowing to overcome the non-suitability of current ASME Code.
Lacroix, V.*; Dulieu, P.*; Hasegawa, Kunio
Proceedings of ASME 2021 Pressure Vessels and Piping Conference (PVP 2021) (Internet), 5 Pages, 2021/07
When flaws are detected, assessments are done to demonstrate the fitness-for-service. The first step is the flaw characterization determining the flaw geometry for analyses. This key step is done by flaw characterization rules provided in FFS Codes. According to the flaw characterization rules of ASME Code Section XI, a nonplanar flaw shall be resolved into two planar flaws by projection of the flaw area into planes normal to the maximum principal stresses. This approach allows to simplify the flaw assessment but remains conservative. Therefore, the conservatisms by the simplified projection for nonplanar flaws are investigated in this paper. Current computations have been improved so that the modelling of nonplanar flaws are not significant difficulty. This paper compares the stress intensity factors (SIF) of projected nonplanar flaws and the mixed mode SIF of actual nonplanar flaws. The scope is to quantify how the flaw projection into planes normal to the maximum principal stresses is conservative.
Desclaux, C.*; Lacroix, V.*; Hasegawa, Kunio
Proceedings of ASME 2021 Pressure Vessels and Piping Conference (PVP 2021) (Internet), 10 Pages, 2021/07
The plastic collapse bending stress for a pipe is defined in ASME Code Section XI, using simplified equilibrium equations. One of the authors demonstrated that the simplified equilibrium equations are not conservative for externally cracked pipes and he proposed taking into account the cracked ligament mean radius. This paper demonstrates that the accuracy of the collapse bending stress equation can be refined considering the neutral axis position of the cracked pipe section. This leads to exact collapse bending moment equations. As the results, it is shown that the ASME equations for externally cracked pipes might be less conservative collapse bending stress than with the exact equations.
Hasegawa, Kunio; Li, Y.; Lacroix, V.*; Mare
, V.*
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 6 Pages, 2020/08
Authors have developed more precise equations using the Limit Load Criteria, which is called Modified Limit Load Criteria, hereafter. As the results of the Modified Limit Load Criteria, failure stresses for external flawed pipes are always smaller than the failure stresses obtained by the Limit Load Criteria provided by the ASME Code Section XI. It seems that the allowable flaw sizes of the Acceptance Standards provided by the ASME Code Section XI are less conservative for external flaws. The objective of this paper is to demonstrate difference of failure stresses by the Limit Load Criteria and Modified Limit Load Criteria for external flawed pipes. In addition, the allowable flaws of the Acceptance Standards are examined by large and small diameter pipes with external flaws using the Modified Limit Load Criteria.
Dulieu, P.*; Lacroix, V.*; Hasegawa, Kunio
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 7 Pages, 2020/08
When detected flaws are in close proximity, proximity rules given in the Fitness-foe Service codes require to combine the interacting flaws into a single flaw. ASME Code Case N877-1 provides alternative proximity rules for multiple radial oriented planar flaws. The calculations of flaw interaction have been performed under pure membrane stress. However, actual loading conditions induce non-uniform stresses in the component thickness direction. The objective of this paper is assess the suitability of ASME Code Case N877-1 with regards to the presence of a bending part in the applied stress distribution. For that purpose, various applied stress profiles and flaw configurations are covered. The effect on flaw interaction is assessed trough three-dimensional XFEM analyses.
Lacroix, V.*; Dulieu, P.*; Hasegawa, Kunio; Mare, V.*
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 8 Pages, 2020/08
When flaws are detected in pressure retaining components, a flaw characterization has to be carried out in order to determine unequivocally the flaw geometry. This flaw characterization is done according to rules provided in the FFS codes. The first step of the flaw characterization addresses the interaction of the flaw and the free surface. The second step of the flaw characterization addresses the interaction of the flaw with the adjacent flaws. In the ASME Code Sec. XI, there is a lack on how to treat the interaction of a combined flaw and the free surface of the component. The ASME Code Sec. XI flaw characterization is not clear. Some typical examples of unrealistic flaw assessment rules are depicted in this paper. The paper is used as technical basis for improvement of the ASME Code in order to clarify the treatment of combined flaw in the flaw characterization (IWA-3300, IWB/IWC-3510-1)
Hasegawa, Kunio; Li, Y.; Lacroix, V.*; Mare, V.*
Journal of Pressure Vessel Technology, 142(3), p.031506_1 - 031506_7, 2020/06
Times Cited Count：1 Percentile：11.94(Engineering, Mechanical)Bending stress at plastic collapse for a circumferentially cracked pipe is predicted by limit load criterion provided by the Appendix C of the ASME Code Section XI. The equation of the Appendix C is applicable for pipes with both external and internal surface cracks. On the other hand, the authors have developed a more precise equation. From the comparison of Appendix C equation and the new equation, the plastic collapse stress estimated by the Appendix C equation gives less conservative bending capacity prediction for external cracked pipes with thick wall thickness and large crack angle. This paper discusses the limitation scope to use the limit load criterion of the Appendix C equation.
Hasegawa, Kunio; Li, Y.; Lacroix, V.*; Mare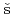, V.*
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 8 Pages, 2019/07
Bending stress at plastic collapse for a circumstantially cracked pipe is predicted by limit load equation provided by the Appendix C of the ASME Code Section XI. The equation of the Appendix C is applicable for pipes with both external and internal surface cracks. On the other hand, authors had developed an equation taking into account the pipe mean radii at non-cracked area and at cracked ligament area. From the comparison of Appendix C equation and the new equation, the plastic collapse stress estimated by the Appendix C equation gives 20 to 30% less conservative for external cracked pipes with small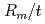 
, where 
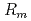is the pipe mean radius and t is the pipe wall thickness. This paper discusses the limitation of the use of 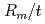for the Appendix C equation.
Hasegawa, Kunio; Usami, Saburo*; Lacroix, V.*
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 6 Pages, 2019/07
Fatigue crack growth thresholds are provided by several fitness-for-service (FFS) codes. When evaluating cracked components subjected to cyclic loading, maximum stress intensity factor and/or minimum stress intensity factor are required. However, the definitions of the thresholds under negative stress ratio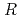 
are not clearly written. In addition, the thresholds are given by constant values under negative 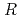. This paper shows that the maximum stress intensity factor converted by the thresholds obtained by experimental data are not constant values under negative 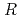. The thresholds for the FFS codes are less conservative. The definition of the thresholds under negative 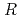ratio are discussed.
Bouydo, A.*; Dulieu, P.*; Lacroix, V.*; Hasegawa, Kunio; Mare, V.*
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 10 Pages, 2019/07
Dulieu, P.*; Lacroix, V.*; Hasegawa, Kunio
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 9 Pages, 2019/07
Hasegawa, Kunio; Li, Y.; Kim, Y.-J.*; Lacroix, V.*; Strnadel, B.*
Journal of Pressure Vessel Technology, 141(3), p.031201_1 - 031201_5, 2019/06
Times Cited Count：0 Percentile：0(Engineering, Mechanical)When discrete multiple flaws are in the same plane, and they are close to each other, it can be determined whether they are combined or standalone in accordance with combination rules provided by Fitness-For-Service (FFS) codes. However, specific criteria of the rules are different amongst these FFS codes. On the other hand, plastic collapse bending stresses for stainless steel pipes with two circumferential similar flaws were obtained by experiments and the prediction procedure for collapse stresses for pipes with two similar flaws were developed analytically. Using the experimental data and the analytical procedure, plastic collapse stresses for pipes with two similar flaws are compared with the stresses in compliance with the flaw combination criteria. It is shown that the calculated plastic collapse stresses based on the flaw combination criteria are significantly different from the experimental and analytical stresses.
Mare, V.*; Hasegawa, Kunio; Li, Y.; Lacroix, V.*
Journal of Pressure Vessel Technology, 141(2), p.021203_1 - 021203_6, 2019/04
Times Cited Count：4 Percentile：31.03(Engineering, Mechanical)Appendix C-5320 of ASME BPV Code Section XI provides an equation of bending stress at the plastic collapse, where the equation is applicable for both inner and outer surface cracks. That is, the collapse stresses for pipes with inner and outer surface cracks are the same. Authors considered the separated pipe mean radii at the cracked ligament and at the un-cracked ligament and equations of plastic collapse stresses for both inner and outer cracked pipes were developed. As the results of the calculations, when the crack angle and depth are the same, the collapse stress for outer cracked pipe is lower than that calculated by the Appendix C equation. It is found that the Appendix C equation gives un-conservative plastic collapse stress.
Hasegawa, Kunio*; Strnadel, B.*; Li, Y.; Lacroix, V.*
Journal of Pressure Vessel Technology, 140(5), p.051204_1 - 051204_7, 2018/10
Times Cited Count：0 Percentile：0(Engineering, Mechanical)Hasegawa, Kunio; Li, Y.; Mare, V.*; Lacroix, V.*
Proceedings of 2018 ASME Pressure Vessels and Piping Conference (PVP 2018), 5 Pages, 2018/07
Appendix C-5320 of ASME Code Section XI provides a formula of bending stress at the plastic collapse, where the formula is applicable for both inner and outer surface flaws. Authors considered the separated pipe mean radii at the flawed ligament and at the un-flawed ligament and formulas of plastic collapse stresses for each inner and outer flawed pipe were obtained. It is found that the collapse stress for inner flawed pipe is slightly higher than that calculated by Appendix C-5320 formula, and the collapse stress for outer flawed pipe is slightly lower than that by Appendix C-5320 formula. The collapse stresses derived from the three formulas are almost the same in most instances. For less common case where the flaw angle and depth are very large for thick wall pipes, the differences among the three collapse stresses become large.
Hasegawa, Kunio; Li, Y.; Kim, Y.-J.*; Lacroix, V.*; Bohumir, S.*
Proceedings of 2018 ASME Pressure Vessels and Piping Conference (PVP 2018), 6 Pages, 2018/07
When discrete multiple flaws are close to each other, it is determined whether they are combined or standalone in accordance with combination rules provided by fitness-for-service codes. However, specific criteria of the rules are different. On the other hand, plastic collapse bending stresses for stainless steel pipes with circumferential twin flaws were obtained by experiments. Using the experimental data and the analytical procedure, plastic collapse stresses for pipes with twin flaws are compared with the stresses in compliance with the combination criteria. It is shown that the calculated plastic collapse stresses based on the combination criteria are significantly different from the experimental and analytical stresses.
