Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
荒木 康史; 三澤 貴宏*; 野村 健太郎*
Physical Review Research (Internet), 3(2), p.023219_1 - 023219_15, 2021/06
本論文では、トポロジカルディラック半金属(TDSM)表面のギャップレス状態を介した、長距離スピン伝送を理論面から提案する。次世代のスピントロニクス素子の構築のためには、散逸の少ないスピン流を実現することが必要である。主要なスピン流のキャリアは金属中の伝導電子や磁性絶縁体中のスピン波であるが、これらはジュール熱やギルバート緩和により伝播距離が制限される問題がある。本研究ではTDSM(Cd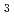 As
As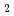 , Na
, Na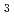 Bi等)のスピン・ヘリカルな表面状態が、乱れに対して頑強である性質を用いて、低散逸で長距離のスピン輸送を提案する。2つの磁性絶縁体とTDSMの接合系を考え、一方の磁性体の磁化ダイナミクスにより、TDSM表面を介して他方の磁性体に注入されるスピン流に注目する。表面における輸送理論と、格子模型による実時間発展シミュレーションを併用することにより、TDSM表面を流れるスピン流は準量子化された値をとり、その値は界面の微視的な結合の構造によらないことを示す。さらに、このスピン流は長距離においても乱れに対して強いことを示し、TDSMがスピントロニクス素子へ応用可能な表面状態をもつことを提案する。
Bi等)のスピン・ヘリカルな表面状態が、乱れに対して頑強である性質を用いて、低散逸で長距離のスピン輸送を提案する。2つの磁性絶縁体とTDSMの接合系を考え、一方の磁性体の磁化ダイナミクスにより、TDSM表面を介して他方の磁性体に注入されるスピン流に注目する。表面における輸送理論と、格子模型による実時間発展シミュレーションを併用することにより、TDSM表面を流れるスピン流は準量子化された値をとり、その値は界面の微視的な結合の構造によらないことを示す。さらに、このスピン流は長距離においても乱れに対して強いことを示し、TDSMがスピントロニクス素子へ応用可能な表面状態をもつことを提案する。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
Physical Review Research (Internet), 2(2), p.023195_1 - 023195_11, 2020/05
We theoretically manifest that the edge of a quantum spin Hall insulator (QSHI), attached to an insulating ferromagnet (FM), can realize a highly efficient spin-to-charge conversion. Based on a one-dimensional QSHI-FM junction, the electron dynamics on the QSHI edge is analyzed, driven by a magnetization dynamics in the FM. Under a large gap opening on the edge from the magnetic exchange coupling, we find that the spin injection into the QSHI edge gets suppressed while the charge current driven on the edge gets maximized, demanded by the band topology of the one-dimensional helical edge states.
八木 貴宏*; 三澤 毅*; Pyeon, C. H.*; 宇根崎 博信*; 代谷 誠治*; 川口 真一*; 岡嶋 成晃; 谷 和洋*
Proceedings of International Conference on the Physics of Reactors, Nuclear Power; A Sustainable Resource (PHYSOR 2008) (CD-ROM), 8 Pages, 2008/09
燃料板のギャップのような狭い空隙に中性子検出器を挿入して、リアル・タイムで高速中性子を測定するために、光ファイバーを用いた中性子検出器が開発されてきた。この検知器は、先端が中性子を検出する物質とZnS(Ag)のようなシンチレーターの混合体で覆われた光ファイバーから成る。高速中性子用の光ファイバー検出器には、中性子を検出する物質として、これまで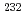 Thが利用されてきた。これは、
Thが利用されてきた。これは、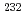 Thが高速中性子と核分裂反応を起こすことを利用している。しかし、
Thが高速中性子と核分裂反応を起こすことを利用している。しかし、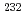 Thが核燃料物質であることから、その使用場所が限定されてしまう。そこで、本研究では、
Thが核燃料物質であることから、その使用場所が限定されてしまう。そこで、本研究では、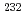 Thを利用しないで高速中性子を測定することができる新たな光ファイバー検出器を開発し、その検知器特性を調べた。検出器特性を調べるために、D-T中性子発生装置のターゲット近傍の高速中性子束分布及び高速炉臨界実験装置における高速中性子束分布測定を行い、放射化法による結果と比較した。その結果、ZnS(Ag)を用いた新たな光ファイバー検知器による高速中性子束分布測定結果は放射化法で測定した結果と一致し、ZnS(Ag)を用いた光ファイバー検知器が高速中性子測定に有効であることがわかった。
Thを利用しないで高速中性子を測定することができる新たな光ファイバー検出器を開発し、その検知器特性を調べた。検出器特性を調べるために、D-T中性子発生装置のターゲット近傍の高速中性子束分布及び高速炉臨界実験装置における高速中性子束分布測定を行い、放射化法による結果と比較した。その結果、ZnS(Ag)を用いた新たな光ファイバー検知器による高速中性子束分布測定結果は放射化法で測定した結果と一致し、ZnS(Ag)を用いた光ファイバー検知器が高速中性子測定に有効であることがわかった。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on spin pumping into a two-dimensional (2D) quantum spin Hall inslator (QSHI). Recent theories and experiments have demonstrated the QSHI phase in a monolayer of transition metal dichalcogenide 1T'-WTe2, which can be easily engineered in contrast to traditionally-known HgTe/CdTe and InAs/GaSb quantum wells. While the theory of spin pumping is well established in normal metals by focusing on the spin-dependent electron scattering at the interface, it is unreliable for topologically nontrivial interfaces in such systems. In the present work, we consider a junction of a ferromagnet and a 2D QSHI at its 1D edge, and demonstrate the pumping of angular momentum from the spin-precessing ferromagnet into the QSHI. Using the Floquet theory for the electrons on the helical edge states, we analytically show that the time-periodic precession of the magnetization drives a charge current on the edge, for the whole range of precession frequency. This edge current can be regarded as a consequence of the inverse spin Hall effect intrinsic to the QSHI, which converts the injected spin current into a transverse charge current. By varying the precession frequency of the magnetization and the coupling strength at the junction, we find a clear crossover between two regimes: the adiabatic regime, where the slow magnetization precession drives a quantized pumping, and the resonant regime, where the fast precession leads to a suppressed pumping. We also incorporate the effect of orbital dependence in the exchange coupling at the edge, and show numerically that it shifts the crossover point between the adiabatic and resonant regimes.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
Cd As
As 等のトポロジカルディラック半金属の表面には、フェルミアークとしてスピンヘリカルな1次元的状態が存在する。本講演ではこの表面状態を介したスピン輸送について議論する。半金属表面に2つの磁性絶縁体が接合した状況を考え、片方の磁性体の磁化ダイナミクスが、半金属表面状態を介して他方の磁性体に与えるスピン流を扱う。このスピン流がフェルミアークの長さに応じた量子化値をとることを、解析的および数値的に示す。
等のトポロジカルディラック半金属の表面には、フェルミアークとしてスピンヘリカルな1次元的状態が存在する。本講演ではこの表面状態を介したスピン輸送について議論する。半金属表面に2つの磁性絶縁体が接合した状況を考え、片方の磁性体の磁化ダイナミクスが、半金属表面状態を介して他方の磁性体に与えるスピン流を扱う。このスピン流がフェルミアークの長さに応じた量子化値をとることを、解析的および数値的に示す。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on dynamical spin-to-charge conversion at the edge of a quantum spin Hall insulator (QSHI), namely a two-dimensional topological insulator with helical edge states. Interconversion between spin- and charge-related quantities has been a key idea in making use of magnetic materials, especially in the context of spintronics. QSHI is a typical system showing a universal charge-to-spin conversion behavior, namely the quantum spin Hall effect, whereas the spin-to-charge conversion therein is still not clearly understood. At a lateral heterojunction of a ferromagnet (FM) and a QSHI, it has been theoretically demonstrated that magnetization dynamics induces a charge current along the edge of QSHI; however, its mechanism from the viewpoint of spin-to-charge conversion still remains to be clarified. In order to understand the spin transfer and the spin-to-charge conversion mechanism in QSHI, we investigate the many-body dynamics of the electrons under the magnetization dynamics at the QSHI-FM junction. We analytically treat the electron dynamics in terms of the Floquet-Keldysh formalism, and compare two physical quantities present on the edge: the spin injection rate from the FM into the QSHI, and the charge current induced along the edge. Whereas the edge current seen in the previous works is reproduced, we find that it is not proportional to the spin injection rate, especially when the exchange interaction at the junction is strong enough. This relation implies that the spin-to-charge conversion in this system cannot be considered as the inverse spin Hall effect, while it can be rather seen as the inverse Edelstein effect, in which an electron spin accumulation at the junction is converted to a charge current. We also focus on the energy transfer at the junction, and interpret this phenomenon in terms of magnon exchange.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
The two-dimensional quantum spin Hall insulator (2D QSHI) is the most primitive but quite important realization of topological insulator. It shows the helical edge states protected by time-reversal symmetry, whereas the quantized spin Hall conductivity in the bulk. In the present work, we theoretically investigate the spin pumping from a precessing ferromagnet into a 2D QSHI thoroughly from the adiabatic to nonadiabatic regimes, both analytically and numerically. We analytically treat the dynamics of the edge-state electrons coupled to the precessing ferromagnet by the Floquet theory, and derive the pumped current as a function of the exchange energy and the precession frequency. We find that a heat bath for the edge electrons governs the transition between the adiabatic and nonadiabatic regime: when the edge electrons are coupled with a heat bath, their spin and energy can dissipate into the bath by a certain rate, eventually reaching a periodic steady state. The pumped current on the becomes quantized when the exchange energy exceeds the dissipation rate. We also calculate the edge current numerically on the 2D lattice model, and find that the bulk states in the QSHI effectively serves as the heat bath for the edge electrons.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on spin pumping into a two-dimensional (2D) quantum spin Hall inslator (QSHI). QSHI is a topological insulator in 2D exhibiting gapless helical edge stats, which are responsible for the quantized spin Hall conductivity. Recent theories and experiments have demonstrated the QSHI phase in a monolayer of transition metal dichalcogenide 1T'-WTe2, which can be easily engineered in contrast to traditionally-known HgTe/CdTe and InAs/GaSb quantum wells. While the theory of spin pumping is well established in normal metals by focusing on the spin-dependent electron scattering at the interface, it is unreliable for topologically nontrivial interfaces in such systems. In the present work, we consider a junction of a ferromagnet and a 2D QSHI at its 1D edge, and demonstrate the pumping of angular momentum from the spin-precessing ferromagnet into the QSHI. Using the Floquet theory for the electrons on the helical edge states, we analytically show that the time-periodic precession of the magnetization drives a charge current on the edge, for the whole range of precession frequency. This edge current can be regarded as a consequence of the inverse spin Hall effect intrinsic to the QSHI, which converts the injected spin current into a transverse charge current. By varying the precession frequency of the magnetization and the coupling strength at the junction, we find a clear crossover between two regimes: the adiabatic regime, where the slow magnetization precession drives a quantized pumping, and the resonant regime, where the fast precession leads to a suppressed pumping. We also incorporate the effect of orbital dependence in the exchange coupling at the edge, and show numerically that it shifts the crossover point between the adiabatic and resonant regimes.