Advance in integrated modelling towards prediction and control of JT-60SA plasmas

Hayashi, Nobuhiko; Honda, Mitsuru; Shiraishi, Junya; Miyata, Yoshiaki; Wakatsuki, Takuma; Hoshino, Kazuo; Toma, Mitsunori; Suzuki, Takahiro; Urano, Hajime; Shimizu, Katsuhiro; et al.

Europhysics Conference Abstracts (Internet), 39E, p.P5.145_1 - P5.145_4, 2015/06

http://ocs.ciemat.es/EPS2015PAP/pdf/P5.145.pdf

Simulation of plasma current ramp-up with reduced magnetic flux consumption in JT-60SA

Wakatsuki, Takuma; Suzuki, Takahiro; Hayashi, Nobuhiko; Shiraishi, Junya; Ide, Shunsuke; Takase, Yuichi*

Plasma Physics and Controlled Fusion, 57(6), p.065005_1 - 065005_12, 2015/06

https://doi.org/10.1088/0741-3335/57/6/065005

MHD instability excited by interplay between resistive wall mode and stable MHD modes in rotating tokamak plasmas

Aiba, Nobuyuki; Hirota, Makoto*; Matsuyama, Akinobu; Shiraishi, Junya; Bierwage, A.

Proceedings of 25th IAEA Fusion Energy Conference (FEC 2014) (CD-ROM), 8 Pages, 2014/10

A mechanism exciting magnetohydrodynamic (MHD) instabilities in rotating tokamak plasmas is found numerically for the first time. This mechanism is the interplay between a resistive wall mode (RWM) and a stable MHD mode. When the plasma has a stable discrete eigenmode, a reversed shear Alfv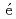n eigenmode (RSAE) for example, a MHD mode is destabilized when plasma equilibrium rotation frequency is similar to the frequency of this stable eigenmode in a static equilibrium. This destabilization is also observed even when the eigenmode couples with Alfv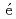n continua. This result suggests that for steady state high beta tokamaks, like DEMO, it is necessary to shape the safety factor profile in such a way that no stable eigenmode exists in the band of rotation frequency.

On kinetic resistive wall mode theory with sheared rotation

Shiraishi, Junya; Miyato, Naoaki; Matsunaga, Go

Plasma and Fusion Research (Internet), 9, p.3403027_1 - 3403027_4, 2014/04

https://doi.org/10.1585/pfr.9.3403027

To investigate the rotation shear effect on the RWM (Resistive Wall Mode) stability, we generalize the formalism of kinetic RWM theory to include a general equilibrium rotation. Starting from the guiding-center Lagrangian with the non-uniform rotation, we generalize the energy functional associated with the drift-kinetic resonance. By the generalized kinetic energy functional, we derive a new dispersion relation in the large aspect ratio limit. Numerical analysis of the new dispersion relation indicates that the rotation shear stabilizes the RWMs as observed in experiments

Stabilization of resistive wall modes by magnetohydrodynamic equilibrium change induced by plasma toroidal rotation

Shiraishi, Junya; Aiba, Nobuyuki; Miyato, Naoaki; Yagi, Masatoshi

Proceedings of 24th IAEA Fusion Energy Conference (FEC 2012) (CD-ROM), 8 Pages, 2013/03

http://www-naweb.iaea.org/napc/physics/FEC/FEC2012/papers/314_THP319.pdf

Effects of plasma toroidal rotation are self-consistently taken into account not only in the magnetohydrodynamic (MHD) stability analysis but also in the equilibrium calculation. To study the effects of toroidal rotation on resistive wall modes (RWMs), a new code has been developed. The RWMaC modules, which solve the electromagnetic dynamics in vacuum and the resistive wall, have been implemented in the MINERVA code, which solves the Frieman-Rotenberg equation that describes the linear ideal MHD in a rotating plasma. It is shown for the first time that MHD equilibrium change induced by toroidal rotation significantly reduces the growth rates of RWMs. Moreover, it can open the stable window which does not exist under the assumption that the rotation affects only the linear dynamics. The rotation modifies the equilibrium pressure, current density, and mass density profiles, which results in the change of the potential energy including rotational effects.

Impact of plasma rotation on the linear physics of resistive wall modes in tokamaks

Aiba, Nobuyuki; Shiraishi, Junya; Hirota, Makoto

Plasma Physics and Controlled Fusion, 55(7), p.074002_1 - 074002_7, 2013/00

https://doi.org/10.1088/0741-3335/55/7/074002

The authors identified that plasma poloidal rotation sometimes plays an important role for ideal MHD stability due to changing the Doppler-shift frequency. As the result, the stability of edge localized MHD mode can depends on the direction of toroidal rotation; this dependence is qualitatively consistent with the experimental results observed in JT-60U. Plasma rotation is also responsible for the stability of resistive wall mode (RWM). In reversed shear plasmas, plasma rotation once stabilize this RWM but destabilize this again when rotation frequency reaches to certain frequency. This re-destabilization is thought to be related to the coupling between RWM and a stable MHD wave; this coupling is one of the destabilizing mechanisms discussed in previous theoretical papers. This re-destabilized RWM can become unstable in the plasma whose beta value is below no-wall beta limit.

Analytic dispersion relation for resistive wall modes in rotating plasmas by generalized matching theory

Shiraishi, Junya; Tokuda, Shinji*

Nuclear Fusion, 51(5), p.053006_1 - 053006_9, 2011/05

https://doi.org/10.1088/0029-5515/51/5/053006

Analytic dispersion relation is derived for resistive wall modes (RWMs) in rotating plasmas, which gives the growth rate and the real frequency. The given parameters are wall information (radius, thickness, and volume resistivity) and equilibrium quantities at a plasma surface and near the singular point of the generalized Newcomb equation, which is an inertia-less linearized ideal magnetohydrodynamic equations with equilibrium rotation. Derivation of the dispersion relation is based on the generalized matching theory proposed by present authors, which exploits the inner "region" with finite width. It is found that the RWM stability is strongly affected by the rotation shear at the singular point of the generalized Newcomb equation, not at the rational surface.

Impact of plasma poloidal rotation on resistive wall mode instability in toroidally rotating plasmas

Aiba, Nobuyuki; Shiraishi, Junya; Tokuda, Shinji*

Physics of Plasmas, 18(2), p.022503_1 - 022503_5, 2011/02

https://doi.org/10.1063/1.3551731

Rotation effect on the stability of the resistive wall mode (RWM) is investigated in a cylindrical plasma and a toroidal plasma with not only a toroidal rotation but also a poloidal rotation. In the case that a poloidal rotation frequency is not so large, the effect of a poloidal rotation can be treated with the modified toroidal rotation frequency, which is determined by subtracting a toroidal component of the rotation parallel to the magnetic field from the toroidal rotation frequency. This effect of a poloidal rotation on the RWM stability depends on its rotational direction, and when this modified toroidal rotation frequency is larger than the original toroidal rotation frequency, a poloidal rotation enhances the stabilizing effect of a rotation on RWM stability. This result indicates that a poloidal rotation produces a dependence of the critical toroidal rotation frequency for stabilizing RWM on the rotational direction of a toroidal rotation in the same magnetic configuration.

A Matching problem revisited for stability analysis of resistive wall modes in flowing plasmas

Shiraishi, Junya; Tokuda, Shinji; Aiba, Nobuyuki

Physics of Plasmas, 17(1), p.012504_1 - 012504_9, 2010/01

https://doi.org/10.1063/1.3286435

The classical matching problem for magnetohydrodynamic stability analysis is revisited to study effects of the plasma flow on the resistive wall modes (RWMs). The Newcomb equation, which describes the marginal states and governs the regions except for the resonant surface, is generalized to analyze the stability of flowing plasmas. When there exists no flow, the singular point of the Newcomb equation and the resonant surface degenerate into the rational surface. The location of the rational surface is prescribed by the equilibrium, hence the inner layer, which must contain the resonant surface, can be set a priori. When the flow exists, the singular point of the Newcomb equation splits in two due to the Doppler shift. Additionally, the resonant surface deviates from the singular points and the rational surface if the resonant eigenmode has a real frequency. Since the location of the resonant surface depends on the unknown real frequency, it can be determined only a posteriori. Hence the classical asymptotic matching method cannot be applied. This paper shows that a new matching method that generalizes the asymptotic one to use the inner layer with finite width works well for the stability analysis of flowing plasmas. If the real frequency is limited in a certain range such as the RWM case, the resonance occurs somewhere in the finite region around the singular points, hence the inner layer with finite width can capture the resonant surface.

Topological transition from accretion to ejection in a disk-jet system; Singular perturbation of the Hall effect in a weakly ionized plasma

Shiraishi, Junya; Yoshida, Zensho*; Furukawa, Masaru*

Astrophysical Journal, 697(1), p.100 - 105, 2009/03

https://doi.org/10.1088/0004-637X/697/1/100

A thin disk accompanied by spindle-like jet, created commonly near massive central objects, exhibits a topologically singular aspect when viewed from an ideal macroscopic theory. The accreting inflow and jet's outflow are "singular perturbation" on the ambient Keplerian rotation, which are generated by some non-ideal higher-order (in the order of derivatives) effect. The Hall effect can generate such a structure in a weakly ionized plasma of a protostellar disk. Numerical estimate of the characteristic length scale defined by the singular perturbation justifies the precedence of the Hall effect.