Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
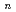 (
(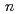 =1-4) by all-electron Dirac-Hartree-Fock calculations
=1-4) by all-electron Dirac-Hartree-Fock calculations望月 祐志*; 舘脇 洋*
Journal of Chemical Physics, 118(20), p.9201 - 9207, 2003/05
被引用回数:6 パーセンタイル:18.14(Chemistry, Physical)弗化物はアクチニドのポピュラーな化合物であるが、原子力エネルギー分野の主役であるUとPuの弗化物を例外として他の元素についてはほとんど知見が得られていない。しかし、ランタニドと比較すると後期のアクチニドでも+4価と取れるなど化学的な差異は知られており、計算によってこうした側面に切り込むことが出来れば、原子力工学・基礎無機化学にとって大きな意味が期待される。本研究では、CmとGdを例に取って、4弗化物までをDirac-Hartree-Fock計算によって系統的に調べた。本結果から、「CmF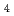 が合成可能なのに、GdF
が合成可能なのに、GdF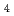 が不可能な理由」,中心金属の実効電子配置などの知見が世界で初めて明らかにされた。大規模並列計算としても、当該分野で過去最大のものである。
が不可能な理由」,中心金属の実効電子配置などの知見が世界で初めて明らかにされた。大規模並列計算としても、当該分野で過去最大のものである。
舘脇 洋*; 望月 祐志*
Theoretical Chemistry Accounts, 109(1), p.40 - 42, 2003/01
被引用回数:23 パーセンタイル:52.43(Chemistry, Physical)Dirac-Hartree-Fockを始め、4成分の相対論的分子軌道計算を行うにあたって、変分崩壊を起こしにくく、またいわゆる「基底関数重ね合わせ誤差」の少ない基底関数の選択は重要である。しかし、4成分計算は計算コストが高いために、非対称論系の基底に比して選択すべき候補も少なく、また検証も未だ進んでいない。本論文ではこうした状況をふまえ、キュリウムとその弗化物を例に取り、基底関数選択にあたっての注意点を考察し、簡潔にまとめた。
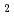 O)
O)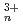 (n=1, 2, 4, 6) by all-electron Dirak-Hartree-Fock calculations
(n=1, 2, 4, 6) by all-electron Dirak-Hartree-Fock calculations望月 祐志*; 舘脇 洋*
Journal of Chemical Physics, 116(20), p.8838 - 8842, 2002/05
被引用回数:16 パーセンタイル:45.25(Chemistry, Physical)全電子のDirac-Hartree-Fock法を並列処理を駆使することによって、3価キュリウムイオンの6水和錯体モデルにまで適用した。さらに、蛍光スペクトルの評価のために閉殻完全CI計算も行った。同様の計算を等電子系のガドリニウムイオンについても用い、結果をキュリウムの場合と比較した。一連の計算により、水和の本質が配位結合による安定化であること、水側からイオンへ相当量の電子供与があること、結果として蛍光スペクトルが赤方レフトすること等が明らかになった。
望月 祐志*; 舘脇 洋*
Chemical Physics, 273(2-3), p.135 - 148, 2001/11
被引用回数:23 パーセンタイル:58.82(Chemistry, Physical)4成分の相対論的分子軌道計算(Dirac-Hartree-Fock,Relativistic M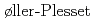 摂動)により、3価のランタノイド,アクチノイドイオンと水分子との錯体を系統的に調べ、イオン-水分子間距離,安定化エネルギーMulliken密度などを評価した。本計算から、相対論効果の大きさ、並びに相対論と電子相関の分離性が示されたほか、錯体における電子的相互作用の描像が明らかになった。
摂動)により、3価のランタノイド,アクチノイドイオンと水分子との錯体を系統的に調べ、イオン-水分子間距離,安定化エネルギーMulliken密度などを評価した。本計算から、相対論効果の大きさ、並びに相対論と電子相関の分離性が示されたほか、錯体における電子的相互作用の描像が明らかになった。