Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Oyama, Naoyuki; Kojima, Atsushi; Tokuda, Shinji*; Yagi, Masatoshi
Nuclear Fusion, 51(7), p.073012_1 - 073012_9, 2011/07
Times Cited Count：21 Percentile：65.54(Physics, Fluids & Plasmas)Mechanisms of plasma rotation on edge MHD stability is investigated numerically by introducing energies that are distinguished by physics. By comparing them, it is found that an edge localized MHD mode is destabilized by the difference between an eigenmode frequency and an equilibrium toroidal rotation frequency, which is induced by rotation shear. In addition, this destabilizing effect becomes effective in the shorter wavelength region. The effect of poloidal rotation on the edge MHD stability is also investigated. Under the assumption that the change of an equilibrium by poloidal rotation is negligible, it is identified numerically that poloidal rotation can have both the stabilizing effect and the destabilizing effect on the edge MHD stability, which depends on the direction of poloidal rotation. Numerical analysis demonstrates that these effects of plasma rotation in both toroidal and poloidal directions can play important roles on type-I ELM phenomena in JT-60U H-mode plasmas.
Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Oyama, Naoyuki; Kojima, Atsushi; Tokuda, Shinji*; Yagi, Masatoshi
Nuclear Fusion, 51(7), p.073012_1 - 073012_9, 2011/07
We investigate numerically the destabilizing effect of a toroidal rotation on the edge localized MHD mode, which induces the large amplitude edge localized mode (ELM). As the results of this analysis, we reveal that the toroidal rotation with shear can destabilize this MHD mode, and the destabilization is caused by the difference between the plasma rotation frequency and the frequency of the unstable mode. Based on these results, we investigate numerically the stability of JT-60U type-I ELMy H-mode plasmas, and show that the toroidal rotation plays an important role for making the difference of ELM behavior observed in JT-60U plasmas with different plasma rotation profiles.
Shiraishi, Junya; Tokuda, Shinji*
Nuclear Fusion, 51(5), p.053006_1 - 053006_9, 2011/05
Times Cited Count：4 Percentile：19.28(Physics, Fluids & Plasmas)Analytic dispersion relation is derived for resistive wall modes (RWMs) in rotating plasmas, which gives the growth rate and the real frequency. The given parameters are wall information (radius, thickness, and volume resistivity) and equilibrium quantities at a plasma surface and near the singular point of the generalized Newcomb equation, which is an inertia-less linearized ideal magnetohydrodynamic equations with equilibrium rotation. Derivation of the dispersion relation is based on the generalized matching theory proposed by present authors, which exploits the inner "region" with finite width. It is found that the RWM stability is strongly affected by the rotation shear at the singular point of the generalized Newcomb equation, not at the rational surface.
Shiraishi, Junya; Tokuda, Shinji*
Proceedings of 23rd IAEA Fusion Energy Conference (FEC 2010) (CD-ROM), 8 Pages, 2011/03
no abstracts in English
B flow on gyrokineticsMiyato, Naoaki; Scott, B. D.*; Tokuda, Shinji*; Yagi, Masatoshi
Proceedings of 23rd IAEA Fusion Energy Conference (FEC 2010) (CD-ROM), 8 Pages, 2011/03
Based on the phase space Lagrangian Lie-transform perturbation method and the field theory, a reduced kinetic model with large E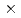B flow beyond the standard ordering (
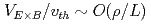) is constructed by modifying the guiding-centre phase space trans-formation. The model can be regarded as a natural extension of the standard model without flow since the symplectic part of the Lagrangian is the same as the standard one formally. Some aspects of the model are revealed and effects of the flow are discussed in course of comparison with the standard model. The push-forward representation of general particle fluid moment is presented in the subsonic flow case. In sonic flow case, corrections to the reduced quasi-neutrality condition due to the E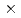B flow are found by variational derivation of the push-forward representation of particle density.
Aiba, Nobuyuki; Shiraishi, Junya; Tokuda, Shinji*
Physics of Plasmas, 18(2), p.022503_1 - 022503_5, 2011/02
Times Cited Count：13 Percentile：49.10(Physics, Fluids & Plasmas)Rotation effect on the stability of the resistive wall mode (RWM) is investigated in a cylindrical plasma and a toroidal plasma with not only a toroidal rotation but also a poloidal rotation. In the case that a poloidal rotation frequency is not so large, the effect of a poloidal rotation can be treated with the modified toroidal rotation frequency, which is determined by subtracting a toroidal component of the rotation parallel to the magnetic field from the toroidal rotation frequency. This effect of a poloidal rotation on the RWM stability depends on its rotational direction, and when this modified toroidal rotation frequency is larger than the original toroidal rotation frequency, a poloidal rotation enhances the stabilizing effect of a rotation on RWM stability. This result indicates that a poloidal rotation produces a dependence of the critical toroidal rotation frequency for stabilizing RWM on the rotational direction of a toroidal rotation in the same magnetic configuration.
Shiraishi, Junya; Tokuda, Shinji*
IEEE Transactions on Plasma Science, 38(9), p.2169 - 2176, 2010/09
Times Cited Count：1 Percentile：4.00(Physics, Fluids & Plasmas)Numerical implementation and a numerical property of a new matching scheme for stability analysis of flowing plasmas are presented. In the new scheme, the singularities are contained in the inner layer, and the Newcomb equation in the outer regions becomes regular, hence the new scheme is numerically tractable. Also, since the new scheme is based on the boundary layer theory, it can save much computation time.
Miyato, Naoaki; Scott, B. D.*; Tokuda, Shinji*
Journal of Plasma and Fusion Research SERIES, Vol.9, p.546 - 551, 2010/08
Generally guiding-centre (GC) or gyro-centre fluid moments are different from corresponding particle fluid moments due to finite Larmor radius effects. Recently we derived a modified GC fundamental 1-form with strong E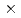B flow from which a GC Vlasov-Poisson system was also constructed through the field theory. In contrast to conventional formulations with strong E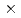B flow, the symplectic part of our GC 1-form is the same as that in the standard gyrokinetic model formally. The GC Hamiltonian also agrees with the standard gyrokinetic Hamiltonian in the long wavelength limit. Therefore it is expected that the relation between the fluid moments in the modified GC coordinates and the particle-fluid moments is similar to the one obtained from the standard gyrokinetic model in the long wavelength limit. We represent the particle fluid moment in terms of the modified GC fluid moments. The representation is compared with the standard gyrokinetic result.
Aiba, Nobuyuki; Oyama, Naoyuki; Kojima, Atsushi; Tokuda, Shinji*
Journal of Plasma and Fusion Research SERIES, Vol.9, p.74 - 78, 2010/08
Effect of the toroidal rotation on the type-I edge localized mode in JT-60U is investigated numerically. As the result of the numerical analysis, it is confirmed that the plasma rotating experimentally in the co-direction to the plasma current is approximately on the stability boundary of the MHD mode even when the rotation is neglected. However, the plasma rotating in the counter-direction is far from the stability boundary under the static assumption. Since both plasmas have the type-I ELM, the edge MHD stability is reassessed with the toroidal rotation effect. This stability analysis clarifies that the rotation of this counter rotating plasma can destabilize the edge localized MHD mode, and can explain the difference of the equilibrium profiles just before the ELM and between the co-rotating and the counter-rotating plasmas.
Hirota, Makoto; Tokuda, Shinji*
Physics of Plasmas, 17(8), p.082109_1 - 082109_11, 2010/08
Times Cited Count：8 Percentile：30.63(Physics, Fluids & Plasmas)Invariance of wave action for eigenmodes and continuum modes around quasi-stationary equilibrium state is investigated in a general framework that allows for the ideal magnetohydrodynamic system and the Vlasov-Maxwell system. By utilizing the averaging method for the variational principle, the wave action of each mode is shown to be conserved if its frequency (spectrum) is sufficiently separated from other ones, whereas some conservative exchange of the wave action may occur among the modes with close frequencies. This general conservation law is, as an example, demonstrated for a situation where the Landau damping (or growth) occurs due to a resonance between an eigenmode and a continuum mode. The damping (or growth) rate is closely related to the spectral linewidth (= the phase mixing rate) of the continuum mode, which can be estimated by the invariance of wave action without invoking the conventional analytic continuation of the dispersion relation.
Furukawa, Masaru*; Tokuda, Shinji; Zheng, L. J.*
Physics of Plasmas, 17(5), p.052502_1 - 052502_15, 2010/05
Times Cited Count：6 Percentile：23.40(Physics, Fluids & Plasmas)Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Tokuda, Shinji
Nuclear Fusion, 50(4), p.045002_1 - 045002_13, 2010/04
Times Cited Count：22 Percentile：63.87(Physics, Fluids & Plasmas)In this paper, we investigate numerically the destabilizing effect of a toroidal rotation on the edge localized MHD mode, which induces the large amplitude edge localized mode (ELM). As the results of this analysis, we reveal that the toroidal rotation with shear can destabilize this MHD mode, and the destabilization is caused by the difference between the plasma rotation frequency and the frequency of the unstable mode, which mainly affects the pressure-driven component of the unstable mode. This destabilizing effect becomes more effective as the wave length of the mode becomes shorter, but such a MHD mode with short wave length is also stabilized by the sheared toroidal rotation due to the Doppler-shift at each flux surfaces. We clarify that the stability of the edge localized MHD mode, whose wave length is typically intermediate, is determined by the balance between these stabilizing and destabilizing effects.
Kushida, Noriyuki; Takemiya, Hiroshi; Tokuda, Shinji*
Proceedings of 18th Euromicro International Conference on Parallel, Distributed and Network-Based Computing (PDP 2010), p.482 - 488, 2010/02
In this study, we developed a high speed eigenvalue solver that is the necessity of plasma stability analysis system for International Thermo-nuclear Experimental Reactor (ITER) on Cell cluster system. According to our estimation, the most time consuming part of analysis system is eigensolver. However, current supercomputer is not applicable for such instantaneous calculation, because the overhead of network communication becomes dominant. Therefore, we employ Cell cluster system, whose processor has higher performance than current supercomputer, because we can obtain sufficient processing power with small number of processors. Furthermore, we developed novel eigenvalue solver with the consideration of hierarchical architecture of Cell cluster Finally, we succeeded to solve the block tridiagonal Hermitian matrix, which had 1024 diagonal blocks and the size of each block was 128 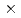128 within a second.
Shiraishi, Junya; Tokuda, Shinji; Aiba, Nobuyuki
Physics of Plasmas, 17(1), p.012504_1 - 012504_9, 2010/01
Times Cited Count：8 Percentile：30.63(Physics, Fluids & Plasmas)The classical matching problem for magnetohydrodynamic stability analysis is revisited to study effects of the plasma flow on the resistive wall modes (RWMs). The Newcomb equation, which describes the marginal states and governs the regions except for the resonant surface, is generalized to analyze the stability of flowing plasmas. When there exists no flow, the singular point of the Newcomb equation and the resonant surface degenerate into the rational surface. The location of the rational surface is prescribed by the equilibrium, hence the inner layer, which must contain the resonant surface, can be set a priori. When the flow exists, the singular point of the Newcomb equation splits in two due to the Doppler shift. Additionally, the resonant surface deviates from the singular points and the rational surface if the resonant eigenmode has a real frequency. Since the location of the resonant surface depends on the unknown real frequency, it can be determined only a posteriori. Hence the classical asymptotic matching method cannot be applied. This paper shows that a new matching method that generalizes the asymptotic one to use the inner layer with finite width works well for the stability analysis of flowing plasmas. If the real frequency is limited in a certain range such as the RWM case, the resonance occurs somewhere in the finite region around the singular points, hence the inner layer with finite width can capture the resonant surface.
Kushida, Noriyuki; Takemiya, Hiroshi; Tokuda, Shinji
Proceedings of International Conference for High Performance Computing, Networking, Storage and Analysis (SC '09) (USB Flash Drive), 2 Pages, 2009/11
In this study, we developed a high speed eigenvalue solver that is the necessity of plasma stability analysis system for International Thermo-nuclear Experimental Reactor (ITER) on Cell cluster system. Our stability analysis system is developed in order to prevent the damage of the ITER from the plasma disruption. The stability analysis system requires solving the eigenvalue of matrices whose dimension is hundred thousand in a few seconds. However, current massively parallel processor (MPP) type supercomputer is not applicable for such short-term calculation, because of the network overhead become dominant. Therefore, we employ Cell cluster system, because we can obtain sufficient processing power with small number of processors. Finally, we succeeded to solve the block tri-diagonal Hermitian matrix, which had 1024 diagonal blocks and each block size was 128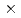128, within one second.
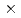B flowMiyato, Naoaki; Scott, B. D.*; Strintzi, D.*; Tokuda, Shinji
Journal of the Physical Society of Japan, 78(10), p.104501_1 - 104501_13, 2009/10
Times Cited Count：28 Percentile：76.99(Physics, Multidisciplinary)A modified guiding-centre fundamental 1-form with strong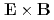 
flow is derived by the phase space Lagrangian Lie perturabtion method. Since the symplectic part of the derived 1-form is the same as the standard one without the strong 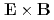flow, it yields the standard Lagrange and Poisson brackets. Therefore the guiding-centre Hamilton equations keep their general form even when temporal evolution of the 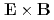flow is allowed. Compensation of keeping the standard symplectic structure is paid by complication of the guiding-centre Hamiltonian. However it is possible to simplify the Hamiltonian in well localised transport barrier regions like a tokamak H-mode edge and an internal transport barrier in a reversed shear tokamak. The guiding-centre Vlasov and Poisson equations are derived from the variational principle. The conserved energy of the system is obtained from the Noether's theorem.
Tokuda, Shinji
Journal of Plasma and Fusion Research SERIES, Vol.8, p.1176 - 1178, 2009/09
The conjugate variable method is discussed in order that the Hamilton-Lie perturbation theory becomes applicable to ordinary differential equations that appear in plasma physics. The method is used to the analysis of charged particle motion in a magnetic field, and to the reduced MHD (MagnetoHydroDynamic) equations to derive a canonical 1-form of them. The 1-form thus obtained provides the initial step for the application of the Hamilton-Lie perturbation theory.
Ozeki, Takahisa; Hayashi, Nobuhiko; Honda, Mitsuru; Aiba, Nobuyuki; Hamamatsu, Kiyotaka; Shimizu, Katsuhiro; Kawashima, Hisato; Hoshino, Kazuo; Takizuka, Tomonori; Tokuda, Shinji
Journal of Plasma and Fusion Research SERIES, Vol.8, p.1138 - 1142, 2009/09
Aiba, Nobuyuki; Tokuda, Shinji; Furukawa, Masaru*; Snyder, P. B.*; Chu, M. S.*
Computer Physics Communications, 180(8), p.1282 - 1304, 2009/08
Times Cited Count：31 Percentile：81.89(Computer Science, Interdisciplinary Applications)A new linear MHD stability code MINERVA is developed for investigating a toroidal rotation effect on the stability of ideal MHD modes in tokamak plasmas. This code solves the Frieman-Rotenberg equation as not only the generalized eigenvalue problem but also the initial value problem. The parallel computing method used in this code realizes the stability analysis of both long and short wavelength MHD modes in short time. The results of some benchmarking tests show the validity of this MINERVA code. The numerical study with MINERVA about the toroidal rotation effect on the edge MHD stability shows that the rotational shear destabilizes the long/intermediate wavelength modes but stabilizes the short wavelength edge localized MHD modes, though the rotation frequency destabilizes both the long and the short wavelength MHD modes.
Aiba, Nobuyuki; Tokuda, Shinji; Furukawa, Masaru*; Oyama, Naoyuki; Ozeki, Takahisa
Nuclear Fusion, 49(6), p.065015_1 - 065015_9, 2009/06
Times Cited Count：25 Percentile：67.18(Physics, Fluids & Plasmas)Effects of a toroidal rotation are investigated numerically on the stability of the MHD modes in the tokamak edge pedestal, which relate to the type-I edge-localized mode (ELM). A linear MHD stability code MINERVA is newly developed for solving the Frieman-Rotenberg equation that is the linear ideal MHD equation with flow. Numerical stability analyses with this code reveal that the sheared toroidal rotation destabilizes edge localized MHD modes, and this rotation effect becomes stronger as the toroidal mode number of the unstable MHD mode increases in case that the toroidal mode number is smaller than 40. Since the toroidal mode number of the unstable MHD mode strongly depends on the safety factor profile, the destabilizing effect of the toroidal rotation is affected by the safety factor profile. The sheared toroidal rotation also has an impact on the mode structure of the edge localized MHD mode, and the mode structure can become narrower as the toroidal rotation increases.
