Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
植木 太郎
Proceedings of 12th International Conference on Nuclear Criticality Safety (ICNC2023) (Internet), 9 Pages, 2023/10
モンテカルロ法ソルバーSolomonは、C++14標準で記述されたオブジェクト指向の中性子輸送計算コードである。Solomonは、通常の臨界安全解析機能と乱雑化媒質の臨界性評価機能で構成されており、後者に関して、不完全確率的乱雑化ワイエルシュトラス関数(IRWF)による乱雑化媒質のクラスが装備されている。このため、乱雑化媒質の臨界性揺らぎを、多数のIRWFレプリカを生成して、レプリカ毎に臨界計算を実施することにより評価できる。一方で、必要とされるIRWFレプリカ数を事前に知ることは不可能である。この問題への対処のため、Solomonに、乱雑化増幅機能を装備した。具体的には、オン-オフ型への有界増幅をIRWFレプリカに適用することにより、中性子実効増倍率の上限値推定に関して、レプリカ生成数の95%以上の削減が可能となる。また、Solomonには、ボクセル重ね合わせ機能も装備されている。この機能の有望な応用として、ステンレス鋼(SUS304)中の鉄同位体による共鳴吸収反応の評価例を示す。
須山 賢也; 植木 太郎; 郡司 智; 渡邉 友章; 荒木 祥平; 福田 航大; 山根 祐一; 井澤 一彦; 長家 康展; 菊地 丈夫; et al.
Proceedings of 12th International Conference on Nuclear Criticality Safety (ICNC2023) (Internet), 6 Pages, 2023/10
2011年の福島第一原子力発電所の事故により発生した燃料デブリの臨界安全性評価において採用される手法の妥当性を臨界実験で得られたデータに基づいて検証するため、NRAからの委託により原子力機構は2014年から関連研究開発プロジェクトを実施している。このプロジェクトにおいては、i)燃料デブリの臨界特性の網羅的計算とデータベース化(燃料デブリ臨界マップの開発)、ii)新しい連続エネルギーモンテカルロコードの開発、iii)臨界事故の評価、iv)臨界安全性評価手法の検証実験のための臨界集合体STACYの改良などが行われている。前回のICNC2019以降、本プロジェクトは2024年5月に正式運転を開始するSTACYの改造やパワースペクトルに準拠した空間ランダム分布を持つ物質の臨界計算に適したモンテカルロコード「Solomon」の開発で大きな進展があった。本発表では、この研究開発プロジェクトの全体像と各技術トピックの状況について紹介する。
須山 賢也; 植木 太郎; 郡司 智; 渡邉 友章; 荒木 祥平; 福田 航大
Proceedings of 20th International Symposium on the Packaging and Transportation of Radioactive Materials (PATRAM22) (Internet), 5 Pages, 2023/06
1990年代以降計算機能力が向上して連続エネルギーモンテカルロコードが広く使用されるようになってから、どのような複雑な体系であっても必要なときに高精度な臨界計算が可能となり、臨界安全評価におけるハンドブック類の存在意義は大きく変化した。大量の計算をあらかじめ行ってデータを整理しておくことの価値は低下したため、1999年に第2版が公刊されて以降、過去四半世紀近く我が国では臨界安全ハンドブックの改訂は行われて来なかった。2011年に福島第一原子力発電所事故が発生した我が国では、複雑な構成元素を含む燃料デブリの輸送や貯蔵における臨界安全問題を取り扱う必要に迫られており、そのような複雑な物質の臨界安全管理のためのデータの整理が喫緊の課題となっている。また、燃焼度クレジットの分野では、事故の影響のために到達燃焼度の低い燃料集合体の輸送や貯蔵も課題となる。そして、連続エネルギーモンテカルロコードの入力となる核データは1990年代から数回改訂されてJENDL-5が2021年末から利用できるようになるなど、その取り入れも現場のニーズとして上がってきている。本報告では我が国における最新の臨界安全研究の概要と、輸送や貯蔵分野に適用することも可能な我が国における臨界安全ハンドブックの改訂計画について報告する。
植木 太郎
Progress in Nuclear Energy, 159, p.104630_1 - 104630_9, 2023/05
被引用回数:0 パーセンタイル:0.01(Nuclear Science & Technology)一般化極値(GEV)は、極端な値の観測に関する統計モデルである。本論文では、GEVの方法論を、サンプリングの困難さで知られる弱結合体系のモンテカルロ臨界計算の例題に適用し、中性子実効増倍率(keff)分布の裾野の利用価値を評価したことを報告する。具体的には、核分裂源サイクルあたりの粒子数が十分に大きい場合に、keff分布の上限と下限に対する極値指数(EVI)が不確かさの範囲内で同じ値をとること、及びその値が境界値層としてのガンベル分布のEVIを含むワイブル分布の範囲内に収まることを示す。核分裂源サイクルあたりの粒子数が不十分な場合に対しては、一つの平衡状態から別の平衡状態への移行時に、keff分布の上下限のEVIが剥離し、一方がワイブル分布の範囲内に、もう一方がフレシェ分布の範囲内に入り、計算の異常診断に利用可能であることが示される。
植木 太郎
Progress in Nuclear Energy, 144, p.104099_1 - 104099_7, 2022/02
被引用回数:0 パーセンタイル:0.01(Nuclear Science & Technology)確率的乱雑化ワイエルシュトラス関数(RWF: randomized Weierstrass function)は、無秩序な物質混合で生成する乱雑化媒質の臨界性不確かさ評価のための手法である。本論文は、実用面でのRWFの精緻化を、周波数領域変数の上下限指定を伴うスペクトル範囲制御により達成したことを報告する。臨界解析実務への具体的効果は、空間分布が不確定な燃料デブリを想定した乱雑化媒質に対して、逆冪乗則パワースペクトルの下での公平な臨界性不確かさ評価を可能にすることである。数学的側面においては、RWFの三角関数項の無限和が、任意の低周波数領域を含むように拡張され、スペクトル範囲制御という唯一の目的のために有限項に切り捨てられている。これは、精緻化RWFが、ワイエルシュトラス関数のフラクタル特性への収束の問題と切り離されたことを意味する。このため、精緻化RWFは、不完全確率的乱雑化ワイエルシュトラス関数(IRWF: Imcomplete RWF)と命名される。適用事例として、3次元化されたIRWFを、中性子減速環境下の3種燃料から成る乱雑化燃料混合体に適用して中性子実効増倍率の不確かさをモンテカルロ法コードSolomonにより評価したことを報告する。
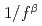 random media
random media荒木 祥平; 山根 祐一; 植木 太郎; 外池 幸太郎
Nuclear Science and Engineering, 195(10), p.1107 - 1117, 2021/10
被引用回数:2 パーセンタイル:31.78(Nuclear Science & Technology)燃料デブリのように乱雑な性状をもつ核燃料物質の臨界管理は事故後の安全対策において重要な課題のひとつである。様々な乱雑で管理されていない自然現象を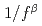 ノイズを用いて記述できることから、乱雑な性状をもつ核燃料物質についても
ノイズを用いて記述できることから、乱雑な性状をもつ核燃料物質についても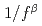 スペクトル分布を持つモデルが適用可能と考えた。本研究では、
スペクトル分布を持つモデルが適用可能と考えた。本研究では、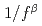 モデルで表現される核燃料物質について、中性子実効増倍率と減速条件の関係を検討した。減速条件の指標としてコンクリートと核燃料物質の体積比を定めた上で、乱雑化ワイエルストラス関数(RWF)に基づく
モデルで表現される核燃料物質について、中性子実効増倍率と減速条件の関係を検討した。減速条件の指標としてコンクリートと核燃料物質の体積比を定めた上で、乱雑化ワイエルストラス関数(RWF)に基づく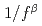 スペクトル分布を持つモデルから多数の乱雑性状を生成した。生成された各々の乱雑性状について、2群エネルギーモンテカルロ計算により増倍率を計算し、結果を分散,歪み度,尖り度を用いて整理した。これらの統計量は最適減速条件において極値を持つことが見出された。また、
スペクトル分布を持つモデルから多数の乱雑性状を生成した。生成された各々の乱雑性状について、2群エネルギーモンテカルロ計算により増倍率を計算し、結果を分散,歪み度,尖り度を用いて整理した。これらの統計量は最適減速条件において極値を持つことが見出された。また、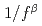 モデルで表現される核燃料物質について、増倍率の分布範囲、分布の歪み、外れ値の出現を推定できる可能性が示唆された。
モデルで表現される核燃料物質について、増倍率の分布範囲、分布の歪み、外れ値の出現を推定できる可能性が示唆された。
植木 太郎
Nuclear Science and Engineering, 195(2), p.214 - 226, 2021/02
被引用回数:5 パーセンタイル:53.85(Nuclear Science & Technology)極端な無秩序の下では、物理的な力学系は、逆冪乗則パワースペクトルで特徴づけられる状態に落ち着く。本論文は、このような無秩序状態の乱雑系に関して、ホワイトノイズを含む形へのワイエルシュトラス関数モデルの拡張および多種物質混合方式の開発を報告する。具体的な逆冪乗則パワースペクトルの式および多種物質系でも計算機上で実現可能な混合手順を提示する。SOLOMONモンテカルロソルバーおよびJENDL-4核データーライブラリを使用した数値計算例についても報告する。
植木 太郎
Nuclear Science and Engineering, 194(6), p.422 - 432, 2020/06
被引用回数:0 パーセンタイル:0.01(Nuclear Science & Technology)モンテカルロ臨界計算におけるタリー平均値の分布収束は、自己相関係数減衰の観点から判定可能である。ただし、大きなラグ(世代差)での統計量の不確かさは大きく、標本自己相関係数の減衰評価に基づくアプローチは現実的でない。本論文は、この課題に対処するなめの汎用的な解決法を提供する。具体的には、タリーの標準化時系列を、確率微分方程式に基き、ブラウン運動に分布収束する時系列に変換する。ブラウン運動においては、期待値がゼロで差分が独立である。この性質を利用して、タリー平均値の分布収束判定法が構成される。判定基準の閾値は、スペクトル解析により決められる。この判定法の有効性は、極端に強相関な例題と標準的な例題に対して、連続エネルギーモンテカルロ計算により示される。
 on effective multiplication factor in 1/f
on effective multiplication factor in 1/f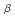 spectrum random system
spectrum random system荒木 祥平; 山根 祐一; 植木 太郎; 外池 幸太郎
Proceedings of International Conference on the Physics of Reactors; Transition To A Scalable Nuclear Future (PHYSOR 2020) (USB Flash Drive), 8 Pages, 2020/03
本研究は1/f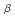 ノイズモデルに従う乱雑化体系の実効増倍率に対する
ノイズモデルに従う乱雑化体系の実効増倍率に対する の影響を調査したものである。2群のモンテカルロ計算を用いて乱雑体系の増倍率を計算し、1/f
の影響を調査したものである。2群のモンテカルロ計算を用いて乱雑体系の増倍率を計算し、1/f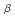 乱雑体系の空間分布の非均一さが
乱雑体系の空間分布の非均一さが とともに増加するため、増倍率分布の標準偏差が
とともに増加するため、増倍率分布の標準偏差が とともに増加することを明らかにした。
とともに増加することを明らかにした。
長家 康展; 植木 太郎; 外池 幸太郎
Proceedings of 11th International Conference on Nuclear Criticality Safety (ICNC 2019) (Internet), 9 Pages, 2019/09
燃料デブリ体系に対する臨界安全解析のために新規モンテカルロ計算ソルバーSolomonを開発した。Solomonは、通常の臨界安全解析だけでなく、燃料デブリを含む損傷した原子炉の炉心の臨界安全解析もできるように設計されている。本論文では、Solomon開発の現状について述べ、乱雑化ワイエルシュトラス関数モデル, ボクセル形状を重ね合わせた乱雑化ワイエルシュトラス関数モデルの応用について紹介する。
植木 太郎
Nuclear Science and Engineering, 193(7), p.776 - 789, 2019/07
被引用回数:5 パーセンタイル:48.99(Nuclear Science & Technology)相関を伴うモンテカルロ計算タリーの統計誤差を、標準化時系列とブラウン橋の統計を組み合わせて評価できることは、オペレーションズ・リサーチで知られている事実である。本論文では、標準化時系列を確率微分方程式に基づいてブラウン運動に収束する統計量に変換し、統計誤差評価・確率的分布収束の判定を、近似なしで、タリーを格納することなしに実行する手法について報告する。手法の妥当性検証に関しては、強相関下の臨界性問題、原子炉の全炉心計算、動特性パラメータ評価を例として報告する。
植木 太郎
Proceedings of International Conference on Mathematics and Computational Methods applied to Nuclear Science and Engineering (M&C 2019) (CD-ROM), p.151 - 160, 2019/00
物理・力学的な系は、極端な無秩序の下で、逆冪乗則パワースペクトルの状態に進展していくことが知られている。本著者は、確率的乱雑化ワイエルシュトラス関数による広範な逆冪乗則パワースペクトルの模擬を検討し、乱雑化無秩序媒質のモデル機能を、連続エネルギーモンテカルロ法ソルバーのデルタ追跡法を用いて検証した。数値計算例として、国際臨界安全ベンチマーク評価プロジェクトのTopsy炉心に基づく乱雑化体系の臨界性評価の揺らぎについて報告する。
植木 太郎
Journal of Nuclear Science and Technology, 55(10), p.1180 - 1192, 2018/10
被引用回数:4 パーセンタイル:38.58(Nuclear Science & Technology)確率的に乱雑化された媒質のモンテカルロ法中性子輸送計算は、臨界性の揺らぎ評価に有効である。ところが、無限に広がる正規分布の裾野を、体積割合の上限と下限のような0%と100%の間に収めるために切り捨ててしまうと、正規性が失われてしまう。そこで、本研究においては、確率過程のKarhunen-Loeve展開による重ね合わせブラウン運動の近似と、確率解析におけるブラウン運動の反射軌道の等価性に基づき、空間的に一定の分散で有界の範囲に収まる正規分布駆動の乱雑化手法を開発した。ウラン燃料・コンクリート・ステンレス鋼への適用を通して、当該手法による効率的な臨界計算が可能であることを示した。
植木 太郎
Journal of Nuclear Science and Technology, 54(12), p.1310 - 1320, 2017/12
被引用回数:6 パーセンタイル:51.46(Nuclear Science & Technology)モンテカルロ法臨界計算での実効増倍率・燃料集合体出力等の信頼区間算出においては、中心極限定理に基づくタリー標準化関数の分布収束の判定が根本的に重要である。この課題に対処するため、タリー標準化関数のパワースペクトル評価手法を開発したことを報告する。具体的には、タリー標準化関数のブラウン橋への分布収束により、タリー標準化関数のパワースペクトルが周波数の逆2乗則分布に収束することを導出し、パワースペクトルの対数分布の勾配の算出を通して分布収束を診断できることを示した。また、分布収束の不十分さを、非整数ブラウン運動モデルにより評価できることも示した。本開発手法の妥当性を、加圧水型軽水炉の局所出力および燃料・コンクリート系デブリモデルを例として、検証した。
植木 太郎
Proceedings of International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering (M&C 2017) (USB Flash Drive), 6 Pages, 2017/04
モンテカルロ法臨界計算においては、中性子輸送計算と核分裂源生成の繰り返しによって生み出されたタリー時系列に、中心極限定理を適用し、信頼区間を算出する。このため、タリー標準化時系列関数の分布収束の判定が、計算結果の統計的信頼性担保のための課題である。本国際会議論文において、標準化時系列関数のパワースペクトルを診断し、分布収束を判定する手法の開発を報告する。数値計算例としては、ウラン・コンクリート系燃料デブリの臨界性評価への適用を報告する。
植木 太郎
Journal of Nuclear Science and Technology, 54(3), p.267 - 279, 2017/03
被引用回数:8 パーセンタイル:61.27(Nuclear Science & Technology)過酷事故の炉心溶融の際に生成される二酸化ウラン・コンクリート混合物の臨界性評価に関連して、ワイエルシュトラス関数に基づく確率論的乱雑化モデルを構築し、モンテカルロ法臨界計算の不確かさを検討した。中性子実効増倍率の評価値には、無視できない揺らぎが生じることがわかった。
植木 太郎
Journal of Nuclear Science and Technology, 53(3), p.312 - 322, 2016/03
被引用回数:7 パーセンタイル:55.03(Nuclear Science & Technology)モンテカルロ法臨界計算では、平衡核分裂源分布が、世代間の自己相関の影響下にある。したがって、自己相関の観点から、世代の繰り返し数の充分さを判断することが必要とされている。一方、各世代の計算値と世代間平均値との差を標準偏差でスケーリングして構成される標準化時系列関数は、中心極限定理上の収束に伴い、自己相関の度合いに関係なく、ブラウン運動の有効統計量であるブラウン橋に収束することが知られている。本論文は、標準化時系列関数のフラクタル次元をブラウン橋のフラクタル次元と比較することにより、中心極限定理上の収束の達成度を診断できることを報告する。加圧水型原子炉の出力分布問題およびMennerdahl氏により提唱された臨界問題に関して、診断例を報告する。
植木 太郎
Journal of Nuclear Science and Technology, 50(8), p.762 - 773, 2013/08
被引用回数:4 パーセンタイル:32.48(Nuclear Science & Technology)確率論におけるブラウン運動の理論から導かれるブラウン橋の手法は、相関を伴うモンテカルロ法計算結果の統計誤差評価に有効であることが知られている。そこで、本研究では、ブラウン橋に基づく繰り返し積分法による統計誤差評価手法を開発した。性能評価を電気出力1200MWの加圧水型原子炉の出力分布計算において実施したところ、3次元炉心内のほとんどの位置において、標準偏差の評価値のバイアスが無視できることが確認された。実用化に向けての課題が安定性のみであることが示された。
植木 太郎
Journal of Nuclear Science and Technology, 49(12), p.1134 - 1143, 2012/12
被引用回数:11 パーセンタイル:63.41(Nuclear Science & Technology)極端な条件下でのモンテカルロ法臨界計算について、世代間自己相関の観点から、評価量バイアスの存在可能性,判定方法、及び修正方法を示した。
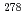 113 of the 113th element
113 of the 113th element森田 浩介*; 森本 幸司*; 加治 大哉*; 羽場 宏光*; 大関 和貴*; 工藤 祐生*; 住田 貴之*; 若林 泰生*; 米田 晃*; 田中 謙伍*; et al.
Journal of the Physical Society of Japan, 81(10), p.103201_1 - 103201_4, 2012/10
被引用回数:167 パーセンタイル:97.27(Physics, Multidisciplinary)113番元素である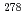 113を
113を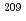 Bi標的に
Bi標的に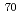 Znビームを照射する実験により合成した。観測したのは6連鎖の
Znビームを照射する実験により合成した。観測したのは6連鎖の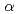 崩壊で、そのうち連鎖の5番目と6番目は既知である
崩壊で、そのうち連鎖の5番目と6番目は既知である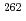 Db及び
Db及び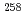 Lrの崩壊エネルギーと崩壊時間と非常によく一致した。この意味するところは、その連鎖を構成する核種が
Lrの崩壊エネルギーと崩壊時間と非常によく一致した。この意味するところは、その連鎖を構成する核種が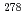 113,
113, 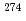 Rg (Z=111),
Rg (Z=111), 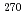 Mt (Z=109),
Mt (Z=109), 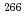 Bh (Z=107),
Bh (Z=107), 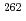 Db (Z=105)及び
Db (Z=105)及び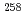 Lr (Z=103)であることを示している。本結果と2004年, 2007年に報告した結果と併せて、113番元素である
Lr (Z=103)であることを示している。本結果と2004年, 2007年に報告した結果と併せて、113番元素である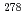 113を曖昧さなく生成・同定したことを強く結論付ける結果となった。
113を曖昧さなく生成・同定したことを強く結論付ける結果となった。