Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Nakano, Tomohide; Asakura, Nobuyuki; Takenaga, Hidenobu; Kubo, Hirotaka; Miura, Yukitoshi; Shimizu, Katsuhiro; Konoshima, Shigeru; Masaki, Kei; Higashijima, Satoru; JT-60 Team
Nuclear Fusion, 46(5), p.626 - 634, 2006/05
Times Cited Count:21 Percentile:55.94(Physics, Fluids & Plasmas)In order to understand plasma-wall interactions in a long time scale, the discharge pulse length has been extended from 15 s to 65 s, with the NB-heating duration extended to 30 s. Nearly-saturation of the divertor plates was observed in the latter half of long pulse ELMy H-mode discharges. Particle sink into the divertor plates gradually decreased, and subsequently, wall-pumping efficiency became zero. This wall saturation resulted in a rise of the main plasma density without any auxiliary particle supply besides NB with divertor-pumping. Even when the total injected energy reached up to 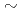 350 MJ in a discharge, neither sudden increase of carbon generation such as carbon bloom nor increase of the dilution of the main plasma was observed.
350 MJ in a discharge, neither sudden increase of carbon generation such as carbon bloom nor increase of the dilution of the main plasma was observed.
Ido, Takeshi*; Miura, Yukitoshi; Hoshino, Katsumichi; Kamiya, Kensaku; Hamada, Yasuji*; Nishizawa, Akimitsu*; Kawasumi, Yoshiaki*; Ogawa, Hiroaki; Nagashima, Yoshihiko*; Shinohara, Koji; et al.
Nuclear Fusion, 46(5), p.512 - 520, 2006/05
Times Cited Count:87 Percentile:92.32(Physics, Fluids & Plasmas)The electrostatic fluctuation spectrum and the fluctuation-induced particle flux of the JFT-2M tokamak were estimated using the hevy ion beam probe (HIBP) measurement. A geodesic acoustic mode (GAM) of the frequency about15kHz was identified in the L-mode. The GAM has its peak at about 3cm inside of the separatrix with the electric field of about 1.4kV/m. The estimated turbulent particle flux is found to be intermittent. It is found that the density fluctuation is modulated by the GAM in the wide frequency range and the coherence analysis shows that the flucruation-induced particle flux is partially contributed by the GAM. In the H-mode the GAM disappears and the fluctuation and the flux is much decreased.The mechanism of the large burst-like flux in the L-mode is not understood yet and left as the future problem.
Kamiya, Kensaku; Kawashima, Hisato; Ido, Takeshi*; Oyama, Naoyuki; Bakhtiari, M.*; Kasai, Satoshi; Kusama, Yoshinori; Miura, Yukitoshi; Ogawa, Hiroaki; Tsuzuki, Kazuhiro; et al.
Nuclear Fusion, 46(2), p.272 - 276, 2006/02
Times Cited Count:3 Percentile:10.32(Physics, Fluids & Plasmas)An attractive operational regime without any large ELMs, namely High Recycling Steady (HRS) H-mode, was found on JFT-2M during Y2000 campaign after boronization. Recent experiments have concentrated on the studies of the access conditions for the HRS regime, in terms of the pedestal parameters. The HRS regime was more likely at higher edge density and lower edge temperature, which corresponds to the normalized electron collisionality of 1 in the plasma edge region.
Ushigome, Masahiro*; Ide, Shunsuke; Ito, Satoshi*; Jotaki, Eriko*; Mitarai, Osamu*; Shiraiwa, Shunichi*; Suzuki, Takahiro; Takase, Yuichi*; Tanaka, Shigetoshi*; Fujita, Takaaki; et al.
Nuclear Fusion, 46(2), p.207 - 213, 2006/02
Times Cited Count:12 Percentile:38.27(Physics, Fluids & Plasmas)This papaer studies on tokamak plasma start-up completely without central solenoid (CS). On the JT-60 tokamak it is demonstrated that a completely CS-less Ip start-up to 100 kA was achieved even without any null-point by Electron cyclotron range of frequencies (ECRF) and outer PF coil current swing only. Necessary conditions (the EC power, the toroidal field etc.) were clarified. Moreover, it was succeded to maintain Ip = 260kA for 1 sec without CS by NB only. In addition Ip ramp-up by EC and NB only (without LHCD) from 215 to 310kA was achieved. In a high confinement reversed shear discharge, a result suggesting bootstrap over drive was obtained.
Ishikawa, Masao; Takechi, Manabu; Shinohara, Koji; Kusama, Yoshinori; Cheng, C. Z.*; Matsunaga, Go; Todo, Yasushi*; Gorelenkov, N. N.*; Kramer, G. J.*; Nazikian, R. M.*; et al.
Nuclear Fusion, 45(12), p.1474 - 1480, 2005/12
Times Cited Count:38 Percentile:73.45(Physics, Fluids & Plasmas)To investigate energetic ion transport induced by Alfven eigenmodes (AEs) the neutron emission profile measurement and the charge exchange (CX) neutral particle flux measurement by Natural Diamond Detector has been performed simultaneously in the JT-60U for the first time. The energetic ion profiles inferred from these measurements indicate that ALEs cause a radial redistribution of energetic ions of limited energy range from the core region to the outer region of the plasma in weak shear plasmas. This energy range is consistent with the resonance condition between the mode and the energetic ions. In reversed shear plasmas, reversed-shear-induced AEs (RSAEs) and their transition to TAEs as the minimum value of the safety factor decreases has been observed. Neutron measurements suggest energetic ion loss is large in the transition phase from RSAEs to TAEs.
Takechi, Manabu; Fujita, Takaaki; Ishii, Yasutomo; Ozeki, Takahisa; Suzuki, Takahiro; Isayama, Akihiko; JT-60 Team
Nuclear Fusion, 45(12), p.1694 - 1699, 2005/12
Times Cited Count:7 Percentile:24.05(Physics, Fluids & Plasmas)High performance reversed shear discharges with strong internal transport barrier (ITB) and flat pressure profile in the plasma core region disrupt frequently even with low beta. We analyzed MHD instabilities leading to low beta disruption with measuring fluctuations and current profile with MSE measurement. We mainly observed two type of disruptions. One is the disruption without precursor at 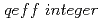 . The other is the disruption with n=1 precursor of
. The other is the disruption with n=1 precursor of 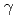
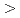 100 ms. To explain these characteristics of disruption, we introduce the simple model such as, disruption occurs when the both MHD instabilities at plasma surface and at safety factor being equal to surface mode are unstable. This simple model can explain almost all observed disruption by two process. One is the surface mode triggered disruption, which occurs when qeff change, corresponding q surface at ITB layer changes discretely. The other is the internal mode triggered disruption, which occurs when corresponding q surface become unstable gradually.
100 ms. To explain these characteristics of disruption, we introduce the simple model such as, disruption occurs when the both MHD instabilities at plasma surface and at safety factor being equal to surface mode are unstable. This simple model can explain almost all observed disruption by two process. One is the surface mode triggered disruption, which occurs when qeff change, corresponding q surface at ITB layer changes discretely. The other is the internal mode triggered disruption, which occurs when corresponding q surface become unstable gradually.
Idomura, Yasuhiro; Tokuda, Shinji; Kishimoto, Yasuaki
Nuclear Fusion, 45(12), p.1571 - 1581, 2005/12
Times Cited Count:43 Percentile:76.88(Physics, Fluids & Plasmas)Using a global gyrokinetic toroidal particle code, the toroidal electron temperature gradient driven (ETG) turbulence is studied in positive and reversed shear tokamaks. In the nolinear turbulent state, the ETG turbulence in the positive and reversed shear configurations show quite different structure formations. In the positive shear configuration, the ETG turbulence is dominated by streamers which have a ballooning type structure, and the electron temperature 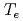 profile is quickly relaxed to the marginally stable state in a turbulent time scale. In the reversed shear configuration, quasi-steady zonal flows are produced in the regative shear region, while the positive shear region is characterized by streamers. Accordingly, the electron thermal diffusivity
profile is quickly relaxed to the marginally stable state in a turbulent time scale. In the reversed shear configuration, quasi-steady zonal flows are produced in the regative shear region, while the positive shear region is characterized by streamers. Accordingly, the electron thermal diffusivity 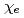 has a gap structure across the
has a gap structure across the 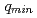 surface, and the
surface, and the 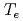 gradinet is sustained above the marginal value for a long time in the quasi-steady phase. The results suggest a stiffness of the
gradinet is sustained above the marginal value for a long time in the quasi-steady phase. The results suggest a stiffness of the 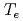 profile in positive shear tokamaks, and a possibility of the Te transport barrier in reversed shear tokamaks.
profile in positive shear tokamaks, and a possibility of the Te transport barrier in reversed shear tokamaks.
Kizu, Kaname; Miura, Yushi*; Tsuchiya, Katsuhiko; Ando, Toshinari*; Koizumi, Norikiyo; Matsui, Kunihiro*; Sakasai, Akira; Tamai, Hiroshi; Matsukawa, Makoto; Ishida, Shinichi; et al.
Nuclear Fusion, 45(11), p.1302 - 1308, 2005/11
Times Cited Count:4 Percentile:13.77(Physics, Fluids & Plasmas)no abstracts in English
Oikawa, Toshihiro; Suzuki, Takahiro; Isayama, Akihiko; Hayashi, Nobuhiko; Fujita, Takaaki; Naito, Osamu; Tsuda, Takashi; Kurita, Genichi; JT-60 Team
Nuclear Fusion, 45(9), p.1101 - 1108, 2005/09
Times Cited Count:4 Percentile:13.77(Physics, Fluids & Plasmas)Evolution of the current density profile associated with magnetic island formation in a neoclassical tearing mode plasma was measured for the first time in JT-60U by. As the island grew, the current density profile turned flat at the radial region of the island, followed by an appearance of a hollow structure. As the island shrank, the deformed region became narrower, and it finally diminished after the disappearance of the island. In an MHD-quiescent plasma, on the other hand, no deformation was observed. The observed deformation in the current density profile associated with the tearing mode is reproduced in a time dependent transport simulation assuming reduction of the bootstrap current in the radial region of the island. Comparison of the measurement with a calculated steady-state solution also explains the temporal behaviors of the current density and safety factor profiles with reduction and recovery of the bootstrap current. From the experimental observation and simulations, we reach conclusion that the bootstrap current decreases within the island O-point.
Oyama, Naoyuki; Sakamoto, Yoshiteru; Isayama, Akihiko; Takechi, Manabu; Gohil, P.*; Lao, L. L.*; Snyder, P. B.*; Fujita, Takaaki; Ide, Shunsuke; Kamada, Yutaka; et al.
Nuclear Fusion, 45(8), p.871 - 881, 2005/08
Times Cited Count:124 Percentile:95.09(Physics, Fluids & Plasmas)The grassy ELM is characterized by the high frequency periodic collapse up to 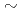 kHz, which is
kHz, which is 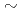 15 times faster than that for type I ELM. A divertor peak heat flux due to grassy ELMs is less than 10% of that for type I ELMs. This smaller heat flux is caused by narrower radial extent of the collapse of temperature pedestal. The different radial extent between type I ELMs and grassy ELMs qualitatively agrees with the different radial distribution of the eigen function of the ideal MHD stability analysis. The ratio of ELM energy loss for grassy ELMs to the pedestal stored energy was 0.4-1%. In high triangularity regime, ELM amplitude, frequency and type can be changed from type I ELM to high frequency grassy ELM as counter plasma rotation was increased. In low triangularity regime, on the other hand, the complete ELM suppression (QH-mode) has been achieved, when the plasma position is optimized with CTR-NBIs. The existence of the edge fluctuations localized in pedestal region may reduce the pedestal pressure, and therefore the QH-mode can be sustained for long time up to 3.4s.
15 times faster than that for type I ELM. A divertor peak heat flux due to grassy ELMs is less than 10% of that for type I ELMs. This smaller heat flux is caused by narrower radial extent of the collapse of temperature pedestal. The different radial extent between type I ELMs and grassy ELMs qualitatively agrees with the different radial distribution of the eigen function of the ideal MHD stability analysis. The ratio of ELM energy loss for grassy ELMs to the pedestal stored energy was 0.4-1%. In high triangularity regime, ELM amplitude, frequency and type can be changed from type I ELM to high frequency grassy ELM as counter plasma rotation was increased. In low triangularity regime, on the other hand, the complete ELM suppression (QH-mode) has been achieved, when the plasma position is optimized with CTR-NBIs. The existence of the edge fluctuations localized in pedestal region may reduce the pedestal pressure, and therefore the QH-mode can be sustained for long time up to 3.4s.
Inoue, Takashi; Taniguchi, Masaki; Morishita, Takatoshi; Dairaku, Masayuki; Hanada, Masaya; Imai, Tsuyoshi*; Kashiwagi, Mieko; Sakamoto, Keishi; Seki, Takayoshi*; Watanabe, Kazuhiro
Nuclear Fusion, 45(8), p.790 - 795, 2005/08
The R&D of a 1 MeV accelerator and a large negative ion source have been carried out at JAERI. The paper presents following progress as a step toward ITER NB system. (1) Accelerator R&D: According to success in improvement of voltage holding capability, the acceleration test of H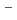 ions up to 1 MeV class energy is in progress. H
ions up to 1 MeV class energy is in progress. H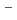 ion beams of 1 MeV, 100 mA class have been generated with a substantial beam current density (100 A/m
ion beams of 1 MeV, 100 mA class have been generated with a substantial beam current density (100 A/m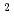 ), and the current density is still increasing by the ion source tuning. (2) Large ion source R&D: One of major causes that limited the NB injection performance was spatial unifomity of negative ion production in existing negative-ion based NB systems. The present study revealed that the negative ions produced in the extraction region of the source were locally destructed by fast electrons leaking through magnetic filter. Some countermeasures and their test results are also described.
), and the current density is still increasing by the ion source tuning. (2) Large ion source R&D: One of major causes that limited the NB injection performance was spatial unifomity of negative ion production in existing negative-ion based NB systems. The present study revealed that the negative ions produced in the extraction region of the source were locally destructed by fast electrons leaking through magnetic filter. Some countermeasures and their test results are also described.
Sato, Satoshi; Nakao, Makoto*; Verzilov, Y. M.; Ochiai, Kentaro; Wada, Masayuki*; Kubota, Naoyoshi; Kondo, Keitaro; Yamauchi, Michinori*; Nishitani, Takeo
Nuclear Fusion, 45(7), p.656 - 662, 2005/07
Times Cited Count:8 Percentile:27.48(Physics, Fluids & Plasmas)no abstracts in English
Sakamoto, Yoshiteru; Fujita, Takaaki; Ide, Shunsuke; Isayama, Akihiko; Takechi, Manabu; Suzuki, Takahiro; Takenaga, Hidenobu; Oyama, Naoyuki; Kamada, Yutaka; JT-60 Team
Nuclear Fusion, 45(7), p.574 - 580, 2005/07
Times Cited Count:49 Percentile:80.24(Physics, Fluids & Plasmas)This paper reports results on the progress in stationary discharges with a large bootstrap current fraction in JT-60U towards steady-state tokamak operation. In weak shear plasma regime, high-_p ELMy H-mode discharges have been optimized under nearly full non-inductive current drive by the large bootstrap current fraction (fBS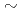 50%) and the beam driven current fraction (fBD
50%) and the beam driven current fraction (fBD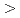 40%), which was sustained for
40%), which was sustained for 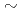 2.3s with stationary condition. The high confinement enhancement factor H89
2.3s with stationary condition. The high confinement enhancement factor H89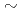 2.3 (HH98y2
2.3 (HH98y2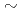 1.0) was also sustained under the condition of Te
1.0) was also sustained under the condition of Te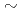 Ti. In reversed shear plasma regime, the large bootstrap current fraction (fBS
Ti. In reversed shear plasma regime, the large bootstrap current fraction (fBS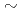 75%) has been sustained for 7.4 s under nearly full non-inductive current drive condition. The high confinement enhancement factor H89
75%) has been sustained for 7.4 s under nearly full non-inductive current drive condition. The high confinement enhancement factor H89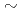 3.0 (HH98y2
3.0 (HH98y2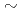 1.7) was also sustained, and the profiles of current and pressure approached the stationary condition. The large bootstrap current and the off-axis beam driven current sustained this reversed q-profile. This duration was limited only by the duration of the neutral beam injection.
1.7) was also sustained, and the profiles of current and pressure approached the stationary condition. The large bootstrap current and the off-axis beam driven current sustained this reversed q-profile. This duration was limited only by the duration of the neutral beam injection.
Nishitani, Takeo; Ochiai, Kentaro; Maekawa, Fujio; Shibata, Keiichi; Wada, Masayuki*; Murata, Isao*
IAEA-CN-116/FT/P1-22 (CD-ROM), 8 Pages, 2004/11
no abstracts in English
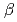 analyses with ferromagnetic and plasma rotation effects and wall geometry for a high
analyses with ferromagnetic and plasma rotation effects and wall geometry for a high 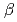 steady state tokamak
steady state tokamakKurita, Genichi; Bialek, J.*; Tsuda, Takashi; Azumi, Masafumi; Ishida, Shinichi; Navratil, G. A.*; Sakurai, Shinji; Tamai, Hiroshi; Matsukawa, Makoto; Ozeki, Takahisa; et al.
IAEA-CN-116/FT/P7-7 (CD-ROM), 8 Pages, 2004/11
The critical beta is shown to be decreased by ferromagnetic effect by about 8 % for m/m0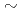 2, m and m0 denote the permeability of ferromagnetic wall and vacuum, respectively, for tokamak of aspect ratio 3. The existence of the stability window opened by both effects of the toroidal plasma rotation and the plasma dissipation, which was not observed for high aspect ratio tokamak, is found for tokamak of aspect ratio 3. The effect of ferromagnetism on them is also investigated. The critical beta analyses of NCT (National Centralized Tokamak) plasma using VALEN code are started with stabilizing plate and vacuum vessel geometry with finite resistivity, and the results for passive effect of stabilizing plate are obtained. The calculations including stabilizing effect of the vacuum-vessel and also active feedback control are also performed for present design of NCT plasma.
2, m and m0 denote the permeability of ferromagnetic wall and vacuum, respectively, for tokamak of aspect ratio 3. The existence of the stability window opened by both effects of the toroidal plasma rotation and the plasma dissipation, which was not observed for high aspect ratio tokamak, is found for tokamak of aspect ratio 3. The effect of ferromagnetism on them is also investigated. The critical beta analyses of NCT (National Centralized Tokamak) plasma using VALEN code are started with stabilizing plate and vacuum vessel geometry with finite resistivity, and the results for passive effect of stabilizing plate are obtained. The calculations including stabilizing effect of the vacuum-vessel and also active feedback control are also performed for present design of NCT plasma.
Miyato, Naoaki; Li, J. Q.*; Kishimoto, Yasuaki
IAEA-CN-116/TH/8-5Rb (CD-ROM), 8 Pages, 2004/11
Using a global Landau fluid code in toroidal geometry, an electromagnetic ion temperature gradient (ITG) driven turbulence-zonal mode system is investigated. Two different types of zonal flows, i.e. stationary zonal flows in a low 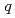 (safety factor) region and oscillatory ones in a high
(safety factor) region and oscillatory ones in a high 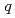 region which are called geodesic acoustic modes (GAM), are found to be simultaneously excited in a torus. The stationary flows efficiently suppress turbulent transport, while the oscillatory ones weakly affect the turbulence due to their time varying nature. Therefore in the low
region which are called geodesic acoustic modes (GAM), are found to be simultaneously excited in a torus. The stationary flows efficiently suppress turbulent transport, while the oscillatory ones weakly affect the turbulence due to their time varying nature. Therefore in the low 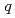 region where the zonal flows are stationary, the zonal flows are dominant over the turbulence. On the other hand, the turbulence is still active in the high
region where the zonal flows are stationary, the zonal flows are dominant over the turbulence. On the other hand, the turbulence is still active in the high 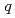 region where the zonal flows are oscillatory.
region where the zonal flows are oscillatory.
Joffrin, E.*; Sips, A. C. C.*; Artaud, J. F.*; Becoulet, A.*; Budny, R.*; Buratti, P.*; Belo, P.*; Challis, C. D.*; Crisanti, F.*; de Baar, M.*; et al.
Proceedings of 20th IAEA Fusion Energy Conference (FEC 2004) (CD-ROM), 8 Pages, 2004/11
no abstracts in English
Hayashi, Nobuhiko; Takizuka, Tomonori; Ozeki, Takahisa
Proceedings of 20th IAEA Fusion Energy Conference (FEC 2004) (CD-ROM), 8 Pages, 2004/11
Profile formation and sustainment of tokamak plasmas with current hole (CH) have been investigated by using 1.5D transport simulations. A current limit model inside CH based on the Axisymmetric Tri-Magnetic-Islands equilibrium is introduced. We found that the sharp reduction of anomalous transport in the reversed-shear (RS) region can reproduce JT-60U experiment. The transport becomes neoclassical-level in RS region, which results in the autonomous formation of internal transport barrier (ITB) and CH through large bootstrap current. ITB width determined by neoclassical-level transport agrees with that in JT-60U. Energy confinement inside ITB agrees with JT-60U scaling, which means autonomous limitation of energy confinement. The plasma with large CH is sustained with the full current drive by bootstrap current. The plasma with small CH and small bootstrap current fraction shrinks due to inductive current penetration. This shrink is prevented and the CH size can be controlled by appropriate external current drive (CD). The CH plasma is found to respond autonomically to external CD.
Konovalov, S. V.; Mikhailovskii, A.*; Ozeki, Takahisa; Takizuka, Tomonori; Shirokov, M. S.*; Hayashi, Nobuhiko
Proceedings of 20th IAEA Fusion Energy Conference (FEC 2004) (CD-ROM), 8 Pages, 2004/11
Influence of anomalous perpendicular heat transport and anomalous perpendicular viscosity on conditions of Neoclassical Tearing Mode onset is studied theoretically. Series of different parallel transport mechanisms competitive to anomalous cross-island heat conductivity in the perturbed temperature profile are considered.In the transport threshold model, magnetic curvature effect is as much important as bootstrap drive weakened by the finite perpendicular heat transport. Perpendicular viscosity brings island-rotation-frequency dependence of the transport threshold model.
Nagasaki, Kazunobu*; Isayama, Akihiko; Hayashi, Nobuhiko; Ozeki, Takahisa; Takechi, Manabu; Oyama, Naoyuki; Ide, Shunsuke; Yamamoto, Satoshi*; JT-60 Team
Proceedings of 20th IAEA Fusion Energy Conference (FEC 2004) (CD-ROM), 8 Pages, 2004/11
no abstracts in English