Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Idomura, Yasuhiro; Ina, Takuya*; Ali, Y.*; Imamura, Toshiyuki*
Proceedings of International Conference for High Performance Computing, Networking, Storage, and Analysis (SC 2020) (Internet), p.1318 - 1330, 2020/11
Times Cited Count:2 Percentile:46.34(Computer Science, Information Systems)The multi-scale full-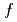 simulation of the next generation experimental fusion reactor ITER based on a five dimensional (5D) gyrokinetic model is one of the most computationally demanding problems in fusion science. In this work, a Gyrokinetic Toroidal 5D Eulerian code (GT5D) is accelerated by a new mixed-precision communication-avoiding (CA) Krylov method. The bottleneck of global collective communication on accelerated computing platforms is resolved using a CA Krylov method. In addition, a new FP16 preconditioner, which is designed using the new support for FP16 SIMD operations on A64FX, reduces both the number of iterations (halo data communication) and the computational cost. The performance of the proposed method for ITER size simulations with 0.1 trillion grids on 1,440 CPUs/GPUs on Fugaku and Summit shows 2.8x and 1.9x speedups respectively from the conventional non-CA Krylov method, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs.
simulation of the next generation experimental fusion reactor ITER based on a five dimensional (5D) gyrokinetic model is one of the most computationally demanding problems in fusion science. In this work, a Gyrokinetic Toroidal 5D Eulerian code (GT5D) is accelerated by a new mixed-precision communication-avoiding (CA) Krylov method. The bottleneck of global collective communication on accelerated computing platforms is resolved using a CA Krylov method. In addition, a new FP16 preconditioner, which is designed using the new support for FP16 SIMD operations on A64FX, reduces both the number of iterations (halo data communication) and the computational cost. The performance of the proposed method for ITER size simulations with 0.1 trillion grids on 1,440 CPUs/GPUs on Fugaku and Summit shows 2.8x and 1.9x speedups respectively from the conventional non-CA Krylov method, and excellent strong scaling is obtained up to 5,760 CPUs/GPUs.
Matsumoto, Kazuya*; Idomura, Yasuhiro; Ina, Takuya*; Mayumi, Akie; Yamada, Susumu
Journal of Supercomputing, 75(12), p.8115 - 8146, 2019/12
Times Cited Count:2 Percentile:20.81(Computer Science, Hardware & Architecture)A communication-avoiding generalized minimum residual method (CA-GMRES) is implemented on a hybrid CPU-GPU cluster, targeted for the performance acceleration of iterative linear system solver in the gyrokinetic toroidal five-dimensional Eulerian code GT5D. In addition to the CA-GMRES, we implement and evaluate a modified variant of CA-GMRES (M-CA-GMRES) proposed in our previous study to reduce the amount of floating-point calculations. This study demonstrates that beneficial features of the CA-GMRES are in its minimum number of collective communications and its highly efficient calculations based on dense matrix-matrix operations. The performance evaluation is conducted on the Reedbush-L GPU cluster, which contains four NVIDIA Tesla P100 GPUs per compute node. The evaluation results show that the M-CA-GMRES is 1.09x, 1.22x and 1.50x faster than the CA-GMRES, the generalized conjugate residual method (GCR), and the GMRES, respectively, when 64 GPUs are used.
Ali, Y.*; Onodera, Naoyuki; Idomura, Yasuhiro; Ina, Takuya*; Imamura, Toshiyuki*
Proceedings of 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2019), p.1 - 8, 2019/11
Times Cited Count:11 Percentile:93.69(Computer Science, Theory & Methods)Iterative methods for solving large linear systems are common parts of computational fluid dynamics (CFD) codes. The Preconditioned Conjugate Gradient (P-CG) method is one of the most widely used iterative methods. However, in the P-CG method, global collective communication is a crucial bottleneck especially on accelerated computing platforms. To resolve this issue, communication avoiding (CA) variants of the P-CG method are becoming increasingly important. In this paper, the P-CG and Preconditioned Chebyshev Basis CA CG (P-CBCG) solvers in the multiphase CFD code JUPITER are ported to the latest V100 GPUs. All GPU kernels are highly optimized to achieve about 90% of the roofline performance, the block Jacobi preconditioner is re-designed to extract high computing power of GPUs, and the remaining bottleneck of halo data communication is avoided by overlapping communication and computation. The overall performance of the P-CG and P-CBCG solvers is determined by the competition between the CA properties of the global collective communication and the halo data communication, indicating an importance of the inter-node interconnect bandwidth per GPU. The developed GPU solvers are accelerated up to 2x compared with the former CPU solvers on KNLs, and excellent strong scaling is achieved up to 7,680 GPUs on the Summit.
Idomura, Yasuhiro; Ina, Takuya*; Yamashita, Susumu; Onodera, Naoyuki; Yamada, Susumu; Imamura, Toshiyuki*
Proceedings of 9th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA 2018) (Internet), p.17 - 24, 2018/11
Times Cited Count:8 Percentile:89.41(Computer Science, Theory & Methods)A communication avoiding (CA) multigrid preconditioned conjugate gradient method (CAMGCG) is applied to the pressure Poisson equation in a multiphase CFD code JUPITER, and its computational performance and convergence property are compared against CA Krylov methods. In the JUPITER code, the CAMGCG solver has robust convergence properties regardless of the problem size, and shows both communication reduction and convergence improvement, leading to higher performance gain than CA Krylov solvers, which achieve only the former. The CAMGCG solver is applied to extreme scale multiphase CFD simulations with 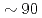 billion DOFs, and it is shown that compared with a preconditioned CG solver, the number of iterations is reduced to
billion DOFs, and it is shown that compared with a preconditioned CG solver, the number of iterations is reduced to 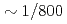 , and
, and 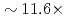 speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
speedup is achieved with keeping excellent strong scaling up to 8,000 nodes on the Oakforest-PACS.
Idomura, Yasuhiro
no journal, ,
The Gyrokinetic Toroidal 5D full-f Eulerian code GT5D is based on a semi-implicit finite difference scheme, in which a stiff linear 4D convection operator is subject to implicit time integration, and the implicit finite difference solver for fast kinetic electrons occupies more than 80% of the total computing cost. The implicit solver was originally developed using a Krylov subspace method, in which global collective communications and halo data communications were becoming bottlenecks on the latest accelerator based platforms. To resolve this issue, the convergence property is improved by using a new FP16 preconditioner, and an order of magnitude reduction of the number of iterations and thus, communications was achieved. A communication-avoiding (CA) solver based on the FP16 preconditioner was developed by utilizing the new support for FP16 SIMD operations on FUGAKU, and was ported also on Summit. The new CA solver showed significant speedups both on FUGAKU and SUMMIT, and its performance portability was demonstrated.
Idomura, Yasuhiro; Ali, Y.*; Onodera, Naoyuki; Hasegawa, Yuta; Ina, Takuya*
no journal, ,
Krylov solvers can account for up to 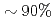 of the total computing cost in extreme scale nuclear CFD simulations. In order to accelerate such CFD codes, we ported the Preconditioned Conjugate Gradient (PCG), Preconditioned Chebyshev Basis communication-avoiding Conjugate Gradient (P-CBCG) and Communication-Avoiding Generalized Minimal RESidual (CA-GMRES) methods on to GPUs. In this talk, we will share our experiences in porting these solvers via OpenACC, CUDA, and CUDA aware MPI.
of the total computing cost in extreme scale nuclear CFD simulations. In order to accelerate such CFD codes, we ported the Preconditioned Conjugate Gradient (PCG), Preconditioned Chebyshev Basis communication-avoiding Conjugate Gradient (P-CBCG) and Communication-Avoiding Generalized Minimal RESidual (CA-GMRES) methods on to GPUs. In this talk, we will share our experiences in porting these solvers via OpenACC, CUDA, and CUDA aware MPI.
Idomura, Yasuhiro
no journal, ,
We discuss Exa-scale computing techniques, which are developed under the Post-K project. Since fusion plasma simulations require first principles based computation of a convection-diffusion simulation in five dimensional phase space, Exa-scale computation is needed for analyzing the next generation experimental reactor ITER. To this end, techniques for utilizing many core processors with low power consumption and avoiding communication bottlenecks, which are revealed by accelerated computation. In this talk, we explain many core optimization techniques, communication-computation overlap techniques, and communication-avoiding algorithms, which have been developed to resolve the above issues, and show their performance evaluations on the latest many core platforms.
Idomura, Yasuhiro; Ali, Y.*; Ina, Takuya*; Imamura, Toshiyuki*
no journal, ,
Implicit finite difference solvers based on Krylov subspace methods occupy dominant computing costs in the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D. Under the post-K project, advanced communication avoiding (CA) Krylov subspace methods have been developed for exascale computing platforms, which have limited inter-node communication performance compared with accelerated computation. In this work, we develop a new mixed precision CA-GMRES solver using a FP16 preconditioner, which dramatically reduces the number of iterations, and thus, halo data communications. We port the new solver on FUGAKU and Summit, and compare its performance against conventional solvers on existing muti/many-core processors.
Ali, Y.*; Onodera, Naoyuki; Idomura, Yasuhiro; Ina, Takuya*; Imamura, Toshiyuki*
no journal, ,
Krylov solvers can account for up to 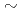 90% of the total computing cost in extreme scale nuclear CFD simulations. In order to accelerate such CFD codes, we ported the conventional Preconditioned Conjugate Gradient (PCG) and the two latest communication avoiding algorithms, the Preconditioned Chebyshev Basis communication-avoiding Conjugate Gradient (P-CBCG) and the Communication-Avoiding Generalized Minimal RESidual (CA-GMRES) methods, on to GPUs. In this talk, we discuss a trade-off between the performance portability and the performance improvement for implementations using OpenACC and CUDA, and show performance tests on the latest GPU supercomputers.
90% of the total computing cost in extreme scale nuclear CFD simulations. In order to accelerate such CFD codes, we ported the conventional Preconditioned Conjugate Gradient (PCG) and the two latest communication avoiding algorithms, the Preconditioned Chebyshev Basis communication-avoiding Conjugate Gradient (P-CBCG) and the Communication-Avoiding Generalized Minimal RESidual (CA-GMRES) methods, on to GPUs. In this talk, we discuss a trade-off between the performance portability and the performance improvement for implementations using OpenACC and CUDA, and show performance tests on the latest GPU supercomputers.
Idomura, Yasuhiro
no journal, ,
Communication-avoiding (CA) algorithms are key technologies towards extreme scale CFD simulations on future exascale machines, which are characterized by accelerated computation and relatively low communication bandwidth. In order to resolve this communication bottleneck, we developed two types of CA-based sparse matrix solvers on extreme scale nuclear simulations such as the five dimensional (5D) fusion plasma turbulence code GT5D and the 3D multi-phase thermal-hydraulic code JUPITER. One is a CA Krylov method, in which multiple basis vectors are generated and orthogonalized at once. By using this approach, one can avoid the bottleneck of All_Reduce communication, which is required at each iteration in the conventional Krylov method. The other is a CA multigrid (MG) method, in which the number of iteration or All_Reduce is reduced by improving the convergence property. In addition, MG implementation with a mixed precision approach reduces both computation and communication. By applying these CA solvers, the performances of GT5D and JUPITER were dramatically improved, and the strong scaling was extended up to the full system size of the Oakforest-PACS, which consists of 8,208 KNLs.
Idomura, Yasuhiro; Ina, Takuya*; Obrejan, K.; Asahi, Yuichi*; Matsuoka, Seikichi*; Imamura, Toshiyuki*
no journal, ,
Under the post-K project, we have developed computing techniques of the Gyrokinetic Toroidal 5D full-f Eulerian code GT5D towards the next generation computing platforms based on many core processors. We discuss computational challenges related to complicated intra-processor memory hierarchy and limited inter-node communication performance compared with accelerated computation. The former issue is addressed by optimizing data access patterns of a stencil kernel on each many core architecture, and high performance gains are obtained. The latter issue is resolved by using advanced communication avoiding Krylov methods, which enables an order of magnitude reduction of collective communications and improves arithmetic intensity of main computing kernels. By applying these novel computing techniques, the performance of GT5D is dramatically improved on the latest many core platforms, and excellent strong scaling up to the full system size of the Oakforest-PACS (8,192 KNLs) is achieved.
Ali, Y.*; Ina, Takuya*; Onodera, Naoyuki; Idomura, Yasuhiro
no journal, ,
Krylov subspace solvers for the pressure Poisson equation occupy 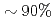 of the total computing cost in extreme scale multi-phase CFD simulation. To accelerate the Poisson solver, we port a Chebyshev Basis communication-avoiding Conjugate Gradient (CBCG) solver with block Jacobi (BJ) preconditioning on P100 GPUs. The CBCG solver consists of BJ preconditioning, Sparse Matrix Vector product (SpMV), and Tall-Skinny matrix operations. We re-design the BJ-preconditioner for thread-block parallelization and efficient coalescing data load, and apply batched gemm to the Tall-Skinny matrix operations. By these optimization, all main kernels achieved
of the total computing cost in extreme scale multi-phase CFD simulation. To accelerate the Poisson solver, we port a Chebyshev Basis communication-avoiding Conjugate Gradient (CBCG) solver with block Jacobi (BJ) preconditioning on P100 GPUs. The CBCG solver consists of BJ preconditioning, Sparse Matrix Vector product (SpMV), and Tall-Skinny matrix operations. We re-design the BJ-preconditioner for thread-block parallelization and efficient coalescing data load, and apply batched gemm to the Tall-Skinny matrix operations. By these optimization, all main kernels achieved 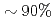 of the theoretical performance based on roofline estimation, and an order of magnitude speedup of the single node performance was obtained against CPU nodes.
of the theoretical performance based on roofline estimation, and an order of magnitude speedup of the single node performance was obtained against CPU nodes.