Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
久語 輝彦; 中川 正幸
Journal of Nuclear Science and Technology, 36(4), p.332 - 343, 1999/04
被引用回数：0 パーセンタイル：0.01(Nuclear Science & Technology)原子炉設計では、設計変数の最適な値を決定するため、多数回のパラメータサーベイ計算を要し、通常、多大な計算時間が費やされる。この作業を支援するため、設計窓、すなわち設計基準や要求仕様を満足する設計変数の範囲を多次元空間において効率的に得る手法を開発し、核及び熱水力設計分野に応用した。本方法の原理は、解析コードにより得られた教師信号を階層型ニューラルネットワークに学習させ、それを解析コードの代わりに用いることによって計算時間の短縮を図るというものである。本手法を高転換型水炉の設計に適用し、ネットワーク構造及び教師データ個数が設計窓の推定精度に与える影響を調べ、本手法の原子炉炉心設計における信頼性及び有効性を評価した。その結果、必要に応じて4層構造を用いて過学習を避ければ、安定的に精度よく設計窓を決定できることを示した。
久語 輝彦; 中川 正幸
Proc. of Int. Conf. on the Phys. of Nucl. Sci. and Technol., 1, p.704 - 711, 1998/00
原子炉炉心設計においては、基本的な設計変数の最適な値を決定するため、通常、多数回のパラメータサーベイ計算を要する。この作業を支援するため、設計窓、すなわち設計基準や要求仕様を満足する設計変数の範囲を多次元空間において効率的に得る手法を開発し、核設計分野に応用した。本方法の原理は、解析コードにより得られた教師信号を階層型ニューラルネットワークに学習させ、それを解析コードの代わりに用いることによって計算時間の短縮を図るというものである。本研究では、ネットワーク構造及び教師データ個数が設計窓の推定精度に与える影響を調査し、本手法の信頼性・有効性を評価した。その高転換型重水炉の設計に適用した結果から、学習パラメータを適切に調整すれば、本手法は安定的に精度よく設計ウィンドウを決定できることを示した。
渡辺 正; 加藤 克海*
画像ラボ, 8(2), p.20 - 22, 1997/02
原研の計算科学研究における可視化技術の利用例として、スーパーコンピュータで実行中のシミュレーションの途中経過を、逐次可視化用ワークステーションへ転送し実時間可視化とビデオ録画、データ保存を行うリアルタイムモニターシステムについて解説した。本システムはスーパーコンピュータ上でのジョブのサブミット用シェル、出力ファイルの転送用シェル、可視化ツールを起動するための描画用シェルからなる。特殊な画像処理技術を使用せずシミュレーションプログラムを変更する必要がないため、様々な計算機環境に応じた使用、拡張が容易である。
後藤 頼男
Journal of Nuclear Science and Technology, 10(10), p.619 - 625, 1973/10
劣化ウラン球体系における高速パルス中性子実験の解析を時間依存多群拡散方程式を用いて行った。時間の短い所での正確な解を求めるために鏡像原理を用いた。逆ラプラス、フーリェ変換は数値的に行った。使った群定数はYOM20群定数とJAERI-FAST70群を20群に縮約したものを用いた。実験と比較した結果、一度も散乱せずに源の中性子が飛んで来るような非常に時間の短かい所をのぞいて拡散方程式で充分記述しうることが明らかになった。この方法をP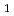
近似に拡張すれば一層良い結果が得られる。
