Solutions of partial differential equations with the CIP-BS method

Utsumi, Takayuki*; Kimura, Hideo

JSME International Journal, Series B, 47(4), p.761 - 767, 2004/11

In this paper, we show that a new numerical method, the Constrained Interpolation Profile - Basis Set (CIP-BS) method, can solve partial differential equations (PDEs) with high accuracy and can be a universal solver by presenting examples for the solutions of typical parabolic, hyperbolic, and elliptic equations. Here, we present the numerical errors caused by this method, and illustrate that the solutions by the CIP-BS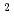 method, in which fifth order polynomials are used to constrain the values and first and second order spatial derivatives, are highly refined compared to those by the CIP-BS 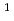method, in which third order polynomials are used to constrain the values and first order spatial derivatives. The fact that this method can unambiguously solve PDEs with an one-to-one correspondence to analytical requirements is also shown for PDEs including singular functions like the Dirac delta function with Dirichet or Neumann boundary conditions. This method is straightforwardly applicable to PDEs describing complex physical and engineering problems.

A Study on various neutron standard fields for workplace

Asano, Yoshihiro

JAERI-Research 99-045, 105 Pages, 1999/08

JAERI-Research-99-045.pdf:3.56MB

no abstracts in English

Nuclear criticality safety handbook, 2

Working Group on Nuclear Criticality Satety Data

JAERI 1340, 189 Pages, 1999/03

JAERI-1340.pdf:8.41MB

no abstracts in English