Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
横田 光史
Physical Review B, 51(2), p.962 - 971, 1995/01
被引用回数：5 パーセンタイル：36.12(Materials Science, Multidisciplinary)ポッツグラス模型(無限レンジ)に対して、秩序相及び1次相転移を調べた。平均場理論の自由エネルギーの収束条件を求めた。ポッツ状態の数が5の時に、平均場方程式系の解を数値的に求めた。ポッツインデックスに対する置換対称性が部分的に回復する解が存在することが見出された。これらの解のレプリカ法による解釈を与えた。1次転移は、パラ相とグラス相の自由エネルギーの大きさの入れ替わりで起きるのではない。レプリカ法で示されている様に、グラス相に対する自由エネルギーは、パラ相の自由エネルギーより常に大きい。イジング模型の場合と異なり、温度の上昇によるグラス解の合流はめったに起きない。
横田 光史
Journal of Physics; Condensed Matter, 4, p.2615 - 2622, 1992/00
被引用回数：11 パーセンタイル：56.65(Physics, Condensed Matter)S=1の結晶場中におけね一般化されたSKイジングスピングラス模型について、スピングラス相と1次相転移を調べた。この模型に対して、平均場方程式を導き、それを数値的に解いた。一次転移線近くでは、P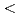i=
Si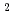
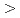のダブルピーク構造が重要であることを示した。この相転移は、定性的にみて、基底状態での相転移に似ている。
