Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
上地 俊*; 上地 宏*; 西村 昭彦
World Journal of Engineering and Technology, 7(4), p.559 - 571, 2019/11
水飲み鳥の動作について熱力学的モデルを論じる。熱力学的モデルから導かれる数学的表現を数値計算の上で明示した。これは機械的な動作と熱力学的な動作の違いに関して基礎的な理解を得ることに助けとなる。機械的な繰り返し動作と熱力学的な繰り返し動作の間には数学的にも物理的にも違いが存在する。この水飲み鳥の工程は本論文で示した手法で環境エネルギー発電に対して適用可能である。
城戸 健太朗
Journal of Computational Chemistry, 40(24), p.2072 - 2085, 2019/09
被引用回数：3 パーセンタイル：10.79(Chemistry, Multidisciplinary)Mean-field treatment of solvent provides an efficient technique to investigate chemical processes in solution in QM/MM framework. In the algorithm, an iterative calculation is required to obtain the self-consistency between QM and MM regions, which is a time-consuming step. In the present study, we have proposed a non-iterative approach by introducing a linear response approximation (LRA) into the solvation term in the one-electron part of Fock matrix in a hybrid approach between MO calculations and a three-dimensional integral equation theory for molecular liquids (MC-MOZ-SCF; Kido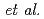 
, J. Chem. Phys. 
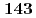, 014103 (2015)). To save the computational time, we have also developed a fast method to generate electrostatic potential map near solute and the solvation term in Fock matrix, using Fourier transformation (FT) and real spherical harmonics expansion (RSHE). To numerically validate the LRA and FT-RSHE method, we applied the present approach to water, carbonic acid and their ionic species in aqueous solution. Molecular properties of the solutes were evaluated by the present approach with four different types of initial wave function and compared with those by the original (MC-MOZ-SCF). From the averaged speed up ratio, the present approach is 13.5 times faster than MC-MOZ-SCF.
永島 芳彦*; 伊藤 公孝*; 伊藤 早苗*; 藤澤 彰英*; 星野 克道; 高瀬 雄一*; 矢木 雅敏*; 江尻 晶*; 居田 克巳*; 篠原 孝司; et al.
Plasma Physics and Controlled Fusion, 48(4), p.S1 - S15, 2006/04
被引用回数：36 パーセンタイル：73.86(Physics, Fluids & Plasmas)JFT-2Mトカマクのオーミック加熱プラズマの浮遊ポテンシャル揺動にバイスぺクトル解析を適用した結果について述べる。最外殻磁気面の内側で浮遊電位揺動中に帯状流の一種と考えられている測地的音波の周波数を持つコヒーレントなモードが観測された。二乗バイコヒーレンスの計算によりそのコヒーレントな揺動と背景揺動(ドリフト波乱流揺動を含むと推定)の間に有意な非線形結合が示された。全バイコヒーレンスは、コヒーレントなモードの振幅の2乗に比例していること、及びコヒーレントなモードは一定値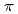
のバイフェイズを持つことなどの測定結果は、長谷川-三間モデルによるドリフト波-帯状流系の理論的予測と整合することがわかった。
市原 潔*; 志澤 由久*; 岸田 則生*
JAERI-Data/Code 99-016, 183 Pages, 1999/03
JAERI-Data-Code-99-016.pdf:4.87MB
「誤差評価ライブラリ」は、行列計算の数値解析結果の誤差の分析を支援するためのサブルーチン集である。(1)連立一次方程式誤差評価ルーチン群は、残差ベクトルのノルム、行列の条件数、誤差限界を計算する。(2)エルミート行列誤差評価ルーチン群は、Korn-Katoの公式に基づいて固有値の存在範囲を見積もる。(3)試験行列生成ルーチン群は、数学研究に基づく試験行列、乱数行列、アプリケーション・プログラムに現れる典型的な行列を生成する。本書は、各サブルーチンが使用している理論・公式の要点と利用方法についてまとめたものである。
岸田 則生*; 加治 芳行; 鈴木 惣一朗*; 清水 大志; 志沢 由久*; 蕪木 英雄
計算工学講演会論文集, 3(1), p.59 - 62, 1998/05
原研で開発中の並列数値計算ライブラリの一つに含まれている安定化双共役勾配法連立一次方程式解法ルーチンを用いて有限要素法プログラムの並列化を行うとともに、高温ガス炉の燃料ブロックの応力解析を行った。有限要素法プログラムの並列化には、連立一次方程式の解法ルーチンを原研開発の解法ルーチンでおきかえる手法を用いた。これはプログラム全体に占める計算時間及び記憶域の大部分が連立方程式解法ルーチンになっているので、ここを並列化することが重要だからである。また、全体を並列化するのに較べて、一部の並列化であっても、その効果が大きいと考えられるからである。実際の応力解析では1200要素から120000要素まで変化させて並列化の効率を調べた。既存プログラムの並列化を行う時、並列ライブラリの使用が極めて有用であることが示せた。
徳田 伸二
プラズマ・核融合学会誌, 74(5), p.503 - 511, 1998/05
回転プラズマにおける線形理想MHD運動を表すフリーマン・ローテンベルグ方程式の双線形形式を導いた。この形式は安定性の解析的及び数値的な研究に適する。この論文では平衡流はトロイダル方向に向いていると仮定する。双線形形式において、反エルミートである対流項を除いて、すべての項はエルミートであることが示される。また、トロイダル流をもつMHD平衡の準中性条件とフリーマン・ローテンベルグ方程式のエルミート性との関係が明らかにされた。
岸田 則生*; 加治 芳行; 清水 大志; 蕪木 英雄
月刊地球, 20(12), p.778 - 782, 1998/00
日本原子力研究所で開発を進めている並列数値計算ライブラリの概要とその応用事例についての紹介を行う。特にライブラリプログラムの一つである双安定化共約勾配法プログラムを用いて有限要素法解析ソフトを並列化した例について、並列性能及び高温工学試験研究炉燃料体ブロックの応力解析結果を記述する。開発したライブラリを科学技術計算プログラムの並列化に利用すると短時間で並列化が終了すること、及び、十分な並列性能を発揮することが確かめられる。
岸田 則生*
RIST News, (26), p.15 - 23, 1998/00
計算科学技術推進センターで開発した並列数値計算ライブラリの紹介を行う。特に連立一次方程式解法プログラムの安定化双共役勾配法ルーチンを有限要素法解析に使用して並列性能を評価した例について詳述する。有限要素法解析には高温工学試験研究炉の燃料体ブロックの応力解析を採用した。疎行列の解法では非ゼロ要素をどのように配列上に格納するかにより、計算性能と並列性能が影響を受ける。そのため、行圧縮格納形式とぎざぎざ対角格納型式を用いた計算をスカラー並列及びベクトル並列計算機上で行って性能を測定した。その結果、一行当りの非ゼロ要素数が大きいと、行圧縮型形式でも十分なベクトル性能が得られることが判明した。
市原 潔*
JAERI-Data/Code 97-011, 25 Pages, 1997/03
JAERI-Data-Code-97-011.pdf:0.8MB
複素数連立一次方程式およびエルミート固有値問題を数値計算によって解いた場合の誤差の分析に必要なデータ取得を支援するサブルーチンを開発した。複素数連立一次方程式については、残差ベクトルのノルム、係数行列の条件数、解の誤差限界を計算する。エルミート行列固有値問題については、Korn-Katoの公式に基づいて、固有値の存在範囲を計算する。上記それぞれについて、逐次計算機用と並列計算機用が用意されている。本報告書は、サブルーチンで使用している精度評価公式の要点と、サブルーチンの利用方法についてまとめたものである。
金野 秀敏*; 林 光二; 篠原 慶邦
Journal of Nuclear Science and Technology, 29(6), p.530 - 546, 1992/06
温度と自動制御からの遅れフィードバックを持つ1成分原子炉動特性(非線形)を研究している。炉出力振動を生起する必要条件は、これら2つの異なった遅れフィードバック間の競合である事が示される。モデルは、炉出力振動の特徴から、付加雑音源を持つ確率ファンデルポール方程式に変換され、これによって非線形相互作用の重要性と外来雑音の効果は質的に理解できる。振動の飽和振幅の推定のための理論的方法もまた、飽和振幅のより精確な理論的予測のために開発した。
大和田 謙
Trends Chem. Phys., 1, p.21 - 30, 1990/00
前報で提案した分子エネルギー成分の近似計算法の理論的背景を明らかにするため、Schroedinger波動方程式を基礎として、2原子分子に対する非同次線形1階、2階、3階および高階微分方程式を導いた。これらの有用な微分方程式を導く過程において、Hellmann-Feynman定理および量子力学的ヴィリアル定理が重要な役割を果たしていることがわかった。微分方程式の一般解の考察から、Qnr(R)=一定の仮定のもとに、平衡位置付近での近似ポテンシャルエネルギー関数を求めることができた。上記の結果は、2原子分子の分子エネルギー成分のみではなく、多原子分子のエネルギー成分も求めることが可能であることを示唆している。
栗田 源一
JAERI-M 82-093, 56 Pages, 1982/07
トカマク・プラズマのMHD的ふるまいが時間依存コードを使って数値的に調べられた。まず理想MHDモードに関して位置不安定性を含んだ外部不安定性の解析を行なった。そのために線形と非線形の理想MHDコードが開発された。線形コードによって外部キンク不安定性に対するトロイダル効果と導体壁の効果が詳しく調べられた。又新しいリゾーニングのアルゴリズムを考案しそれが円筒配位に於て軸対称なプラズマの摂動を数値的に充分良く表現することを示した。次に抵抗MHDモードに関して我々は簡約化された抵抗MHD方程式を使った非線形コードを開発した。そのコードを使って我々は大破壊型不安定性の過程と低n抵抗モードの性質を調べた。そしてトロイダル効果と有限ポロイダルベータの効果が重要であることを見出した。その結果から大破壊型不安定性の初期化に関して新しいシナリオを提案した。
藤村 統一郎
JAERI-M 7553, 28 Pages, 1978/03
科学計算用サブルーチン・ライブラリー(SSL)のベンチマーク・テストに先立ち、連立一次方程式をそれぞれ異なった方法で解くプログラム開発および整備を行った。整備されたプログラムは合同法、乗積型逆行列法、直交化法によるものや反復法を加速するものが主である。一方、開発されたプログラムはエスカレーター法、直接的平行残差法、それに帯形の系を対象とした区画化3重対角法によるもので、それらの使用法が述べられ、改良のための検討が行われている。また、テストのための簡単な例題とプログラム・リストも与えられる。
朝岡 卓見
JAERI-M 7552, 61 Pages, 1978/03
実変数の非線形実関数の連立方程式の1つの解を、推定値から求める数値解法として、準Newtron法と射影法とを概観し、それによる計算プログラムの整備とベンチマーク・テストを実施した。ヤコビアン行列の微分形を与えなくてよいルーチンとしては、PowellのNSO1A、ヤコピアンが疎な系を対象としたReidのNSO3A、及びBrownのNONLINの3つが取り扱われた。これらはいずれも準Newtron法を用いているが、この中ではNONLINが最も安定したアルゴリズムをもっており、計算時間も短くて優れている。ヤコビアンの微分形を与えるルーチンとしては、Boggsのアルゴリズムによる準Newtron法のINTECHと、Georg&Kellerによる射影法のPROJA、及びNSO3Aの1つのオプション、の3つを取り扱った。この結果、射影法はまだ、最適なアルゴリズムを与えるには研究が必要だが、線形変数のみを別個に扱えるINTECHが、この中では一応計算時間の点でも優れていることが示された。
朝岡 卓見
JAERI-M 7335, 88 Pages, 1977/10
科学用サブルーチン・ライブラリの拡充整備の一環として、高次代数方程式の主な数値解法アルゴリズムを概観し、代表的な計算プログラムを整備し、既存のルーチンも含めてベンチマーク・テストを実施した。逆補間法のルーチンとしては、Muller法のプログラムを整備すると共に、これにChambersのアルゴリズムを取り入れたものも作成した。このMuller-Chambers法のルーチンは、3重根3つの近接根などを除けば、特に複素係数多項式の根の計算に有用である。Newton法の変形であるMadsenアルゴリズムによるルーチンも整備したが、低次多項式の根の算出には他より時間がかかるが、すべての場合に正確な解を与えており、標準的な計算プログラムとして用いることができる。実係数多項式に対する既存のBairston法ルーチンは、3重根などを除けば最も速いアルゴリズムになっていることも示された。なお求められた根の誤差限界の計算ルーチンを整備された。
中原 康明; 伊勢 武治; 小林 健介; 伊藤 保之*
JAERI-M 6351, 52 Pages, 1975/12
2次の非線型性を持つ非線型ボルテラ型微積分方程式の新しい数値解法が開発された。変数の領域を部分区間に分割し、この部分区間毎に区間別近似を通用する。まず、部分区間について方程式を積分して、区間別方程式を求め、これに陽近似、陰近似、クランク・ニコルソン法、1次内挿法及び2次と3次のスプライン法の6通りの近似的取扱いを試みた。各時間ステップ毎の数値解は得られた2次代数万程式の正の実魂として直接求められる。我々のアルゴリズムを一点炉動特性に対するアルゴンヌのベンチマーク問題と高速炉のモデル問題に適用した。陰近似は常に安定、3次のスプライン法は発散する、他の方法はこの中間に位するが、安定性、収束性、精度及びCPU時間から評価すると、クランク・ニコルソン法が最も良いとの結論が得られた。さらに、我々のアルゴリズムを非線型核融合炉動特性方程式に適用した。
