Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
井口 正; 浅香 英明; 中村 秀夫
JAERI-Research 2002-006, 152 Pages, 2002/03
JAERI-Research-2002-006.pdf:5.52MB
筆者らは、BWR炉心での核熱水力不安定性の機構を解明するために、THYNC実験を行っている。THYNC実験では、実炉の炉心流動を忠実に模擬すべく、試験部出口にオリフィス抵抗体を、試験部内に丸セル型スペーサを設置している。THYNC実験データの解析には、オリフィス抵抗体やスペーサの流動抵抗を知っておく必要がある。そこで、THYNC試験装置のオリフィス抵抗体及びスペーサの単相流時及び二相流時の流動抵抗を測定した。その結果を用いて、流動抵抗のパラメータ依存性を検討した。併せて、分離流などの基本的な二相流モデルの二相流増倍係数に対する適用性を検討した。その結果、以下のことがわかった。(1)単相流時の流動抵抗は、Re数の関数として、圧力,質量流束の影響を表現できる。また、流動抵抗の予測には、従来の予測法により、流動抵抗を精度よく予測できる。ただし、スペーサについては、流路占有率などの複雑な形状依存性があるため、流動抵抗の高精度の予測には、実験で実験定数を定める必要があった。(2)二相流増倍係数とクオリティの関係は、圧力2MPa~7MPaでは線型関係とみなせる。二相流増倍係数とクオリティの関係は、圧力,形状に依存し、質量流束の影響は小さい。(3)オリフィス及びスペーサの二相流増倍係数は、分離流モデルで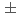
20%の精度で予測できる。適用範囲は、圧力2MPa~7MPa,質量流束133kg/m
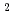s~667kg/m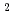sである。一方、均質流モデルでは、実験定数を導入しないと高精度の予測はできない。形状に依存した実験定数を導入することにより、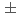20%の精度で予測できる。
中村 秀夫; 安濃田 良成; 久木田 豊
ANS Proc. 1991 National Heat Transfer Conf., Vol. 5, p.269 - 276, 1991/00
ROSA-IV/TPTF装置を用いて、内径180mmまでの大きさの水平管で、圧力3~12MPaでの蒸気/水二相流実験を実施してきた。これまでの実験から、分離流(層状、波状)との間歇流(スラグ、プラグ)間の流動様式遷移条件は、圧力、配管内径などに依存することがわかっている。特に8.9MPaより高い圧力では、スラグ流は観察されていない。ここでは、流動様式遷移条件の配管内径依存性及び、流体密度信号の統計的解析に基づく確率密度関数及びモーメントと流動様式との相関関係について調べた。その結果、流動様式遷移条件の配管内径依存性は、無次元見掛け液流速で良く表現されること、更に、流体密度の統計的解析は、流動様式の判別に有効であることがわかった。
岩村 公道; 黒柳 利之
JAERI-M 9012, 75 Pages, 1980/08
流量低下バーンアウト実験を解析するため、分離流モデルにより沸騰二相流過度挙動の計算を行なって、以下の諸点が明らかとなった。1)流速減少率が2%/sec以下では、出口バーンアウト質量速度計算値G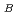
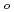
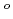
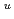
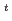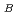
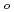
および入口バーンアウト質量速度G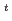は、定常値G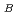
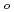
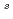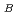
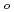
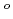
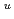
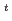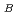
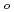
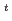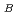
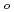
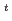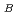
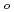
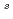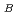
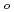
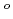
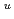
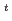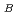
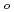
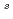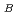
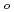
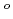
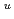
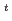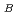
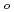
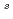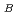
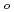
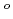
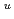
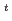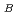
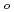
にほぼ一致した。2)流速減少率が大きくなるほど、GとGの差は拡大する。3)圧力が2~3.9MPaの場合、流速減少率が2~20%/secの範囲では、G/Gが約1.0~0.9とやや低下しているにもかかわらず、G/Gはほぼ1となる。また、流速減少率が20%/sec以上ではG/Gは1よりやや大きくなる傾向にある。4)約1MPa以下の圧力では、流速減少率が2%/sec以上になるとG/G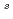は1より小さくなる。