Geometric analysis of phase bunching in the central region of cyclotron
Miyawaki, Nobumasa; Fukuda, Mitsuhiro*; Kurashima, Satoshi; Kashiwagi, Hirotsugu; Okumura, Susumu; Arakawa, Kazuo*; Kamiya, Tomihiro
An optimum condition for realizing phase bunching in the central region of a cyclotron was quantitatively clarified by a simplified geometric trajectory analysis of charged particles from the first to the second acceleration gap. The phase-bunching performance was evaluated for a general case of a cyclotron. The phase difference of incident particles at the second acceleration gap depends on the combination of four parameters: the acceleration harmonic number 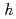 , the span angle
, the span angle 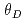 of the dee electrode, the span angle
of the dee electrode, the span angle 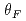 from the first to the second acceleration gap, the ratio
from the first to the second acceleration gap, the ratio 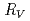 of the peak acceleration voltage between the cyclotron and ion source. Optimum values of
of the peak acceleration voltage between the cyclotron and ion source. Optimum values of 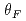 for phase bunching were limited by the relationship between
for phase bunching were limited by the relationship between 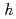 and
and 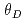 , which is 90
, which is 90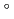 /
/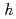 +
+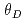 /2
/2 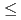
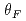
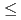 180
180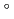 /
/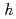 +
+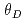 /2, and sin
/2, and sin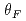
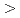 0. The phase difference with respect to the reference particle at the second acceleration gap is minimized for voltage-ratios between two and four for an initial phase difference within 40 RF degrees. Although the slope of the first acceleration gap contributes to the RF phase at which the particles reach the second acceleration gap, phase bunching was not affected. An orbit simulation of the JAEA AVF cyclotron verifies the evaluation based on geometric analysis.
0. The phase difference with respect to the reference particle at the second acceleration gap is minimized for voltage-ratios between two and four for an initial phase difference within 40 RF degrees. Although the slope of the first acceleration gap contributes to the RF phase at which the particles reach the second acceleration gap, phase bunching was not affected. An orbit simulation of the JAEA AVF cyclotron verifies the evaluation based on geometric analysis.