Phase-field model for crystallization in alkali disilicate glasses; LiO-2SiO, NaO-2SiO and KO-2SiO

二酸化アルカリケイ酸ガラスにおける結晶化のフェーズフィールドモデル; LiO-2SiO, NaO-2SiO及びKO-2SiO

河口 宗道   ; 宇埜 正美*

Kawaguchi, Munemichi; Uno, Masayoshi*

本研究では、移動度係数(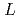)を新しく定義することで、溶融酸化物系におけるフェーズフィールド法(PFM)の技術を開発した。一定の移動係数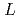を用いたPFM計算から得られた結晶成長速度(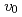)は、normal growthモデルの熱力学的推進力と同程度であった。また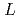の温度依存性は、実験から得られた結晶成長速度と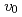から決定し、その決定した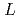を使って、二酸化アルカリケイ酸ガラスのLiO-2SiO, NaO-2SiO, KO-2SiOの結晶成長速度(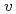)をシミュレーションした。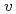の温度依存性は定性的および定量的に非常に良く一致したため、本PFM計算は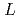の有効性を実証した。特に、PFM計算によって得られた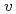は、融点(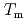)で増大し、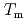-100Kでピークを示した。さらなる温度の下降では、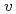は明確に0ms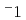に近づくことが分かった。この振舞いは、界面のジャンプ過程を表現する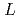によって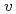が制限されているためである。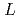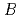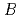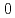のパラメータの感度についてもPFM計算を行い、がから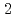まで増加すると、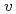のピークはより急峻に、ピーク温度は高温側にシフトすることが分かった。アルカリ金属の原子番号が増加するにつれてイオンポテンシャルは減少するので、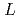のパラメータ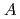と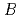は、それぞれ指数関数的に増加、直線的に減少することになったと考えられる。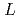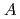本計算によりのと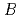は互いに密接な関係であることが分かった。

This study developed phase-field method (PFM) technique in oxide melt system by using a new mobility coefficient (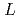). The crystal growth rates (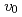) obtained by the PFM calculation with the constant 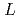were comparable to the thermodynamic driving force in normal growth model. The temperature dependence of the 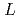was determined from the experimental crystal growth rates and the 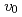. Using the determined 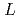, the crystal growth rates (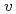) in alkali disilicate glasses, LiO-2SiO, NaO-2SiO and KO-2SiO were simulated. The temperature dependence of the 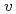was qualitatively and quantitatively so similar that the PFM calculation results demonstrated the validity of the 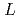. Especially, the 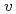obtained by the PFM calculation appeared the rapid increase just below the thermodynamic melting point (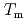) and the steep peak at around 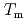-100 K. Additionally, as the temperature decreased, the 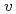apparently approached zero ms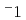, which is limited by the 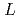representing the interface jump process. Furthermore, we implemented the PFM calculation for the variation of the parameter 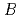in the 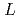. As the 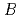increased from zero to two, the peak of the 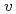became steeper and the peak temperature of the 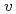shifted to the high temperature side. The parameters 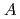and 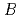in the 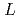increased exponentially and decreased linearly as the atomic number of the alkali metal increased due to the ionic potential, respectively. This calculation revealed that the 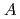and 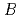in the 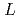were close and reasonable for each other.