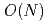Incompleteness of the large- analysis of the models; Nonperturbative cuspy fixed points and their nontrivial homotopy at finite

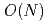模型のLarge-解析の不完全性; 非摂動的なカスプを有する固定点と有限のでの非自明なホモトピー

藪中 俊介; Fleming, C.*; Delamotte, B.*

Yabunaka, Shunsuke; Fleming, C.*; Delamotte, B.*

We summarize the usual implementations of the large- limit of 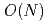models and show in detail why and how they can miss some physically important fixed points when they become singular in the infinite . Using Wilson's renormalization group in its functional nonperturbative versions, we show how the singularities build up as increases. In the Wilson-Polchinski version of the nonperturbative renormalization group, we show that the singularities are cusps, which become boundary layers for finite but large values of . The corresponding fixed points being never close to the Gaussian, are out of reach of the usual perturbative approaches. We find four new fixed points and study them in all dimensions and for all and show that they play an important role for the tricritical physics of 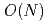models. Finally, we show that some of these fixed points are bi-valued when they are considered as functions of 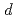and thus revealing important and nontrivial homotopy structures.