Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
藪中 俊介; Delamotte, B.*
Journal of Statistical Mechanics; Theory and Experiment, 2025, p.023204_1 - 023204_22, 2025/02
We revisit the critical behavior of classical frustrated systems using the nonperturbative renormalization group (NPRG) equation. Our study is performed within the local potential approximation of this equation to which is added the flow of the field renormalization. Our flow equations are functional to avoid possible artifacts coming from the field expansion of the fixed point potential which consists in keeping only a limited number of coupling constants. We explain in detail our numerical implementation, its advantages and the difficulties encountered in the vicinity of 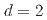 . For N-component spins, the function
. For N-component spins, the function 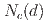 separating the regions of first and second order transitions in the
separating the regions of first and second order transitions in the 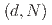 plane is computed for d between 4 and 2.3. Our results confirm what was previously found with cruder approximations of the NPRG equation and contradict both the fixed dimension perturbative approach and some of the results obtained within the conformal bootstrap approach.
plane is computed for d between 4 and 2.3. Our results confirm what was previously found with cruder approximations of the NPRG equation and contradict both the fixed dimension perturbative approach and some of the results obtained within the conformal bootstrap approach.
 ) models at large
) models at large 
藪中 俊介; Delamotte, B.*
Physical Review Letters, 130(26), p.261602_1 - 261602_6, 2023/06
被引用回数:1 パーセンタイル:22.15(Physics, Multidisciplinary)We show that at 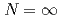 and below its upper critical dimension,
and below its upper critical dimension, 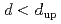 , the critical and tetracritical behaviors of the O
, the critical and tetracritical behaviors of the O models are associated with the same renormalization group fixed point (FP) potential. Only their derivatives make them different with the subtleties that taking their
models are associated with the same renormalization group fixed point (FP) potential. Only their derivatives make them different with the subtleties that taking their 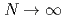 limit and deriving them do not commute and that two relevant eigenperturbations show singularities. This invalidates both the
limit and deriving them do not commute and that two relevant eigenperturbations show singularities. This invalidates both the 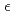 - and the
- and the 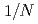 - expansions. We also show how the Bardeen-Moshe-Bander line of tetracritical FPs at
- expansions. We also show how the Bardeen-Moshe-Bander line of tetracritical FPs at 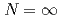 and
and 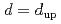 can be understood from a finite-
can be understood from a finite- analysis.
analysis.
 analysis of the
analysis of the 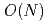 models; Nonperturbative cuspy fixed points and their nontrivial homotopy at finite
models; Nonperturbative cuspy fixed points and their nontrivial homotopy at finite 
藪中 俊介; Fleming, C.*; Delamotte, B.*
Physical Review E, 106(5), p.054105_1 - 054105_29, 2022/11
被引用回数:5 パーセンタイル:58.27(Physics, Fluids & Plasmas)We summarize the usual implementations of the large- limit of
limit of 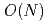 models and show in detail why and how they can miss some physically important fixed points when they become singular in the infinite
models and show in detail why and how they can miss some physically important fixed points when they become singular in the infinite  . Using Wilson's renormalization group in its functional nonperturbative versions, we show how the singularities build up as
. Using Wilson's renormalization group in its functional nonperturbative versions, we show how the singularities build up as  increases. In the Wilson-Polchinski version of the nonperturbative renormalization group, we show that the singularities are cusps, which become boundary layers for finite but large values of
increases. In the Wilson-Polchinski version of the nonperturbative renormalization group, we show that the singularities are cusps, which become boundary layers for finite but large values of  . The corresponding fixed points being never close to the Gaussian, are out of reach of the usual perturbative approaches. We find four new fixed points and study them in all dimensions and for all
. The corresponding fixed points being never close to the Gaussian, are out of reach of the usual perturbative approaches. We find four new fixed points and study them in all dimensions and for all  and show that they play an important role for the tricritical physics of
and show that they play an important role for the tricritical physics of 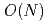 models. Finally, we show that some of these fixed points are bi-valued when they are considered as functions of
models. Finally, we show that some of these fixed points are bi-valued when they are considered as functions of 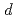 and
and  thus revealing important and nontrivial homotopy structures.
thus revealing important and nontrivial homotopy structures.
藪中 俊介; Fleming, C.*; Delamotte, B.*
no journal, ,
We summarize the usual implementations of the large N limit of O(N) models and show in detail why and how they can miss some physically important fixed points when they become singular in the infinite N. Using Wilson's renormalization group in its functional nonperturbative versions, we show how the singularities build up as N increases. In the Wilson-Polchinski version of the nonperturbative renormalization group, we show that the singularities are cusps, which become boundary layers for finite but large values of N. The corresponding fixed points being never close to the Gaussian, are out of reach of the usual perturbative approaches. We find four new fixed points and study them in all dimensions and for all N and show that they play an important role for the tricritical physics of O(N) models. Finally, we show that some of these fixed points are bi-valued when they are considered as functions of d and N thus revealing important and nontrivial homotopy structures.
藪中 俊介; Delamotte, B.*
no journal, ,
We show that at 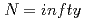 and below its upper critical dimension,
and below its upper critical dimension, 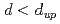 , the critical and tetracritical behaviors of the
, the critical and tetracritical behaviors of the 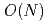 models are associated with the same renormalization group fixed point (FP) potential. Only their derivatives make them different with the subtleties that taking their
models are associated with the same renormalization group fixed point (FP) potential. Only their derivatives make them different with the subtleties that taking their 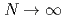 limit and deriving them do not commute and that two relevant eigenperturbations show singularities. This invalidates both the
limit and deriving them do not commute and that two relevant eigenperturbations show singularities. This invalidates both the 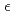 - and the
- and the 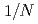 - expansions. We also show how the Bardeen-Moshe-Bander line of tetracritical FPs at
- expansions. We also show how the Bardeen-Moshe-Bander line of tetracritical FPs at 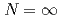 and
and 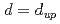 can be understood from a finite-
can be understood from a finite- analysis.
analysis.
藪中 俊介; Delamotte, B.*
no journal, ,
We find that the multicritical fixed point structure of the O( ) models is much more complicated than widely believed. In particular, we find new nonperturbative fixed points in three dimensions (
) models is much more complicated than widely believed. In particular, we find new nonperturbative fixed points in three dimensions (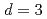 ) as well as at
) as well as at 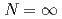 and for
and for 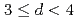 . These fixed points come together with an intricate homotopy structure when they are considered as functions of
. These fixed points come together with an intricate homotopy structure when they are considered as functions of 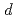 and
and 
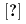 . The fact that the new nonperturbative fixed points at
. The fact that the new nonperturbative fixed points at 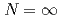 had not been found questions the conventional large
had not been found questions the conventional large  expansion, which plays a fundamental role in quantum and statistical field theory. We show on the example of the O
expansion, which plays a fundamental role in quantum and statistical field theory. We show on the example of the O model that at
model that at 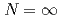 , its standard implementation misses in all dimensions below
, its standard implementation misses in all dimensions below 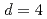 the new nonperturbative fixed points. These new fixed points show singularities under the form of cusps at
the new nonperturbative fixed points. These new fixed points show singularities under the form of cusps at 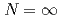 in their effective potential that become a boundary layer at finite
in their effective potential that become a boundary layer at finite  . We show that they have a physical impact on the multicritical physics of the
. We show that they have a physical impact on the multicritical physics of the 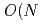 ) model at finite
) model at finite  . We also show that the boundary layer also plays a role for the tetracritical case
. We also show that the boundary layer also plays a role for the tetracritical case  , but in a different way than the tricritical case.
, but in a different way than the tricritical case.