Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
池田 義雅*; 竹谷 篤*; 高村 正人*; 須長 秀行*; 熊谷 正芳*; 大場 洋次郎*; 大竹 淑恵*; 鈴木 裕士
Nuclear Instruments and Methods in Physics Research A, 833, p.61 - 67, 2016/10
被引用回数:41 パーセンタイル:96.16(Instruments & Instrumentation)小型中性子源を利用した透過イメージングや小角散乱、反射率測定など、小型中性子源による工学的応用に関する議論が広まるなか、小型中性子源のフラックスの低いゆえに回折実験に関する検討はなされてこなかった。そこで本研究では、理化学研究所の小型加速器中性子源RANSを用いることにより、中性子工学回折実験への応用の可能性について検討した。まず、光学系の最適化によるバックグラウンドノイズの低減により、10分間の測定でも十分に認識可能な回折パターンを得ることができた。110回折のプロファイルから計算した分解能は約2.5%であり、中性子回折によるひずみ測定には不十分である。RANSのモデレータによる減速時間が約30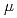 sと分解能の決定に最も支配的なパラメータであることから、モデレータの改良が分解能の向上につながる。一方で、回折パターンの変化から、塑性変形に伴う集合組織の変化をとらえることに成功するとともに、リートベルトコードによる回折パターンのフィッティングにより、オーステナイト相の体積率の評価にも成功した。RANSは、集合組織や残留オーステナイト量の測定を目的とした中性子工学回折の応用に有効と考えられる。
sと分解能の決定に最も支配的なパラメータであることから、モデレータの改良が分解能の向上につながる。一方で、回折パターンの変化から、塑性変形に伴う集合組織の変化をとらえることに成功するとともに、リートベルトコードによる回折パターンのフィッティングにより、オーステナイト相の体積率の評価にも成功した。RANSは、集合組織や残留オーステナイト量の測定を目的とした中性子工学回折の応用に有効と考えられる。
高村 正人*; 池田 義雅*; 須長 秀行*; 竹谷 篤*; 大竹 淑恵*; 鈴木 裕士; 熊谷 正芳*; 浜 孝之*; 大場 洋次郎*
Journal of Physics; Conference Series, 734(Part B), p.032047_1 - 032047_4, 2016/08
被引用回数:5 パーセンタイル:84.66(Physics, Applied)中性子回折法は、中性子線の優れた透過能を活かすことで、金属材料のバルク集合組織を測定できる技術として知られている。しかしながら、この測定技術は、原子炉や加速器施設などの大型実験施設を必要とするため、あまり広く利用されていないのが現状である。一方、理研小型中性子源(RANS)は、実験室レベルで容易に利用できる中性子源として開発されている。本研究では、RANSを用いることにより、塑性変形した鋼板の集合組織の変化を捉えることに成功した。本結果は、金属材料のミクロ組織解析に対する小型中性子源の可能性を示すものであり、塑性変形挙動のより良い理解につながるものと期待される。
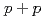 collisions at
collisions at 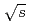 = 200 GeV
= 200 GeVAdare, A.*; Afanasiev, S.*; Aidala, C.*; Ajitanand, N. N.*; Akiba, Y.*; Al-Bataineh, H.*; Alexander, J.*; Aoki, K.*; Aphecetche, L.*; Armendariz, R.*; et al.
Physical Review D, 84(1), p.012006_1 - 012006_18, 2011/07
被引用回数:33 パーセンタイル:75.28(Astronomy & Astrophysics)重心エネルギー200GeVでの縦偏極陽子陽子衝突からのジェット生成のイベント構造と二重非対称(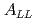 )について報告する。光子と荷電粒子がPHENIX実験で測定され、イベント構造がPHYTIAイベント生成コードの結果と比較された。再構成されたジェットの生成率は2次までの摂動QCDの計算で十分再現される。測定された
)について報告する。光子と荷電粒子がPHENIX実験で測定され、イベント構造がPHYTIAイベント生成コードの結果と比較された。再構成されたジェットの生成率は2次までの摂動QCDの計算で十分再現される。測定された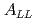 は、一番低い横運動量で-0.0014
は、一番低い横運動量で-0.0014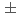 0.0037、一番高い横運動量で-0.0181
0.0037、一番高い横運動量で-0.0181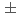 0.0282であった。この
0.0282であった。この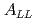 の結果を幾つかの
の結果を幾つかの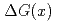 の分布を仮定した理論予想と比較する。
の分布を仮定した理論予想と比較する。
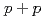 collisions at
collisions at 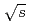 = 200 and 62.4 GeV
= 200 and 62.4 GeVAdare, A.*; Afanasiev, S.*; Aidala, C.*; Ajitanand, N. N.*; 秋葉 康之*; Al-Bataineh, H.*; Alexander, J.*; 青木 和也*; Aphecetche, L.*; Armendariz, R.*; et al.
Physical Review C, 83(6), p.064903_1 - 064903_29, 2011/06
被引用回数:192 パーセンタイル:99.39(Physics, Nuclear)200GeVと62.4GeVでの陽子陽子の中心衝突からの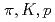 の横運動量分布及び収量をRHICのPHENIX実験によって測定した。それぞれエネルギーでの逆スロープパラメーター、平均横運動量及び単位rapidityあたりの収量を求め、異なるエネルギーでの他の測定結果と比較する。また
の横運動量分布及び収量をRHICのPHENIX実験によって測定した。それぞれエネルギーでの逆スロープパラメーター、平均横運動量及び単位rapidityあたりの収量を求め、異なるエネルギーでの他の測定結果と比較する。また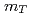 や
や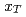 スケーリングのようなスケーリングについて示して陽子陽子衝突における粒子生成メカニズムについて議論する。さらに測定したスペクトルを二次の摂動QCDの計算と比較する。
スケーリングのようなスケーリングについて示して陽子陽子衝突における粒子生成メカニズムについて議論する。さらに測定したスペクトルを二次の摂動QCDの計算と比較する。
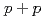 and Au+Au collisions at
and Au+Au collisions at 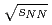 = 200 GeV
= 200 GeVAdare, A.*; Afanasiev, S.*; Aidala, C.*; Ajitanand, N. N.*; 秋葉 康之*; Al-Bataineh, H.*; Alexander, J.*; 青木 和也*; Aphecetche, L.*; Aramaki, Y.*; et al.
Physical Review C, 83(4), p.044912_1 - 044912_16, 2011/04
被引用回数:10 パーセンタイル:54.72(Physics, Nuclear)重いフレーバーのメソンの崩壊からの電子の測定は、このメソンの収量が金金衝突では陽子陽子に比べて抑制されていることを示している。われわれはこの研究をさらに進めて二つの粒子の相関、つまり重いフレーバーメソンの崩壊からの電子と、もう一つの重いフレーバーメソンあるいはジェットの破片からの荷電ハドロン、の相関を調べた。この測定は重いクォークとクォークグルオン物質の相互作用についてのより詳しい情報を与えるものである。われわれは特に金金衝突では陽子陽子に比べて反対側のジェットの形と収量が変化していることを見いだした。
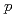 +
+ 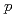 collisions at
collisions at 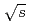 = 200 GeV and scaling properties of hadron production
= 200 GeV and scaling properties of hadron productionAdare, A.*; Afanasiev, S.*; Aidala, C.*; Ajitanand, N. N.*; Akiba, Y.*; Al-Bataineh, H.*; Alexander, J.*; Aoki, K.*; Aphecetche, L.*; Armendariz, R.*; et al.
Physical Review D, 83(5), p.052004_1 - 052004_26, 2011/03
被引用回数:181 パーセンタイル:98.31(Astronomy & Astrophysics)RHIC-PHENIX実験で重心エネルギー200GeVの陽子陽子衝突からの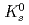 ,
, 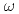 ,
, 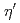 と
と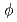 中間子生成の微分断面積を測定した。これらハドロンの横運動量分布のスペクトルの形はたった二つのパラメーター、
中間子生成の微分断面積を測定した。これらハドロンの横運動量分布のスペクトルの形はたった二つのパラメーター、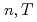 、のTsallis分布関数でよく記述できる。これらのパラメーターはそれぞれ高い横運動量と低い横運動量の領域のスペクトルを決めている。これらの分布をフィットして得られた積分された不変断面積はこれまで測定されたデータ及び統計モデルの予言と一致している。
、のTsallis分布関数でよく記述できる。これらのパラメーターはそれぞれ高い横運動量と低い横運動量の領域のスペクトルを決めている。これらの分布をフィットして得られた積分された不変断面積はこれまで測定されたデータ及び統計モデルの予言と一致している。