Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
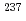 Np and
Np and 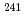 Am by accelerator-driven system at Kyoto University Critical Assembly
Am by accelerator-driven system at Kyoto University Critical AssemblyPyeon, C. H.*; 山中 正朗*; 大泉 昭人; 福島 昌宏; 千葉 豪*; 渡辺 賢一*; 遠藤 知弘*; Van Rooijen, W. G.*; 橋本 憲吾*; 左近 敦士*; et al.
Journal of Nuclear Science and Technology, 56(8), p.684 - 689, 2019/08
被引用回数:12 パーセンタイル:73.30(Nuclear Science & Technology)本研究では、京都大学臨界集合体(KUCA)で構築した未臨界炉心への高エネルギー中性子の入射による加速器駆動システム(ADS)において、マイナーアクチノイド(MA)の核変換の原理が初めて実証された。本実験は、ネプツニウム237(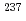 Np)とアメリシウム241(
Np)とアメリシウム241(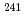 Am)の核分裂反応と、
Am)の核分裂反応と、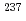 Npの捕獲反応を確認することを主たる目的とした。
Npの捕獲反応を確認することを主たる目的とした。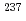 Npおよび
Npおよび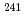 Amの箔の未臨界照射は、試料(
Amの箔の未臨界照射は、試料(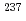 Npまたは
Npまたは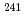 Am)と参照として用いるウラン-235(
Am)と参照として用いるウラン-235(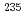 U)のそれぞれの箔からの信号を同時測定可能なback-to-back核分裂計数管を使用し、中性子スペクトルが硬い炉心で行われた。核分裂と捕獲反応の実験結果を通じて、未臨界炉心と100MeVの陽子加速器を組み合わせ、かつ鉛-ビスマスのターゲットを使用したADSによる
U)のそれぞれの箔からの信号を同時測定可能なback-to-back核分裂計数管を使用し、中性子スペクトルが硬い炉心で行われた。核分裂と捕獲反応の実験結果を通じて、未臨界炉心と100MeVの陽子加速器を組み合わせ、かつ鉛-ビスマスのターゲットを使用したADSによる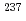 Npと
Npと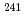 Amの初の核変換が示された。
Amの初の核変換が示された。
Truchet, G.*; Van Rooijen, W. F. G.*; 島津 洋一郎*; 山口 勝久
Annals of Nuclear Energy, 51, p.94 - 106, 2013/01
被引用回数:7 パーセンタイル:46.57(Nuclear Science & Technology)修正中性子増倍法(MNSM)を高速原型炉「もんじゅ」に適用した。「もんじゅ」の特異性のうちMNSM因子に大きな影響を及ぼす要素は、炉心近傍にカリフォルニウム中性子源があることと、中性子検出器が炉容器外の離れた位置にあること。検出器の計数率の評価では、炉容器から外部の検出器までの伝播計算を実施した。二つの未臨界状態に対して反応度を評価し、2010年の再起動試験データと比較した。MNSM法による反応度計算結果は、他の方法から得られた反応度とよい一致を見た。
Van Rooijen, W. F. G.*; 千葉 豪
Annals of Nuclear Energy, 38(1), p.133 - 144, 2011/01
被引用回数:16 パーセンタイル:71.97(Nuclear Science & Technology)高速炉の六角燃料セルについて、ナトリウムがある場合とボイド化した場合の拡散係数の新しい計算モデルを提案する。従来の方法とは異なり、新しいモデルでは平面ボイド領域が存在する体系であっても拡散係数を計算することができる。新しいモデルにより導出される中性子輸送方程式は特性曲線法により解く。このモデルの妥当性を確認するため、モンテカルロ法に基づいて計算した拡散係数との比較を行い、従来の方法では計算できない場合も含むすべての条件で両者がよく一致することを確認した。
Van Rooijen, W. F. G.*; 羽様 平; 竹田 敏一*
Proceedings of Joint International Conference of 7th Supercomputing in Nuclear Application and 3rd Monte Carlo (SNA + MC 2010) (USB Flash Drive), 14 Pages, 2010/10
炉心解析で使用する拡散係数は、現状ではBenoistの手法に基づき、異方性を考慮した衝突確率を用いて求めている。しかしながら、Benoistの手法では、スラブ形状の2次元のボイド領域を含む体系の拡散係数を適切に評価できない。また、ゼロバックリングを仮定しているため、その妥当性も課題である。現在、ボイド領域を含む体系でも適切な拡散係数が得られるように決定論手法による格子計算の改良を図っており、その比較参照に供するためモンテカルロ手法による拡散係数の算出を試みた。
此村 守; Tamagno, P.*; 竹田 敏一*; Van Rooijen, W. F. G.*
no journal, ,
The presentation deals with uncertainty analysis on Monju fast reactor using the JENDL-4.0 nuclear data set and the ERANOS code. For this study, cross-sections library had to be produced for the ERANOS cell code ECCO and verified with the benchmarks MZA and MZB. Monju 2010 restart reactivity measurement was modeled using several libraries. Uncertainty analysis is performed and comparison is done with the former JENDL-3.3 evaluation.
山口 勝久; Truchet, G.*; Van Rooijen, W. F. G.*; 島津 洋一郎*
no journal, ,
The Modified Neutron Multiplication Method (MNMM) which has been applied to LWR was used to determine the reactivity of FRB Monju. Based on publicly available data, a model was made of the Monju reactor during the restart in May 2010. A model of the core and surrounding vollumes was made with the ERANOS software, in which the reactivity states were modeled and the MNMM correction factors were calculated. The reactivity calculated with the MNMM is slightly different from the measured values, but still within the error margins of the measurement.
此村 守; Tamagno, P.*; Van Rooijen, W. F. G.*; 竹田 敏一*
no journal, ,
This paper deals with uncertainty analysis of the Monju reactor using JENDL-4.0 and the ERANOS code. A JENDL-4.0 cross-sections library was made from the original ENDF files for the ECCO cell code (part of ERANOS). Calculations for the Monju reactor were performed using hexagonal 3D geometry and PN transport theory. The corresponding geometrical models have been made and the results verified with Monju restart experimental data. Uncertainty analysis was performed using the RZ model.JENDL-4.0 uncertainty analysis showed a significant reduction of the uncertainty related to the fission cross-section of 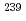 Pu along with an increase of the uncertainty related to the capture cross-section of
Pu along with an increase of the uncertainty related to the capture cross-section of 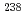 U compared with the previous JENDL-3.3 version. Covariance data recently added in JENDL-4.0 for
U compared with the previous JENDL-3.3 version. Covariance data recently added in JENDL-4.0 for 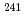 Am appears to have a non negligible contribution.
Am appears to have a non negligible contribution.
千葉 豪; Van Rooijen, W. F. G.*
no journal, ,
非対称単位格子で構成される格子の特性について検討した。方向依存の均質全断面積を導入することにより、単位格子が非対称の場合であっても、通常の単位格子での均質化に基づく従来の決定論的手法により参照解をよく再現する解を得られることを示した。
千葉 豪; Van Rooijen, W. F. G.*
no journal, ,
ボイド領域を含む六角配列の単位格子について異方性拡散係数を計算した。このような計算は、格子計算に通常用いる衝突確率法では困難であるが、特性曲線法を利用することで実現可能となった。本手法により、漏洩理論に基づく忠実な拡散係数を計算することが可能となった。