Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Aiba, Nobuyuki; Hirota, Makoto*
Physics of Plasmas, 22(8), p.082512_1 - 082512_9, 2015/08
Times Cited Count：2 Percentile：9.03(Physics, Fluids & Plasmas)A mechanism exciting magnetohydrodynamic (MHD) instabilities in rotating tokamak plasmas is found numerically for the first time. This mechanism is the interplay between a resistive wall mode (RWM) and a stable MHD mode. When the plasma has a stable discrete eigenmode, a reversed shear Alfv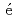
n eigenmode (RSAE) for example, a MHD mode is destabilized when plasma equilibrium rotation frequency is similar to the frequency of this stable eigenmode in a static equilibrium. This destabilization is also observed even when the eigenmode couples with Alfv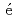n continua. This result suggests that for steady state high beta tokamaks, like DEMO, it is necessary to shape the safety factor profile in such a way that no stable eigenmode exists in the band of rotation frequency. With a dispersion relation, it was shown explicitly that plasma rotation switches the unstable mode from the RWM to the ideal MHD mode destabilized by wall resistivity.
Aiba, Nobuyuki; Hirota, Makoto*
Physical Review Letters, 114(6), p.065001_1 - 065001_5, 2015/02
Times Cited Count：2 Percentile：20.46(Physics, Multidisciplinary)A mechanism exciting magnetohydrodynamic (MHD) instabilities in rotating tokamak plasmas is found numerically for the first time. This mechanism is the interplay between a resistive wall mode (RWM) and a stable MHD mode. When the plasma has a stable discrete eigenmode, a reversed shear Alfv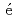n eigenmode (RSAE) for example, a MHD mode is destabilized when plasma equilibrium rotation frequency is similar to the frequency of this stable eigenmode in a static equilibrium. This destabilization is also observed even when the eigenmode couples with Alfv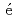n continua. This result suggests that for steady state high beta tokamaks, like DEMO, it is necessary to shape the safety factor profile in such a way that no stable eigenmode exists in the band of rotation frequency.
Aiba, Nobuyuki; Hirota, Makoto*; Matsuyama, Akinobu; Shiraishi, Junya; Bierwage, A.
Proceedings of 25th IAEA Fusion Energy Conference (FEC 2014) (CD-ROM), 8 Pages, 2014/10
A mechanism exciting magnetohydrodynamic (MHD) instabilities in rotating tokamak plasmas is found numerically for the first time. This mechanism is the interplay between a resistive wall mode (RWM) and a stable MHD mode. When the plasma has a stable discrete eigenmode, a reversed shear Alfv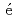n eigenmode (RSAE) for example, a MHD mode is destabilized when plasma equilibrium rotation frequency is similar to the frequency of this stable eigenmode in a static equilibrium. This destabilization is also observed even when the eigenmode couples with Alfv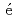n continua. This result suggests that for steady state high beta tokamaks, like DEMO, it is necessary to shape the safety factor profile in such a way that no stable eigenmode exists in the band of rotation frequency.
Hirota, Makoto; Morrison, P. J.*; Ishii, Yasutomo; Yagi, Masatoshi; Aiba, Nobuyuki
Nuclear Fusion, 53(6), p.063024_1 - 063024_11, 2013/06
Times Cited Count：9 Percentile：37.34(Physics, Fluids & Plasmas)A mechanism for fast magnetic reconnection in collisionless plasma is studied for understanding sawtooth collapse in tokamak discharges. Explosive growth of the tearing mode driven by electron inertia is analytically estimated by using an energy principle with a nonlinear displacement map. Decrease of the potential energy in the nonlinear regime (where the island width exceeds the electron skin depth) is found to be steeper than in the linear regime, resulting in accelerated reconnection. Release of free energy by such ideal fluid motion leads to unsteady and strong convective flow, which is not deterred by the small dissipation effects in high-temperature tokamak plasmas. Direct numerical simulation in slab geometry substantiates the theoretical prediction of the nonlinear growth.
Aiba, Nobuyuki; Shiraishi, Junya; Hirota, Makoto
Plasma Physics and Controlled Fusion, 55(7), p.074002_1 - 074002_7, 2013/00
Times Cited Count：6 Percentile：26.2(Physics, Fluids & Plasmas)The authors identified that plasma poloidal rotation sometimes plays an important role for ideal MHD stability due to changing the Doppler-shift frequency. As the result, the stability of edge localized MHD mode can depends on the direction of toroidal rotation; this dependence is qualitatively consistent with the experimental results observed in JT-60U. Plasma rotation is also responsible for the stability of resistive wall mode (RWM). In reversed shear plasmas, plasma rotation once stabilize this RWM but destabilize this again when rotation frequency reaches to certain frequency. This re-destabilization is thought to be related to the coupling between RWM and a stable MHD wave; this coupling is one of the destabilizing mechanisms discussed in previous theoretical papers. This re-destabilized RWM can become unstable in the plasma whose beta value is below no-wall beta limit.
Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Oyama, Naoyuki; Kojima, Atsushi; Tokuda, Shinji*; Yagi, Masatoshi
Nuclear Fusion, 51(7), p.073012_1 - 073012_9, 2011/07
We investigate numerically the destabilizing effect of a toroidal rotation on the edge localized MHD mode, which induces the large amplitude edge localized mode (ELM). As the results of this analysis, we reveal that the toroidal rotation with shear can destabilize this MHD mode, and the destabilization is caused by the difference between the plasma rotation frequency and the frequency of the unstable mode. Based on these results, we investigate numerically the stability of JT-60U type-I ELMy H-mode plasmas, and show that the toroidal rotation plays an important role for making the difference of ELM behavior observed in JT-60U plasmas with different plasma rotation profiles.
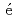n eigenmodesHirota, Makoto; Aiba, Nobuyuki
Nuclear Fusion, 51(7), p.073037_1 - 073037_10, 2011/07
Times Cited Count：2 Percentile：10.41(Physics, Fluids & Plasmas)Nonlinear mode coupling of the (shear) Alfv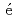n eigenmodes is studied both analytically and numerically to understand the effect of the magnetohydrodynamic (MHD) nonlinearity on the saturation mechanism. The energy transfer via the mode coupling can restrict the amplitude to a level that is estimated by the frequency mismatch and the coupling coefficient among the coupled modes. For the cases of cylindrical and toroidal geometries, new numerical codes are developed to calculate the coupling coefficient directly according to the Lagrangian theory of weakly nonlinear perturbations. It is shown that the shear Alfv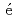n eigenmodes can couple with each other through the small compressional components of their eigenfunctions. By assuming low-
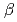plasma, an analytic estimation of the coupling coefficient (
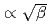) is derived in the cylindrical case. A coupling of reversed shear Alfv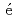n eigenmodes in toroidal geometry indicates a more effective energy transfer at a lower amplitude level owing to the enhanced compressional perturbations in the poloidal sidebands.
Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Oyama, Naoyuki; Kojima, Atsushi; Tokuda, Shinji*; Yagi, Masatoshi
Nuclear Fusion, 51(7), p.073012_1 - 073012_9, 2011/07
Times Cited Count：21 Percentile：65.79(Physics, Fluids & Plasmas)Mechanisms of plasma rotation on edge MHD stability is investigated numerically by introducing energies that are distinguished by physics. By comparing them, it is found that an edge localized MHD mode is destabilized by the difference between an eigenmode frequency and an equilibrium toroidal rotation frequency, which is induced by rotation shear. In addition, this destabilizing effect becomes effective in the shorter wavelength region. The effect of poloidal rotation on the edge MHD stability is also investigated. Under the assumption that the change of an equilibrium by poloidal rotation is negligible, it is identified numerically that poloidal rotation can have both the stabilizing effect and the destabilizing effect on the edge MHD stability, which depends on the direction of poloidal rotation. Numerical analysis demonstrates that these effects of plasma rotation in both toroidal and poloidal directions can play important roles on type-I ELM phenomena in JT-60U H-mode plasmas.
Hirota, Makoto
Journal of Plasma Physics, 77(5), p.589 - 615, 2011/01
Times Cited Count：5 Percentile：23.35(Physics, Fluids & Plasmas)A new equation of motion that governs weakly nonlinear phenomena inideal magnetohydrodynamics (MHD) is derived as a natural extension of the well-known linearized equation of motion for the displacement field. This derivation is made possible by expanding the MHD Lagrangianexplicitly up to third order with respect to the displacement of plasma, which necessitates an efficient use of the Lie series expansion. The resultant equation of motion (i.e., the Euler-Lagrange equation) includes a new quadratic force term which is responsible for various mode-mode coupling due to the MHD nonlinearity. The third-order potential energy serves to quantify the coupling coefficient among resonant three modes and its cubic symmetry proves the Manley-Rower elations. In contrast to earlier works, the coupling coefficient is expressed only by the displacement vector field, which is already familiar in the linear MHD theory, and both the fixed and free boundary cases are treated systematically.
Hirota, Makoto
Journal of Plasma and Fusion Research SERIES, Vol.9, p.463 - 470, 2010/08
Stabilization/destabilization of plasma by flow is a key issue inrecent fusion research and astrophysics. In order to gain a general understanding of this problem, it is informative to consider the modal energy (i.e., the energy of eigenmode) in the context of the stability theory of Hamiltonian mechanics, in which the negative energy mode is associated with the source of instability. In this work, we have developed a new method for transforming general linear perturbations to the action-angle variables, which enables us to evaluate the modal energy not only for each eigenmode, but also for acontinuum mode. Our method serves to provide a Hamiltonian interpretation of various instabilities in flowing plasmas.
Hirota, Makoto; Tokuda, Shinji*
Physics of Plasmas, 17(8), p.082109_1 - 082109_11, 2010/08
Times Cited Count：8 Percentile：30.82(Physics, Fluids & Plasmas)Invariance of wave action for eigenmodes and continuum modes around quasi-stationary equilibrium state is investigated in a general framework that allows for the ideal magnetohydrodynamic system and the Vlasov-Maxwell system. By utilizing the averaging method for the variational principle, the wave action of each mode is shown to be conserved if its frequency (spectrum) is sufficiently separated from other ones, whereas some conservative exchange of the wave action may occur among the modes with close frequencies. This general conservation law is, as an example, demonstrated for a situation where the Landau damping (or growth) occurs due to a resonance between an eigenmode and a continuum mode. The damping (or growth) rate is closely related to the spectral linewidth (= the phase mixing rate) of the continuum mode, which can be estimated by the invariance of wave action without invoking the conventional analytic continuation of the dispersion relation.
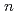dependence of the growth rate of the edge localized MHD modesAiba, Nobuyuki; Hirota, Makoto
Proceedings of 37th European Physical Society Conference on Plasma Physics (EPS 2010) (CD-ROM), 4 Pages, 2010/06
no abstracts in English
Aiba, Nobuyuki; Furukawa, Masaru*; Hirota, Makoto; Tokuda, Shinji
Nuclear Fusion, 50(4), p.045002_1 - 045002_13, 2010/04
Times Cited Count：22 Percentile：64.1(Physics, Fluids & Plasmas)In this paper, we investigate numerically the destabilizing effect of a toroidal rotation on the edge localized MHD mode, which induces the large amplitude edge localized mode (ELM). As the results of this analysis, we reveal that the toroidal rotation with shear can destabilize this MHD mode, and the destabilization is caused by the difference between the plasma rotation frequency and the frequency of the unstable mode, which mainly affects the pressure-driven component of the unstable mode. This destabilizing effect becomes more effective as the wave length of the mode becomes shorter, but such a MHD mode with short wave length is also stabilized by the sheared toroidal rotation due to the Doppler-shift at each flux surfaces. We clarify that the stability of the edge localized MHD mode, whose wave length is typically intermediate, is determined by the balance between these stabilizing and destabilizing effects.
Hirota, Makoto; Yoshida, Zensho*
Journal of Math-for-Industry (Internet), 1, p.123 - 130, 2009/10
Perturbations in a shear flow exhibit rather complex behavior - waves may grow algebraically even when the spectrum of disturbances is entirely neutral (no exponential instability). A shear flow brings about non-selfadjoint property, invalidating the standard notion of dispersion relations, and it also produces a continuous spectrum that is a characteristic entity in an infinite-dimension phase space. This paper solves an initial value problem using the Laplace transform and presents a new-type of algebraic instability that is caused by resonant interaction between acoustic modes (point spectrum) and vortical continuum mode (continuous spectrum). Such a resonance is possible when variation of velocity shear is comparable to sound speed.
Hirota, Makoto
Plasma Science and Technology, 11(4), p.409 - 412, 2009/08
Times Cited Count：4 Percentile：16.48(Physics, Fluids & Plasmas)Stability of magnetohydrodynamic (MHD) waves subject to Alfv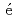n and sound resonances and small resistivity at a conductive wall is formally discussed in terms of wave energy (or, more precisely, wave action). Negative energy wave, which may exist in the presence of mean flow, is shown to be destabilized by the resistive wall, where its growth rate is characterized by the energy dissipation rate. The effect of resonance is examined as well based on a recent knowledge of wave energy for Alfv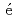n and sound continuum modes. Resonant coupling between an eigenmode and a continuum mode having the same sign of energy results in phase mixing (or continuum) damping. In contrast, if their signs are opposite, such resonance triggers an instability.
Hirota, Makoto; Fukumoto, Yasuhide*
Physics of Plasmas, 15(12), p.122101_1 - 122101_11, 2008/12
Times Cited Count：14 Percentile：46.66(Physics, Fluids & Plasmas)Action-angle variables corresponding to singular (or improper) eigenmodes are rigorously formulated for the Alfv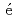n and slow (or cusp) continuous spectra of ideal magnetohydrodynamics. The perturbation energy is then transformed into the normal form, namely, the eigenfrequency multiplied by the action variable. It is shown that the Laplace transform approach expedites this action-angle formulation more efficiently than the existing ones devoted to other kinds of continuous spectra. The presence of flow that is either non-parallel to the magnetic field or supersonic at some places brings about singular eigenmodes with negative energy. The Alfv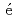n and slow singular eigenmodes are neutrally stable even in the presence of any external potential fields, but may cause instability when coupled with another singular or non-singular eigenmode with the opposite sign of energy.
O reflectorHirota, Jitsuya; Kuroi, Hideo; Goto, Yorio; Furuhashi, Akira; Yasuno, Takehiko; Yamamoto, Ken; Mitani, Hiroshi; Obu, Makoto; Ichimori, Toshihiro; Koyama, Kinji; et al.
JAERI 1034, 50 Pages, 1962/08
no abstracts in English
Hirota, Makoto; Tokuda, Shinji; Fukumoto, Yasuhide*
no journal, ,
Hirota, Makoto; Tokuda, Shinji
no journal, ,
Effects of flows on the MHD instabilities have been drawing considerable attention. The standard energy principle, however, is not applicable to flowing plasmas, because waves with negative energy may be stable in such moving media. Additional theoretical framework is needed to study how negative energy modes occur and trigger instabilities, and we discuss it by taking the resistive wall mode as an example. The external kink mode, being stabilized by the wall, assumes negative energy when the Doppler shift due to the flow exceeds a critical value. The energy dissipation at the resistive wall destabilizes this mode. To attain stability condition, another physical mechanism different from dissipation must be taken into account.
Hirota, Makoto
no journal, ,
Effects of flows on the MHD instabilities have been drawing considerable attention. The standard energy principle, however, is not applicable to flowing plasmas, because waves with negative energy may be stable in such moving media. The action-angle representation for the MHD waves is useful for studying how negative energy modes occur and trigger instabilities, and we discuss it by taking the resistive wall mode (RWM) as an example. The external kink mode, being stabilized by the wall, assumes negative energy when the Doppler shift due to the flow exceeds a critical value. The energy dissipation at the resistive wall destabilizes this mode. To attain stability condition, another physical mechanism different from dissipation must be taken into account.
