粒子法による熱伝導-対流遷移の研究

渡辺 正; 蕪木 英雄

JAERI-Research 96-046, 50 Pages, 1996/09

JAERI-Research-96-046.pdf:1.58MB

代表的な粒子法である直接シミュレーションモンテカルロ法及び分子動力学法を用いてレイリーベナール系をシミュレートし、マクロな流れ場における熱伝導-対流遷移をミクロレベルから考察した。統計的手法であるモンテカルロ法により得られた臨界レイリー数は、流体方程式の線形安定性解析により得られるものと一致し、マクロな流れの安定性がミクロレベルの粒子法により定量的に扱うことができることがわかった。また、遷移過程では温度や流速の変動量の相関が、明確な熱伝導及び対流状態におけるものより強くなっていることが明らかとなった。さらに決定論的手法である分子動力学法により原子のカオス運動をリアプノフ指数を用いて調べたところ、大規模な秩序運動としての対流渦が流れ場に現れると、個々の原子のカオス運動は増加することが明らかとなった。

直接シミュレーションモンテカルロコードPstc-2dの並列化

岸田 則生*; 横川 三津夫; 渡辺 正; 蕪木 英雄

JAERI-Data/Code 96-008, 20 Pages, 1996/03

JAERI-Data-Code-96-008.pdf:1.1MB

2次元Rayleigh-Benard流れを直接シミュレーションモンテカルロ(DSMC)法でシミュレートするPstc-2dコードをParagon上で並列化した。並列化にはParagon固有のメッセージパッシングインターフェイスであるNXライブラリが使用された。DSMC法はプロセッサ数nに対してO(n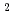)のメッセージ転送回数を要求するので、nが大きい時の並列化効率はあまり良くない。計算精度をある程度犠牲にするもののメッセージ転送回数がO(n)である新たなメッセージ転送アルゴリズムが提案される。PVMとNXライブラリによる並列化が比較され、後者の方が3倍速いことが判明した。Paragonの大メモリ空間を利用して、アスペクト比が8のRayleigh-Benard流のシミュレーションが可能になった。得られたロール数は連続流モデルから期待される結果と良く一致した。

直接シミュレーションモンテカルロ法によるRayleigh-Benard不安定性の研究

渡辺 正; 蕪木 英雄; 町田 昌彦*; 横川 三津夫

Therm. Sci. Eng., 2(4), p.17 - 24, 1994/00

熱伝導から対流熱伝達への遷移が生じるRayleigh-Benard不安定性を、直接シミュレーションモンテカルロ法により調べた。基礎方程式と計算手法を詳しく記述し、分子運動のレベルの計算により得られる臨界レイリー数が、巨視的な流体方程式の線形不安定性理論から導かれる値と一致することを示した。さらに、臨界レイリー数近傍の条件における遷移過程で流れ場が熱伝導状態を示していても、温度変動の空間的な相関は既に対流状態への移行を示していること、変動の影響の及ぶ範囲を示す特性距離は、安定な熱伝導あるいは対流状態では小さく、遷移過程でのみ大きくなることが示された。