Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
横田 光史
Physica A, 363(2), p.161 - 170, 2006/03
被引用回数：6 パーセンタイル：41.18(Physics, Multidisciplinary)スピングラス転移温度近傍におけるイジングスピングラス模型をクラスター近似を用いて調べた。スピングラス秩序パラメーター関数及び磁場中においてレプリカ対称性が破れるAT線を求めた。
横田 光史
Progress of Theoretical Physics Supplement, (157), p.90 - 93, 2005/06
外場中のポッツグラス模型は、分子からなる結晶における方向性グラスにストレスがかった場合などのモデルと考えられる。このモデルに対する平均場理論をグラスのランダムネスに対する平均をとる数学的操作であるレプリカ法を用いて調べた。温度を下げていくと、外場と垂直方向への凍結によるグラス転移が起こる。その転移温度近くでのレプリカ対称性の破れのパターンを解析的に求めた。レプリカ対称性の破れのパターンは多くの凍結状態の間の関係を示している。ポッツ成分の数が3のときは、連続的なレプリカ対称性の破れがおこる。ポッツ成分の数が4のときは、1ステップの不連続的なレプリカ対称性の破れとなる。さらに、ポッツ成分の数が5以上の場合には、グラスオーダーパラメーターが不連続となるような転移となることを示した。これらの結果は、グラス転移の性質は定性的にはゼロ磁場の場合と対応するが、その対応はポッツ成分の数をシフトすることで得られるものであることを示している。
横田 光史
Journal of Physics; Condensed Matter, 10(23), p.5179 - 5186, 1998/00
被引用回数：0 パーセンタイル：0.00(Physics, Condensed Matter)臨界現象において、平均場近似的振る舞いは、ゆらぎによって修正される。ランダム磁場イジング模型においては、ランダムさに起因するゆらぎが重要である。ここでは、2種類の平均場近似に基づく、ギンツブルグのゆらぎの重要性に関する基準を議論した。一つ目は、レプリカ法を用いた平均場近似であり、二つ目は、場所に依存する平均場近似である。ランダム磁場イジング模型に対する臨界現象の様子を場所に依存する平均場近似を用いて求めることの正当性を示した。
横田 光史
Physics Letters A, 230(1-2), p.117 - 120, 1997/06
被引用回数：1 パーセンタイル：19.10(Physics, Multidisciplinary)横磁場中のランダム磁場イジング模型における温度ゼロでの量子相転移を調べた。相関関数に対するself-consistent screening approximationを用いて、強磁性相転移点においてレプリカ対称性が破れていることを示した。
横田 光史
Journal of Physics; Condensed Matter, 4, p.2615 - 2622, 1992/00
被引用回数：11 パーセンタイル：56.59(Physics, Condensed Matter)S=1の結晶場中におけね一般化されたSKイジングスピングラス模型について、スピングラス相と1次相転移を調べた。この模型に対して、平均場方程式を導き、それを数値的に解いた。一次転移線近くでは、P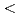i=
Si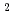
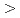のダブルピーク構造が重要であることを示した。この相転移は、定性的にみて、基底状態での相転移に似ている。
