Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
横山 賢治; 山本 章夫*; 北田 孝典*
Journal of Nuclear Science and Technology, 55(3), p.319 - 334, 2018/03
被引用回数:8 パーセンタイル:56.73(Nuclear Science & Technology)次元削減に関する技術を応用して炉定数調整法の新しい理論式を導出した。この新しい理論式を次元削減炉定数調整法(DRCA)として提案する。DRCAの導出は最小分散不偏推定(MVUE)に基づいており、正規分布の仮定を必要としない。DRCAの結果は、ユーザが定義する行列で指定する次元削減後の特徴空間に依存する。このため、DRCA1, DRCA2, DRCA3という3種類の次元削減炉定数調整法を提案する。数式による検討及び数値計算による検証を行ったところ、DRCA2は、現在広く使われている炉定数調整法と等価になることが分かった。更に、DRCA3は、以前の研究で提案した最小分散不偏推定に基づく炉定数調整法と等価になることが分かった。
Hieu, N. M.*; 熊沢 蕃
JAERI-Research 2000-065, 28 Pages, 2001/02
本報告書は医療分野における放射線防護体系と線量分布の関係を調べるため、ベトナム原子力委員会(VAEC)第103病院32名の線量データを対数正規及び混成対数正規モデルを適用して解析したものである。解析した1994年の月線量データはVAEC制定基準4.2mSv/月に比べ十分低く、全線量範囲で対数正規性を示す反面、大多数のデータが存在する0.3mSv/月以下の線量域に着目すると、被ばく低減効果を反映する混成対数正規性が確認された。月線量データを職種,線源,作業者または月別に層別化しても分布則性の傾向は同じであった。年線量データも全線量域で対数正規性の反面、1mSv以下では同様に被ばく低減を反映する混成対数正規性を示した。これより、病院における線量分布にも注意深く分析すれば、実際の被ばく低減努力の効果が確認でき、防護の有効性評価が可能になることが知られた。
角谷 浩享*; 塩田 雅之*; 末富 英一*; 内藤 俶孝; 黒澤 正義
JAERI-Research 95-033, 31 Pages, 1995/03
有機溶剤を減速材にもつMOX燃料棒体系の臨界実験は従来、有機溶剤の熱中性子散乱核を用いて解析されてはいない。通常有機溶剤中の水素原子に対する散乱核は軽水中の水素に関するもので代用されている。これは有機溶剤に関して熱中性子散乱断面積の信頼できるデータが存在しなかったためである。そこで有機溶剤TBP(tributyl phosphate)に関する全断面の実験値を再現するような散乱核を作成し、これを用いて32vol%のn-ドデカンの混合液を減速材にもつMOX燃料棒体系の臨界実験を解析した。臨界解析はモンテカルロ法臨界解析コードMULTI-KENO及びMGCL多群定数ライブラリーを用いて行った。新しい散乱核を用いた実効増倍率は従来の結果より小さく、かつ実験値との良い一致を示した。また、軽水の散乱核を用いた従来の解析との差は0.5%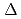 Kと小さかったが、臨界固有値の燃料棒格子幅依存性が改善された。
Kと小さかったが、臨界固有値の燃料棒格子幅依存性が改善された。
熊沢 蕃; 大橋 靖雄*
応用統計学, 15(1), p.1 - 14, 1986/00
混成対数正規分布とは、正値確率変数Xに対して、パラメータ を含む変換ln
を含む変換ln X+
X+ Xが正規分布N(
Xが正規分布N(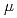 ,
,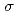
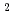 )に従う分布のことである。本分布は放射線に被曝する作業に従事する作業者の線量分布が、被曝低減管理の影響を受けて管理の弱い場合は対数正規分布側へ、また管理の強い場合は正規分布へ近づくことをモデル化したものである。本論文では混成対数正規分布の性質と発生機構を述べ、線量分布および他の種類(使用水量、雨量、砂粒径など)の分布へのあてはめ例を示した後、それらの分布の背後にある現象を分布形の違いから解釈できることを示す。このように本分布は線量分布以外にも広く適用できるばかりでなく、本分布の極限分布として一方に対数正規分布を持ち、他方に正規分布を持つ新しい形式の分布システムを構成する。
)に従う分布のことである。本分布は放射線に被曝する作業に従事する作業者の線量分布が、被曝低減管理の影響を受けて管理の弱い場合は対数正規分布側へ、また管理の強い場合は正規分布へ近づくことをモデル化したものである。本論文では混成対数正規分布の性質と発生機構を述べ、線量分布および他の種類(使用水量、雨量、砂粒径など)の分布へのあてはめ例を示した後、それらの分布の背後にある現象を分布形の違いから解釈できることを示す。このように本分布は線量分布以外にも広く適用できるばかりでなく、本分布の極限分布として一方に対数正規分布を持ち、他方に正規分布を持つ新しい形式の分布システムを構成する。
松井 浩; 渡辺 宏道*; 国分 守信
JAERI-M 8757, 41 Pages, 1980/03
放射線管理データを解析する場合、種々のデータが分布則に従っているかを決定することは重要なことである。それぞれのデータの従う分布則を判別する一つの方法として、種々の確立紙上における異なる分布関数グラフの形状を把握することにより、分布則を定性的に判別する方法を検討した。特に、利用し易い対数正規確立紙上でのグラフの形状およびデータの統計処理過程で得られる情報をできる限り利用して分布則を確定する方法を示した。