Study on calculation methods for the effective delayed neutron fraction

実効遅発中性子割合に対する計算手法の検討

Irwanto, D.*; 千葉 豪; 長家 康展  ; 小原 徹*

Irwanto, D.*; Chiba, Go; Nagaya, Yasunobu; Obara, Toru*

実効遅発中性子割合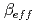は原子炉の動的な振る舞いを支配する重要なパラメータの一つである。これまでに、幾つかのモンテカルロ法に基づいた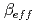の計算方法が提案されている。本研究では、それらの方法の精度を定量的に評価するため、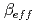の計算手法に着目し、裸炉心,反射体付き炉心,MASURCA-R2, MASURCA-ZONA2, FCA XIX-1, XIX-2, XIX-3といった高速炉心を対象に検討を行った。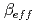について、基本値(均一重み),一般的な定義,名内による定義,Meulekampによる定義に基づいて計算し、その各々の比較を行った。その結果、一般的な定義,名内による定義,Meulekampによる定義に基づく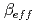の値は最大で10%異なる場合があること、均一重みの値は幾つかの体系で大幅に大きな値となること、すべての体系で、Meulekampによる定義は名内の定義と比較して大きな値となること、を示した。さらに、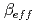に対する複数世代の効果を評価し、一般的な定義に基づく値を求めるためには、それが無視できないことを示した。

It is rather difficult to measure the effective delayed neutron fraction with experiments, so it becomes important to obtain their accurate calculation values. We study calculation methods for the effective delayed neutron fraction by analyzing various fast neutron systems including the bare spherical systems (Godiva, Jezebel, Skidoo, Jezebel-240), the reflective spherical systems (Popsy, Topsy, Flattop-23), MASURCA-R2 and MASURCA-ZONA2, and FCA XIX-1, XIX-2 and XIX-3. These analyses are performed by using SLAROM-UF and CBG for the deterministic method and MVP-II for the Monte Carlo method. We calculate the effective delayed neutron fraction with various definitions such as the fundamental value, the standard definition, Nauchi's definition and Meulekamp's definition, and compare these results with each other.