Overview of toroidal momentum transport

トロイダル運動量輸送のオーバービュー

Peeters, A. G.*; Angioni, C.*; Bortolon, A.*; Camenen, Y.*; Casson, F. J.*; Duval, B.*; Fiederspiel, L.*; Hornsby, W. A.*; 井戸村 泰宏   ; Hein, T.*; Kluy, N.*; Mantica, P.*; Parra, F. I.*; Snodin, A. P.*; Szepesi, G.*; Strintzi, D.*; Tala, T.*; Tardini, G.*; de Vries, P.*; Weiland, J.*

Peeters, A. G.*; Angioni, C.*; Bortolon, A.*; Camenen, Y.*; Casson, F. J.*; Duval, B.*; Fiederspiel, L.*; Hornsby, W. A.*; Idomura, Yasuhiro; Hein, T.*; Kluy, N.*; Mantica, P.*; Parra, F. I.*; Snodin, A. P.*; Szepesi, G.*; Strintzi, D.*; Tala, T.*; Tardini, G.*; de Vries, P.*; Weiland, J.*

Toroidal momentum transport mechanisms are reviewed and put in a broader perspective. The generation of a finite momentum flux is closely related with the breaking of symmetry (parity) along the field. The symmetry argument allows for the systematic identification of possible transport mechanisms. Those that appear to lowest order in the normalized Larmor radius (the diagonal part, Coriolis pinch, E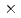B shearing, particle flux, and up-down asymmetric equilibriums) are reasonably well understood. At higher order, thought to be of importance in the plasma edge, the theory is still under development.