Radially local approximation of the drift kinetic equation

ドリフト運動論方程式の径方向局所近似

洲鎌 英雄*; 松岡 清吉 ; 佐竹 真介*; 菅野 龍太郎*

Sugama, Hideo*; Matsuoka, Seikichi; Satake, Shinsuke*; Kanno, Ryutaro*

ドリフト運動論方程式について、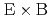及び磁気面に沿ったドリフトの両者を含む新たな径方向局所近似モデルを構築した。このモデルは保存系で表現されており定常解を得るための追加のソース項を必要としない為、数値計算に適したモデルとなっている。このモデルから得られる解は、準対称性を持つ磁場配位における性質として重要な、衝突性粒子輸送の両極性条件を満たす。また、逆に、両極性条件を故意に破るような近似モデルを考えた場合には、衝突性輸送によるエントロピー生成の正値性及び拡散係数のオンサーガー対称性が得られることを示した。

A novel radially local approximation of the drift kinetic equation is presented. The new drift kinetic equation that includes both 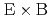and tangential magnetic drift terms is written in the conservative form and it has favorable properties for numerical simulation that any additional terms for particle and energy sources are unnecessary for obtaining stationary solutions under the radially local approximation. These solutions satisfy the intrinsic ambipolarity condition for neoclassical particle fluxes in the presence of quasisymmetry of the magnetic field strength. Also, another radially local drift kinetic equation is presented, from which the positive definiteness of entropy production due to neoclassical transport and Onsager symmetry of neoclassical transport coefficients are derived while it sacrifices the ambipolarity condition for neoclassical particle fluxes in axisymmetric and quasi-symmetric systems.