Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
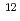 C
C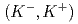 reaction at 1.8 GeV/
reaction at 1.8 GeV/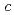 with the Superconducting Kaon spectrometer
with the Superconducting Kaon spectrometer市川 裕大; 藤田 真奈美; 長谷川 勝一; 今井 憲一*; 七村 拓野; 成木 恵; 佐藤 進; 佐甲 博之; 田村 裕和; 谷田 聖; et al.
Progress of Theoretical and Experimental Physics (Internet), 2024(9), p.091D01_1 - 091D01_13, 2024/09
被引用回数:0 パーセンタイル:0.00(Physics, Multidisciplinary)We conducted a measurement of the inclusive missing-mass spectrum in the  C
C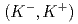 reaction at an incident beam momentum of 1.8 GeV/
reaction at an incident beam momentum of 1.8 GeV/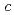 . This measurement was carried out utilizing the Superconducting Kaon Spectrometer (SKS) and the K1.8 beamline spectrometer at the Hadron Experimental Hall in J-PARC. Remarkably, our experimental setup yielded an exceptionaly good energy resolution of 8.2 MeV (FWHM), enabling us to observe significant enhancements in the vicinity of the
. This measurement was carried out utilizing the Superconducting Kaon Spectrometer (SKS) and the K1.8 beamline spectrometer at the Hadron Experimental Hall in J-PARC. Remarkably, our experimental setup yielded an exceptionaly good energy resolution of 8.2 MeV (FWHM), enabling us to observe significant enhancements in the vicinity of the 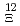 Be threshold region. In order to estimate the spectrum information, we employed several fitting parameters assumptions. The best agreement with the spectrum shape was obtained with combining quasi-free (QF) component and two-Gaussian functions, with the experimental resolution
Be threshold region. In order to estimate the spectrum information, we employed several fitting parameters assumptions. The best agreement with the spectrum shape was obtained with combining quasi-free (QF) component and two-Gaussian functions, with the experimental resolution 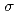 being held constant. The peak positions were obtained to be
being held constant. The peak positions were obtained to be 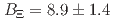 (stat.)
(stat.) 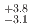 (syst.) MeV and
(syst.) MeV and 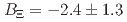 (stat.)
(stat.) 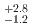 (syst.) MeV. Another model assumption, utilizing quasi-free (QF) and one Breit-Wigner function with
(syst.) MeV. Another model assumption, utilizing quasi-free (QF) and one Breit-Wigner function with 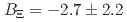 (stat.)
(stat.) 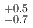 (syst.) MeV and
(syst.) MeV and 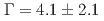 (stat.)
(stat.) 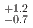 (syst.) MeV, also yielded a similar
(syst.) MeV, also yielded a similar 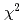 value.
value.
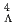 H hypernucleus using in-flight
H hypernucleus using in-flight 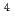 He
He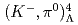 H reaction
H reaction赤石 貴也; 橋本 直; 谷田 聖; 他35名*
Physics Letters B, 845, p.138128_1 - 138128_4, 2023/10
被引用回数:1 パーセンタイル:25.07(Astronomy & Astrophysics)We present a new measurement of the 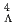 H hypernuclear lifetime using in-flight
H hypernuclear lifetime using in-flight 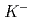 +
+ 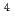 He
He 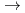
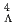 H +
H + 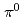 reaction at the J-PARC hadron facility. We demonstrate, for the first time, the effective selection of the hypernuclear bound state using only the
reaction at the J-PARC hadron facility. We demonstrate, for the first time, the effective selection of the hypernuclear bound state using only the 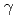 -ray energy decayed from
-ray energy decayed from 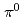 . This opens the possibility for a systematic study of isospin partner hypernuclei through comparison with data from (
. This opens the possibility for a systematic study of isospin partner hypernuclei through comparison with data from (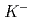 ,
, 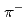 ) reaction. As the first application of this method, our result for the
) reaction. As the first application of this method, our result for the 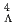 H lifetime,
H lifetime,  , is one of the most precise measurements to date. We are also preparing to measure the lifetime of the hypertriton (
, is one of the most precise measurements to date. We are also preparing to measure the lifetime of the hypertriton (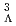 H) using the same setup in the near future.
H) using the same setup in the near future.
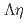 threshold in the
threshold in the 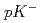 mass spectrum with
mass spectrum with 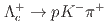 decays
decaysYang, S.*; 谷田 聖; Belle Collaboration*; 他196名*
Physical Review D, 108(3), p.L031104_1 - L031104_6, 2023/08
被引用回数:5 パーセンタイル:57.15(Astronomy & Astrophysics)We observe a narrow peaking structure in the 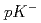 invariant-mass spectrum near the
invariant-mass spectrum near the 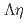 threshold. The peak is clearly seen in 1.5 million events of
threshold. The peak is clearly seen in 1.5 million events of 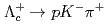 decay using the
decay using the 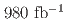 data sample collected by the Belle detector at the KEKB asymmetric-energy
data sample collected by the Belle detector at the KEKB asymmetric-energy 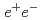 collider. We try two approaches to explain this structure: as a new resonance and as a cusp at the
collider. We try two approaches to explain this structure: as a new resonance and as a cusp at the 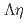 threshold. The best fit is obtained with a coherent sum of a Flatt
threshold. The best fit is obtained with a coherent sum of a Flatt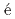 function and a constant background amplitude with the
function and a constant background amplitude with the 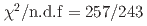 (
(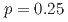 ), while the fits to Breit-Wigner functions are unfavored by more than 7
), while the fits to Breit-Wigner functions are unfavored by more than 7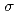 . The best fit explains the structure as a cusp at the
. The best fit explains the structure as a cusp at the 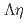 threshold, and the obtained parameters are consistent with the known properties of
threshold, and the obtained parameters are consistent with the known properties of 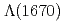 . The observation gives the first identification of a threshold cusp in hadrons from the spectrum shape.
. The observation gives the first identification of a threshold cusp in hadrons from the spectrum shape.
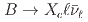 decays with the Belle II experiment
decays with the Belle II experimentAbudin n, F.*; 谷田 聖; Belle II Collaboration*; 他413名*
n, F.*; 谷田 聖; Belle II Collaboration*; 他413名*
Physical Review D, 107(7), p.072002_1 - 072002_24, 2023/04
被引用回数:9 パーセンタイル:76.22(Astronomy & Astrophysics)We present measurements of the first to fourth moments of the lepton mass squared 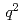 of
of 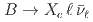 decays for
decays for 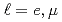 and with
and with 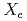 a hadronic system containing a charm quark. These results use a sample of electron-positron collisions at the
a hadronic system containing a charm quark. These results use a sample of electron-positron collisions at the 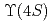 resonance corresponding to
resonance corresponding to 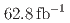 of integrated luminosity and collected by the Belle II experiment in 2019 and 2020. To identify the
of integrated luminosity and collected by the Belle II experiment in 2019 and 2020. To identify the 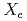 system and reconstruct
system and reconstruct 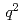 , one of the
, one of the 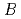 mesons from an
mesons from an 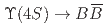 decay is fully reconstructed in a hadronic decay mode using a multivariate
decay is fully reconstructed in a hadronic decay mode using a multivariate 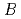 tagging algorithm. We report raw and central moments for
tagging algorithm. We report raw and central moments for 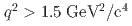 up to
up to 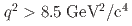 , probing up to 77% of the accessible
, probing up to 77% of the accessible 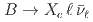 phase space. This is the first measurement of moments in the experimentally challenging range of
phase space. This is the first measurement of moments in the experimentally challenging range of ![$$[ 1.5, 2.5 ] , mathrm{GeV^2/c^4}$$](/search/images/ERNSAMJOGUWCAMROGUQF0IC2FQQFY1LBORUHE1L1I3SVMXRSF3RV2ND3EQ.gif) .
.
 at Belle
at BelleYin, J. H.*; 谷田 聖; Belle Collaboration*; 他193名*
Physical Review D, 107(5), p.052004_1 - 052004_8, 2023/03
被引用回数:3 パーセンタイル:40.72(Astronomy & Astrophysics)We present a search for the decay 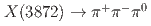 in the
in the 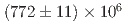
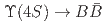 data sample collected at the Belle detector, where the
data sample collected at the Belle detector, where the 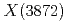 is produced in
is produced in 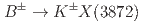 and
and 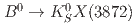 decays. We do not observe a signal, and set 90% credible upper limits for two different models of the decay processes: if the decay products are distributed uniformly in phase space,
decays. We do not observe a signal, and set 90% credible upper limits for two different models of the decay processes: if the decay products are distributed uniformly in phase space, 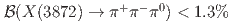 ; if
; if 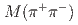 is concentrated near the mass of the
is concentrated near the mass of the 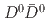 pair in the process
pair in the process 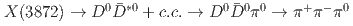 ,
, 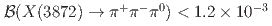 .
.
Ahn, J. K.*; 長谷川 勝一; 今井 憲一*; 佐甲 博之; 佐藤 進; 谷田 聖; 他10名*
Nuclear Instruments and Methods in Physics Research A, 1047, p.167775_1 - 167775_13, 2023/02
被引用回数:1 パーセンタイル:17.31(Instruments & Instrumentation)We have constructed a conduction-cooled superconducting dipole magnet for the Hyperon spectrometer at Japan Proton Accelerator Research Complex (J-PARC). The magnet is a Helmholtz-type dipole magnet with two circular coils with a radius of 500 mm separated by 500 mm. It provides a uniform magnetic field of 1.0 T or higher in a volume of  mm
mm 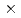 600 mm, covering the drift region of a time projection chamber (TPC). Owing to the target location inside the TPC, the Hyperon spectrometer has a broad angular coverage with a nearly
600 mm, covering the drift region of a time projection chamber (TPC). Owing to the target location inside the TPC, the Hyperon spectrometer has a broad angular coverage with a nearly 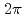 solid angle. We have successfully excited the magnet up to 1.3 T. At 1.0 T, we operated it stably for more than 1 week in single-magnet configuration and double-magnet configuration with a normal-conducting 0.7-T dipole magnet located 30 cm apart. The measured magnetic field distribution in the TPC volume is consistent with the calculated field map.
solid angle. We have successfully excited the magnet up to 1.3 T. At 1.0 T, we operated it stably for more than 1 week in single-magnet configuration and double-magnet configuration with a normal-conducting 0.7-T dipole magnet located 30 cm apart. The measured magnetic field distribution in the TPC volume is consistent with the calculated field map.
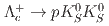 and
and 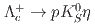 at Belle
at BelleLi, L. K.*; 谷田 聖; Belle Collaboration*; 他204名*
Physical Review D, 107(3), p.032004_1 - 032004_9, 2023/02
被引用回数:5 パーセンタイル:57.15(Astronomy & Astrophysics)We present a study of a singly Cabibbo-suppressed decay 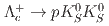 and a Cabibbo-favored decay
and a Cabibbo-favored decay 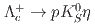 based on 980
based on 980 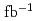 of data collected by the Belle detector, operating at the KEKB energy-asymmetric
of data collected by the Belle detector, operating at the KEKB energy-asymmetric 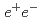 collider. We measure their branching fractions relative to
collider. We measure their branching fractions relative to 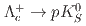 :
: 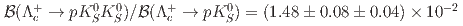 and
and 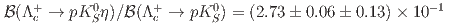 . Combining with the world average
. Combining with the world average 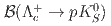 , we have the absolute branching fractions:
, we have the absolute branching fractions: 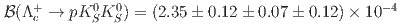 and
and 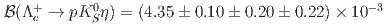 . The first and second uncertainties are statistical and systematic, respectively, while the third ones arise from the uncertainty on
. The first and second uncertainties are statistical and systematic, respectively, while the third ones arise from the uncertainty on 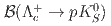 . The mode
. The mode 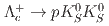 is observed for the first time and has a statistical significance of
is observed for the first time and has a statistical significance of 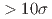 . The branching fraction of
. The branching fraction of 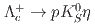 has been measured with a threefold improvement in precision over previous results and is found to be consistent with the world average.
has been measured with a threefold improvement in precision over previous results and is found to be consistent with the world average.
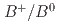 production ratio in
production ratio in 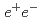 collisions at the
collisions at the 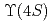 resonance using
resonance using 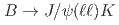 decays at Belle
decays at BelleChoudhury, S.*; 谷田 聖; Belle Collaboration*; 他198名*
Physical Review D, 107(3), p.L031102_1 - L031102_6, 2023/02
被引用回数:12 パーセンタイル:72.68(Astronomy & Astrophysics)We measure the ratio of branching fractions for the 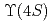 decays to
decays to 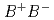 and
and 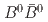 using
using 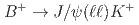 and
and 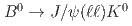 samples, where
samples, where 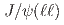 stands for
stands for 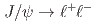 (
(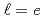 or
or 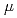 ), with
), with 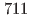 fb
fb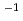 of data collected at the
of data collected at the 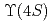 resonance with the Belle detector. We find the decay rate ratio of
resonance with the Belle detector. We find the decay rate ratio of 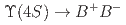 over
over 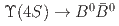 to be
to be  , which is the most precise measurement to date. The first and second uncertainties are statistical and systematic, respectively, and the third uncertainty is systematic due to the assumption of isospin symmetry in
, which is the most precise measurement to date. The first and second uncertainties are statistical and systematic, respectively, and the third uncertainty is systematic due to the assumption of isospin symmetry in 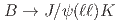 .
.
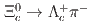 at Belle
at BelleTang, S. S.*; 谷田 聖; Belle Collaboration*; 他173名*
Physical Review D, 107(3), p.032005_1 - 032005_6, 2023/02
被引用回数:4 パーセンタイル:49.66(Astronomy & Astrophysics)Based on a data sample of 983 fb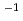 collected with the Belle detector at the KEKB asymmetric-energy
collected with the Belle detector at the KEKB asymmetric-energy 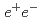 collider, we present the study of the heavy-flavor-conserving decay
collider, we present the study of the heavy-flavor-conserving decay 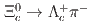 with
with 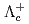 reconstructed via its
reconstructed via its 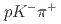 decay mode. The branching fraction ratio
decay mode. The branching fraction ratio 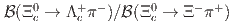 is measured to be
is measured to be 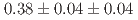 . Combing with the world average value of
. Combing with the world average value of 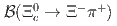 , the branching fraction
, the branching fraction 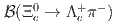 is deduced to be
is deduced to be 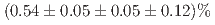 . Here, the uncertainties above are statistical, systematic, and from
. Here, the uncertainties above are statistical, systematic, and from 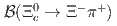 , respectively.
, respectively.
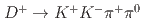 and
and 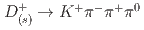 at Belle
at BelleLi, L. K.*; 谷田 聖; Belle Collaboration*; 他197名*
Physical Review D, 107(3), p.033003_1 - 033003_9, 2023/02
被引用回数:0 パーセンタイル:0.00(Astronomy & Astrophysics)We present measurements of the branching fractions for the singly Cabibbo-suppressed decays 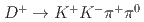 and
and 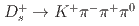 , and the doubly Cabibbo-suppressed decay
, and the doubly Cabibbo-suppressed decay 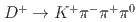 , based on 980
, based on 980 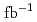 of data recorded by the Belle experiment at the KEKB
of data recorded by the Belle experiment at the KEKB 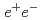 collider. We measure these modes relative to the Cabibbo-favored modes
collider. We measure these modes relative to the Cabibbo-favored modes 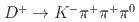 and
and 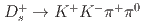 . Our results for the ratios of branching fractions are
. Our results for the ratios of branching fractions are 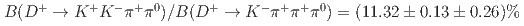 ,
, 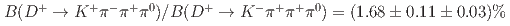 , and
, and 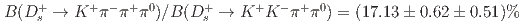 , where the uncertainties are statistical and systematic, respectively. The second value corresponds to
, where the uncertainties are statistical and systematic, respectively. The second value corresponds to 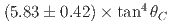 , where
, where 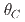 is the Cabibbo angle; this value is larger than other measured ratios of branching fractions for a doubly Cabibbo-suppressed charm decay to a Cabibbo-favored decay. Multiplying these results by world average values for
is the Cabibbo angle; this value is larger than other measured ratios of branching fractions for a doubly Cabibbo-suppressed charm decay to a Cabibbo-favored decay. Multiplying these results by world average values for 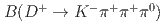 and
and 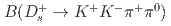 yields
yields 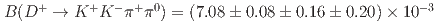 ,
, 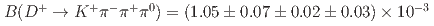 , and
, and 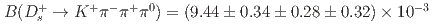 , where the third uncertainty is due to the branching fraction of the normalization mode. The first two results are consistent with, but more precise than, the current world averages. The last result is the first measurement of this branching fraction.
, where the third uncertainty is due to the branching fraction of the normalization mode. The first two results are consistent with, but more precise than, the current world averages. The last result is the first measurement of this branching fraction.
 and
and 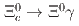
Li, Y.*; 谷田 聖; Belle Collaboration*; 他187名*
Physical Review D, 107(3), p.032001_1 - 032001_11, 2023/02
被引用回数:2 パーセンタイル:29.46(Astronomy & Astrophysics)We present the first search for the weak radiative decays 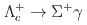 and
and 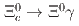 using a data sample of 980~fb
using a data sample of 980~fb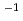 collected by the Belle detector operating at the KEKB asymmetric-energy
collected by the Belle detector operating at the KEKB asymmetric-energy 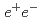 collider. There are no evident
collider. There are no evident 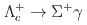 or
or 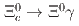 signals. Taking the decays
signals. Taking the decays 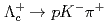 and
and 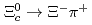 as normalization channels, the upper limits at 90% credibility level on the ratios of branching fractions
as normalization channels, the upper limits at 90% credibility level on the ratios of branching fractions 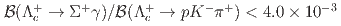 and
and 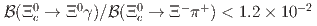 are determined. We obtain the upper limits at 90% credibility level on the absolute branching fractions
are determined. We obtain the upper limits at 90% credibility level on the absolute branching fractions 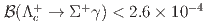 and
and 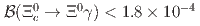 .
.
 measured in
measured in 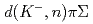 reactions
reactions相川 脩*; 橋本 直; 谷田 聖; 他73名*
Physics Letters B, 837, p.137637_1 - 137637_8, 2023/02
被引用回数:10 パーセンタイル:79.31(Astronomy & Astrophysics)We measured a set of 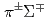 ,
, 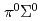 , and
, and 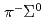 invariant mass spectra below and above the
invariant mass spectra below and above the 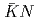 mass threshold in
mass threshold in 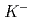 -induced reactions on deuteron. We deduced the
-induced reactions on deuteron. We deduced the 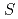 -wave
-wave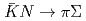 and
and 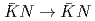 scattering amplitudes in the isospin 0 channel in the framework of a
scattering amplitudes in the isospin 0 channel in the framework of a 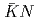 and
and 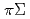 coupled channel. We find that a resonance pole corresponding to
coupled channel. We find that a resonance pole corresponding to  is located at 1417.7
is located at 1417.7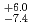 (fitting errors)
(fitting errors)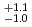 (systematic errors) +
(systematic errors) + 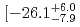 (fitting errors)
(fitting errors)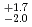 (systematic errors)]
(systematic errors)]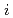 MeV/
MeV/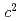 , closer to the
, closer to the 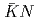 mass threshold than the value determined by the Particle Data Group.
mass threshold than the value determined by the Particle Data Group.
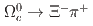 and search for
and search for 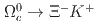 and
and  decays at Belle
decays at BelleHan, X.*; 谷田 聖; Belle Collaboration*; 他170名*
Journal of High Energy Physics (Internet), 2023(1), p.55_1 - 55_12, 2023/01
被引用回数:6 パーセンタイル:57.15(Physics, Particles & Fields)Using a data sample of 980 fb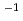 collected with the Belle detector at the KEKB asymmetric-energy
collected with the Belle detector at the KEKB asymmetric-energy 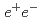 collider, we study for the first time the singly Cabibbo-suppressed decays
collider, we study for the first time the singly Cabibbo-suppressed decays 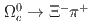 and
and  and the doubly Cabibbo-suppressed decay
and the doubly Cabibbo-suppressed decay 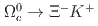 . Evidence for an
. Evidence for an 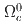 signal in the
signal in the 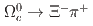 mode is reported with a significance of
mode is reported with a significance of 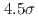 including systematic uncertainties. The ratio of branching fractions to the normalization mode
including systematic uncertainties. The ratio of branching fractions to the normalization mode 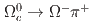 is measured to be
is measured to be 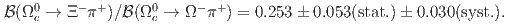 No significant signals of
No significant signals of 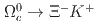 and
and  modes are found. The upper limits at
modes are found. The upper limits at 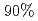 confidence level on ratios of branching fractions are determined to be
confidence level on ratios of branching fractions are determined to be 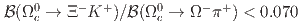 and
and 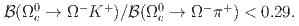
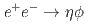 via initial state radiation at Belle
via initial state radiation at BelleZhu, W. J.*; 谷田 聖; Belle Collaboration*; 他174名*
Physical Review D, 107(1), p.012006_1 - 012006_10, 2023/01
被引用回数:2 パーセンタイル:29.46(Astronomy & Astrophysics)Using 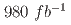 of data collected on and around the
of data collected on and around the 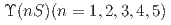 resonances with the Belle detector at the KEKB collider, we measure the cross section of
resonances with the Belle detector at the KEKB collider, we measure the cross section of 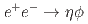 from threshold to
from threshold to 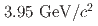 via initial-state radiation. From a multi-parameter fit assuming
via initial-state radiation. From a multi-parameter fit assuming 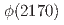 exists in the
exists in the 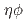 final state according to previous measurement by BESIII, the resonant parameters of
final state according to previous measurement by BESIII, the resonant parameters of 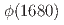 are determined to be
are determined to be 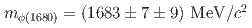 (statistical and systematic errors, respectively),
(statistical and systematic errors, respectively), 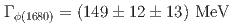 and, depending on the possible presence of interfering resonances,
and, depending on the possible presence of interfering resonances, ![$$Gamma^{e^{+}e^{-}}_{phi(1680)}cdot {cal B}[phi(1680)toetaphi] = (122 pm 6 pm 13)~{rm eV}$$](/search/images/EROEOYLNNVQV241FLZ3SW5LFLZ3S05L3L33VY2DINEUDCNRYGAUX0XDDMRXXIID1LRRWC1BAIJ4VWXDQNBUSQMJWHAYCSXDUN3OGK3DBLRYGQ0K3EA4SAKBRGIZCAXDQNUQDMIC2OBWSAMJTFF5HWXDSNUQGKVT3EQ.gif) ,
,  ,
,  or
or 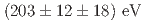 . The branching fraction of
. The branching fraction of 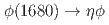 decay is determined to be approximately 20%. Additionally, the branching fraction for
decay is determined to be approximately 20%. Additionally, the branching fraction for 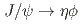 is measured to be
is measured to be 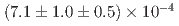 . However, there is no significant observed
. However, there is no significant observed 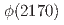 signal in the
signal in the 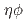 final states in this analysis, and correspondingly the upper limit for
final states in this analysis, and correspondingly the upper limit for 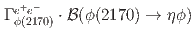 is determined to be either
is determined to be either 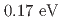 (for two fits), or
(for two fits), or 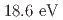 (remaining two fits), at 90% confidence level.
(remaining two fits), at 90% confidence level.
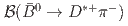 and
and 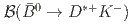 and tests of QCD factorization
and tests of QCD factorizationKrohn, J.-F.*; 谷田 聖; Belle Collaboration*; 他198名*
Physical Review D, 107(1), p.012003_1 - 012003_12, 2023/01
被引用回数:3 パーセンタイル:15.61(Astronomy & Astrophysics)Using 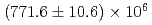
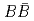 meson pairs recorded by the Belle experiment at the KEKB
meson pairs recorded by the Belle experiment at the KEKB 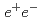 collider, we report the branching fractions
collider, we report the branching fractions 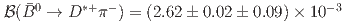 and
and 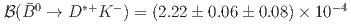 ; the quoted uncertainties are statistical and systematic, respectively. A measurement of the ratio of these branching fractions is also presented,
; the quoted uncertainties are statistical and systematic, respectively. A measurement of the ratio of these branching fractions is also presented, 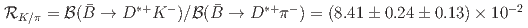 , where systematic uncertainties due to the
, where systematic uncertainties due to the 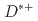 meson reconstruction cancel out. Furthermore, we report a new QCD factorization test based on the measured ratios for
meson reconstruction cancel out. Furthermore, we report a new QCD factorization test based on the measured ratios for 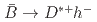 and
and 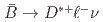 decays at squared momentum transfer values equivalent to the mass of the
decays at squared momentum transfer values equivalent to the mass of the 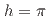 or
or 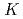 hadron. The parameters
hadron. The parameters 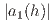 are measured to be
are measured to be 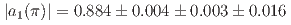 and
and 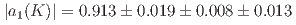 , where the last uncertainties account for all external inputs. These values are approximately
, where the last uncertainties account for all external inputs. These values are approximately 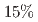 lower than those expected from theoretical predictions. Subsequently, flavor
lower than those expected from theoretical predictions. Subsequently, flavor 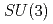 symmetry is tested by measuring the ratios for pions and kaons,
symmetry is tested by measuring the ratios for pions and kaons, 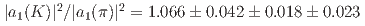 , as well as for different particle species. The ratio is consistent with unity and therefore no evidence for
, as well as for different particle species. The ratio is consistent with unity and therefore no evidence for 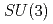 symmetry breaking effects is found at the
symmetry breaking effects is found at the 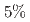 precision level.
precision level.
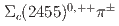
Li, Y. B.*; 谷田 聖; Belle Collaboration*; 他194名*
Physical Review Letters, 130(3), p.031901_1 - 031901_7, 2023/01
被引用回数:16 パーセンタイル:91.49(Physics, Multidisciplinary)We present the study of 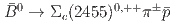 decays based on
decays based on 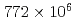
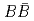 events collected with the Belle detector at the KEKB asymmetric-energy
events collected with the Belle detector at the KEKB asymmetric-energy 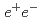 collider. The
collider. The 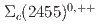 candidates are reconstructed via their decay to
candidates are reconstructed via their decay to 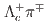 and
and 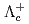 decays to
decays to 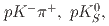 and
and 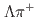 final states. The corresponding branching fractions are measured to be
final states. The corresponding branching fractions are measured to be 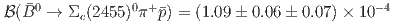 and
and 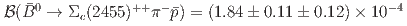 , which are consistent with the world average values with improved precision. A new structure is found in the
, which are consistent with the world average values with improved precision. A new structure is found in the 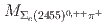 spectrum with a significance of
spectrum with a significance of 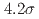 including systematic uncertainty. The structure is possibly an excited
including systematic uncertainty. The structure is possibly an excited 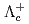 and is tentatively named
and is tentatively named 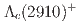 . Its mass and width are measured to be
. Its mass and width are measured to be 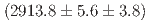 MeV/
MeV/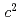 and
and 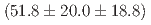 MeV, respectively. The products of branching fractions for the
MeV, respectively. The products of branching fractions for the 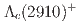 are measured to be
are measured to be 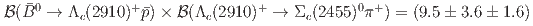 and
and 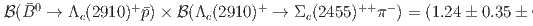 . Here, the first and second uncertainties are statistical and systematic, respectively.
. Here, the first and second uncertainties are statistical and systematic, respectively.
 atoms (J-PARC E03, E07 and future)
atoms (J-PARC E03, E07 and future)山本 剛史; 藤田 真奈美; 後神 利志*; 原田 健志*; 早川 修平*; 細見 健二; 市川 裕大; 石川 勇二*; 鎌田 健人*; 叶内 萌香*; et al.
EPJ Web of Conferences, 271, p.03001_1 - 03001_5, 2022/11
X-ray spectroscopy of hadronic atoms give us various information on the strong interaction between hadrons and nuclei. At J-PARC, we are aiming for the world-first detection of the X rays from atoms with a doubly strange hyperon, 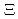
 . Recently, two experiments, J-PARC E07 and J-PARC E03, have been performed for the detection of X rays from
. Recently, two experiments, J-PARC E07 and J-PARC E03, have been performed for the detection of X rays from 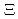
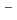 atoms. Overview and status of these measurements will be presented. We will also discuss future plan of X-ray spectroscopy on
atoms. Overview and status of these measurements will be presented. We will also discuss future plan of X-ray spectroscopy on 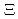
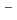 -atoms, which can be performed together with high resolution
-atoms, which can be performed together with high resolution 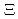
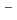 hyper nuclear spectroscopy using newly constructed S-2S spectrometer. Preparation status will be shown in this contribution.
hyper nuclear spectroscopy using newly constructed S-2S spectrometer. Preparation status will be shown in this contribution.
三輪 浩司*; 藤田 真奈美; 原田 健志; 長谷川 勝一; 細見 健二; 市川 真也; 今井 憲一*; 佐甲 博之; 佐藤 進; 田村 裕和; et al.
EPJ Web of Conferences, 271, p.04001_1 - 04001_7, 2022/11
A new hyperon-proton scattering experiment, dubbed J-PARC E40, was performed to measure differential cross sections of the 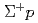 ,
, 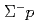 elastic scatterings and the
elastic scatterings and the 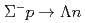 scattering by identifying a lot of
scattering by identifying a lot of 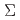 particles in the momentum ranging from 0.4 to 0.8 GeV/
particles in the momentum ranging from 0.4 to 0.8 GeV/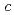 produced by the
produced by the 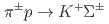 reactions. We successfully measured the differential cross sections of these three channels with a drastically improved accuracy with a fine angular step. These new data will become important experimental constraints to improve the theories of the two-body baryon-baryon interactions. Following this success, we proposed a new experiment to measure the differential cross sections and spin observables by using a highly polarized
reactions. We successfully measured the differential cross sections of these three channels with a drastically improved accuracy with a fine angular step. These new data will become important experimental constraints to improve the theories of the two-body baryon-baryon interactions. Following this success, we proposed a new experiment to measure the differential cross sections and spin observables by using a highly polarized 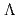 beam for providing quantitative information on the
beam for providing quantitative information on the 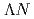 interaction. The results of three
interaction. The results of three 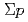 channels and future prospects of the
channels and future prospects of the 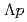 scattering experiment are described.
scattering experiment are described.
佐久間 史典*; 田村 裕和; 谷田 聖; 山本 剛史; 他39名*
EPJ Web of Conferences, 271, p.11001_1 - 11001_7, 2022/11
The J-PARC Hadron Experimental Facility was constructed with an aim to explore the origin and evolution of matter in the universe through experiments with intense particle beams. In the past decade, many results from particle and nuclear physics experiments have been obtained at the present facility. To expand the physics programs to as yet unexplored regions, the extension project of the Hadron Experimental Facility has been extensively discussed. This contribution presents the physics of the extension of the Hadron Experimental Facility to resolve issues related to strangeness nuclear physics, hadron physics, and flavor physics.
後神 利志*; 江端 健悟; 藤田 真奈美; 原田 健志; 長谷川 勝一; 細見 健二; 市川 裕大; 今井 憲一*; Kim, S.; 七村 拓野; et al.
EPJ Web of Conferences, 271, p.11002_1 - 11002_7, 2022/11
In the K1.8 beam-line at Hadron Experimental Facility of J-PARC, a new magnetic spectrometer S-2S is being installed. S-2S was designed to achieve a high momentum resolution of 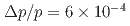 in FWHM. Several strangeness-physics programs which require the high resolution will be realized by S-2S. The present article introduces J-PARC E70 (missing-mass spectroscopy of
in FWHM. Several strangeness-physics programs which require the high resolution will be realized by S-2S. The present article introduces J-PARC E70 (missing-mass spectroscopy of 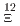 Be) and E94 (missing-mass spectroscopy of
Be) and E94 (missing-mass spectroscopy of 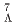 Li,
Li, 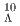 B, and
B, and 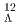 C) experiments.
C) experiments.