Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
目黒 智成*; 小沢 耀弘*; 小林 浩二*; 荒木 康史; 野村 健太郎*
Physical Review Research (Internet), 7(2), p.L022065_1 - L022065_8, 2025/06
We theoretically find a topological spin-orbit torque (SOT) in the compensated ferrimagnetic Weyl semimetal Ti MnAl. The topological SOT arises from all the occupied states, which is free from dissipation. However, it is negligible in metallic magnets and was not reported in Weyl semimetals. We show the enhancement of the topological SOT from the mixed Berry curvature around the Weyl points in Ti
MnAl. The topological SOT arises from all the occupied states, which is free from dissipation. However, it is negligible in metallic magnets and was not reported in Weyl semimetals. We show the enhancement of the topological SOT from the mixed Berry curvature around the Weyl points in Ti MnAl. This finding provides a guiding principle for designing highly efficient SOT devices using the topological nature of ferrimagnetic Weyl semimetals.
MnAl. This finding provides a guiding principle for designing highly efficient SOT devices using the topological nature of ferrimagnetic Weyl semimetals.
小沢 耀弘*; 荒木 康史; 野村 健太郎*
Journal of the Physical Society of Japan, 93(9), p.094704_1 - 094704_9, 2024/09
被引用回数:0 パーセンタイル:0.00(Physics, Multidisciplinary)磁性ワイル半金属における磁化の変調は、運動量空間におけるワイル点位置のシフトを引き起こし、ワイルフェルミオンに対して実効的なカイラリティ依存のゲージ場として働く。本研究では、完全スピン偏極したワイル強磁性体Co Sn
Sn S
S において、このような磁化誘起カイラルゲージ場の効果を取り扱う。磁化と結合した積層カゴメ格子上で定義したCo
において、このような磁化誘起カイラルゲージ場の効果を取り扱う。磁化と結合した積層カゴメ格子上で定義したCo Sn
Sn S
S の強束縛模型を用いて、運動量空間におけるワイル点の位置(カイラルゲージ場に相当)の磁化方向依存性を計算した。これを用いて、磁壁構造が存在する場合に、カイラルゲージ場の空間構造から生じるカイラル磁場を評価した。その結果磁壁存在下では、ワイルフェルミオンに対してランダウ量子化を強く引き起こすほどの、数百テスラという巨大なカイラル磁場が生じることが導出された。このような巨大カイラル磁場は、従来の磁性体スピントロニクスにおけるスピン起電力に相当する、磁壁の運動による電荷ポンピングを誘起することも予想される。
の強束縛模型を用いて、運動量空間におけるワイル点の位置(カイラルゲージ場に相当)の磁化方向依存性を計算した。これを用いて、磁壁構造が存在する場合に、カイラルゲージ場の空間構造から生じるカイラル磁場を評価した。その結果磁壁存在下では、ワイルフェルミオンに対してランダウ量子化を強く引き起こすほどの、数百テスラという巨大なカイラル磁場が生じることが導出された。このような巨大カイラル磁場は、従来の磁性体スピントロニクスにおけるスピン起電力に相当する、磁壁の運動による電荷ポンピングを誘起することも予想される。
 Sn
Sn S
S -based shandite films
-based shandite filmsLau, Y.-C.*; 池田 絢哉*; 藤原 宏平*; 小沢 耀弘*; Zheng, J.*; 関 剛斎*; 野村 健太郎*; Du, L.*; Wu, Q.*; 塚崎 敦*; et al.
Physical Review B, 108(6), p.064429_1 - 064429_11, 2023/08
被引用回数:11 パーセンタイル:72.60(Materials Science, Multidisciplinary)Magnetic Weyl semimetals (mWSMs) are characterized by linearly dispersive bands with chiral Weyl node pairs associated with broken time-reversal symmetry. One of the hallmarks of mWSMs is the emergence of large intrinsic anomalous Hall effect. On heating the mWSM above its Curie temperature, the magnetism vanishes while exchange-split Weyl point pairs collapse into doubly degenerate gapped Dirac states. Here, we reveal the attractive potential of these Dirac nodes in paramagnetic state for efficient spin current generation at room temperature via the spin Hall effect. Ni and In are introduced to separately substitute Co and Sn in a prototypal mWSM Co Sn
Sn S
S shandite film and tune the Fermi level. Composition dependence of spin Hall conductivity for paramagnetic shandite at room temperature resembles that of anomalous Hall conductivity for ferromagnetic shandite at low temperature; exhibiting peak-like dependence centering around the Ni-substituted Co
shandite film and tune the Fermi level. Composition dependence of spin Hall conductivity for paramagnetic shandite at room temperature resembles that of anomalous Hall conductivity for ferromagnetic shandite at low temperature; exhibiting peak-like dependence centering around the Ni-substituted Co Ni
Ni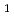 Sn
Sn S
S and undoped Co
and undoped Co Sn
Sn S
S compositions, respectively. The observed spin Hall and anomalous Hall conductivity maxima at different compositions reflect optimum Fermi-level positioning relative to the paramagnetic Dirac and magnetic Weyl states, suggesting the common origin and intercorrelation between the two Hall effects. Our findings highlight a strategy for the quest of spin Hall materials, guided by the abundant experimental anomalous Hall-effect data of ferromagnets in the literature.
compositions, respectively. The observed spin Hall and anomalous Hall conductivity maxima at different compositions reflect optimum Fermi-level positioning relative to the paramagnetic Dirac and magnetic Weyl states, suggesting the common origin and intercorrelation between the two Hall effects. Our findings highlight a strategy for the quest of spin Hall materials, guided by the abundant experimental anomalous Hall-effect data of ferromagnets in the literature.
渡邊 成*; 荒木 康史; 小林 浩二*; 小澤 耀弘*; 野村 健太郎*
Journal of the Physical Society of Japan, 91(8), p.083702_1 - 083702_5, 2022/08
被引用回数:7 パーセンタイル:63.47(Physics, Multidisciplinary)本論文では籠目格子上で構成される磁気秩序について、電子系の強束縛ハミルトニアンに基づいて数値計算を行い、電子の充填率及びスピン軌道相互作用の強さに対する依存性を調べる。籠目格子上では電子の充填率によって、強磁性及びノンコリニア反強磁性秩序のいずれも取りうることを示す。これらの磁気秩序は、籠目格子に特有のディラック分散や平坦バンドといったバンド構造に由来するものである。更に、Kane-Mele型やRashba型のスピン軌道相互作用を導入することで、実効的なDzyaloshinskii-Moriya相互作用が誘起され、磁気スパイラルや反強磁性120度構造等のノンコリニアな磁気秩序が安定化されることを示す。本研究によって得られた磁気秩序の相構造に関する知見は、ワイル・ディラック電子を示すような籠目格子の層状物質群における磁気秩序の起源を理解するのに役立つと期待される。
荒木 康史; 渡邊 成*; 野村 健太郎*
Journal of the Physical Society of Japan, 90(9), p.094702_1 - 094702_9, 2021/09
被引用回数:1 パーセンタイル:11.54(Physics, Multidisciplinary)磁性を持つ線ノード半金属はいくつかの化合物で理論的および実験的に確認されているが、一方で、その磁気秩序と電子の性質の間の関係性についての理解は進んでいない。本研究では磁性線ノード半金属のバルク及び境界面における電子の性質を理解することを目的として、トポロジカルディラック半金属(TDSM)に磁性を導入した系を数値的および解析的に取り扱う。TDSMはスピン縮退したディラック点のペアを持つ物質であり、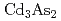 及び
及び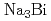 等が知られている。TDSMの格子模型で電子スピンに結合した磁化を導入してバンド構造を計算することにより、TDSMは磁化の向き及び結合定数に依存して、ワイル半金属または線ノード半金属のいずれかに転移することが示された。これによって得られた磁性線ノード半金属相の電子状態を計算することにより、境界面においては線ノードに対応したドラムヘッド型バンド構造を持つゼロモードが現れることが示された。この境界モードはバルクの整数
等が知られている。TDSMの格子模型で電子スピンに結合した磁化を導入してバンド構造を計算することにより、TDSMは磁化の向き及び結合定数に依存して、ワイル半金属または線ノード半金属のいずれかに転移することが示された。これによって得られた磁性線ノード半金属相の電子状態を計算することにより、境界面においては線ノードに対応したドラムヘッド型バンド構造を持つゼロモードが現れることが示された。この境界モードはバルクの整数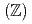 トポロジカル数により特徴づけられるものであり、磁壁に局在して現れることが見出された。
トポロジカル数により特徴づけられるものであり、磁壁に局在して現れることが見出された。
紅林 大地*; 荒木 康史; 野村 健太郎*
Journal of the Physical Society of Japan, 90(8), p.084702_1 - 084702_9, 2021/08
被引用回数:9 パーセンタイル:57.92(Physics, Multidisciplinary)本研究では、磁性ワイル半金属において電流および電圧によって誘起されるスピントルクの理論を導出する。磁性ワイル半金属においては、非自明なトポロジーを持つバンド構造に由来して磁化と電子輸送が結合し、スピントロニクスに適した性質を示す。本論文では、磁化構造の勾配および電流に関する摂動展開に基づき、電流によって誘起されるスピントルクを網羅的に導出する。このトルクはスピン軌道トルク及びスピン移行トルクを内包するものである。更に、電圧(電位差)によって誘起されるトルクも微視的に導出し、このトルクがスピンと軸性カレントの対応関係、及びカイラルアノマリーに由来するものであることを示す。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
Physical Review Research (Internet), 3(2), p.023219_1 - 023219_15, 2021/06
本論文では、トポロジカルディラック半金属(TDSM)表面のギャップレス状態を介した、長距離スピン伝送を理論面から提案する。次世代のスピントロニクス素子の構築のためには、散逸の少ないスピン流を実現することが必要である。主要なスピン流のキャリアは金属中の伝導電子や磁性絶縁体中のスピン波であるが、これらはジュール熱やギルバート緩和により伝播距離が制限される問題がある。本研究ではTDSM(Cd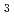 As
As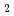 , Na
, Na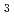 Bi等)のスピン・ヘリカルな表面状態が、乱れに対して頑強である性質を用いて、低散逸で長距離のスピン輸送を提案する。2つの磁性絶縁体とTDSMの接合系を考え、一方の磁性体の磁化ダイナミクスにより、TDSM表面を介して他方の磁性体に注入されるスピン流に注目する。表面における輸送理論と、格子模型による実時間発展シミュレーションを併用することにより、TDSM表面を流れるスピン流は準量子化された値をとり、その値は界面の微視的な結合の構造によらないことを示す。さらに、このスピン流は長距離においても乱れに対して強いことを示し、TDSMがスピントロニクス素子へ応用可能な表面状態をもつことを提案する。
Bi等)のスピン・ヘリカルな表面状態が、乱れに対して頑強である性質を用いて、低散逸で長距離のスピン輸送を提案する。2つの磁性絶縁体とTDSMの接合系を考え、一方の磁性体の磁化ダイナミクスにより、TDSM表面を介して他方の磁性体に注入されるスピン流に注目する。表面における輸送理論と、格子模型による実時間発展シミュレーションを併用することにより、TDSM表面を流れるスピン流は準量子化された値をとり、その値は界面の微視的な結合の構造によらないことを示す。さらに、このスピン流は長距離においても乱れに対して強いことを示し、TDSMがスピントロニクス素子へ応用可能な表面状態をもつことを提案する。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
Physical Review Research (Internet), 2(2), p.023195_1 - 023195_11, 2020/05
We theoretically manifest that the edge of a quantum spin Hall insulator (QSHI), attached to an insulating ferromagnet (FM), can realize a highly efficient spin-to-charge conversion. Based on a one-dimensional QSHI-FM junction, the electron dynamics on the QSHI edge is analyzed, driven by a magnetization dynamics in the FM. Under a large gap opening on the edge from the magnetic exchange coupling, we find that the spin injection into the QSHI edge gets suppressed while the charge current driven on the edge gets maximized, demanded by the band topology of the one-dimensional helical edge states.
塩見 雄毅*; 野村 健太郎*; 梶原 瑛祐*; 江藤 数馬*; Novak, M.*; 瀬川 耕司*; 安藤 陽一*; 齊藤 英治
Physical Review Letters, 113(19), p.196601_1 - 196601_5, 2014/11
被引用回数:298 パーセンタイル:98.98(Physics, Multidisciplinary)We report successful spin injection into the surface states of topological insulators by using a spin pumping technique. By measuring the voltage that shows up across the samples as a result of spin pumping, we demonstrate that a spin-electricity conversion effect takes place in the surface states of bulk-insulating topological insulators Bi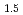 Sb
Sb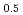 Te
Te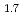 Se
Se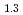 and Sn-doped Bi
and Sn-doped Bi Te
Te Se. In this process, the injected spins are converted into a charge current along the Hall direction due to the spin-momentum locking on the surface state.
Se. In this process, the injected spins are converted into a charge current along the Hall direction due to the spin-momentum locking on the surface state.
 の溶解挙動評価試験
の溶解挙動評価試験佐野 雄一; 新井 健太郎*; 桜井 孝二*; 柴田 淳広; 野村 和則; 青嶋 厚*
JNC TN8400 2000-032, 98 Pages, 2000/12
再処理プロセスへの晶析工程の導入時に必要となる高濃度U溶液の調製、さらにはその際の有効な手法の一つである粉体化燃料を対称とした溶解に関連し、U濃度が最大800g/Lまでの領域におけるUO2粉末の溶解挙動を明らかとすることを目的として、溶解挙動に及ぼす最終U濃度、溶解温度、初期硝酸濃度、粉末粒径及び燃料形態の影響について評価を行った。また、得られた結果をもとに高濃度溶解時における照射済MOX燃料の溶解挙動について評価を行い、晶析工程への高HM濃度溶液供給の可能性について検討を行った。試験の結果、最終U濃度、粉末粒径の増大及び溶解温度、初期硝酸濃度の減少に伴う溶解性の低下が認められた。さらに、UO 粉末及びUO
粉末及びUO ペレットの高濃度溶解時においても、最終U濃度が溶解度に対して十分低い(U濃度/溶解度
ペレットの高濃度溶解時においても、最終U濃度が溶解度に対して十分低い(U濃度/溶解度 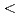 約0.8)溶解条件下では、fragmentationモデルに基づいた既報の評価式によりその溶解挙動の予測が可能であることを確認した。晶析工程への高HM濃度溶液(500g/L
約0.8)溶解条件下では、fragmentationモデルに基づいた既報の評価式によりその溶解挙動の予測が可能であることを確認した。晶析工程への高HM濃度溶液(500g/L )供給の可能性については、従来の燃料剪断片を用いた溶解では、高HM濃度の溶液を得ることが困難(溶解時間が大幅に増加する)であるが、燃料を粉体化することにより速やかに高HM濃度溶液を得ることができるとの見通しを得た。粉体化した燃料の溶解時に懸念される溶解初期のオフガスの急激な発生は溶解条件を考慮することによりある程度回避できるものと考えられ、今後オスガス処理工程の最大処理能力を踏まえた上で溶解条件の最適化を進めることが重要となる。
)供給の可能性については、従来の燃料剪断片を用いた溶解では、高HM濃度の溶液を得ることが困難(溶解時間が大幅に増加する)であるが、燃料を粉体化することにより速やかに高HM濃度溶液を得ることができるとの見通しを得た。粉体化した燃料の溶解時に懸念される溶解初期のオフガスの急激な発生は溶解条件を考慮することによりある程度回避できるものと考えられ、今後オスガス処理工程の最大処理能力を踏まえた上で溶解条件の最適化を進めることが重要となる。
小沢 耀弘*; 荒木 康史; 野村 健太郎*
no journal, ,
We show our recent theoretical analysis of the structure of the chiral gauge field in a ferromagnetic Weyl semimetal with magnetic domain walls. We focus on Co Sn
Sn S
S , which is one of the representative systems for magnetic Weyl semimetals. This system exhibits nearly full spin polarization due to the large spin splitting by ferromagnetic ordering. Based on an effective tight-binding model of Co
, which is one of the representative systems for magnetic Weyl semimetals. This system exhibits nearly full spin polarization due to the large spin splitting by ferromagnetic ordering. Based on an effective tight-binding model of Co Sn
Sn S
S , we study the relation between the shift of Weyl points in momentum space and the direction of the magnetization. With this result, we show the spatial structure and magnitude of the chiral gauge field, when the domain wall is formed in Co
, we study the relation between the shift of Weyl points in momentum space and the direction of the magnetization. With this result, we show the spatial structure and magnitude of the chiral gauge field, when the domain wall is formed in Co Sn
Sn S
S . With this chiral gauge field picture, we propose that the domain wall dynamics drive a sizable electric current, which arises as the Hall current under the chiral electromagnetic fields. This current may be useful for detecting the domain wall dynamics, in future spintronic devices based on magnetic Weyl semimetals.
. With this chiral gauge field picture, we propose that the domain wall dynamics drive a sizable electric current, which arises as the Hall current under the chiral electromagnetic fields. This current may be useful for detecting the domain wall dynamics, in future spintronic devices based on magnetic Weyl semimetals.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on spin pumping into a two-dimensional (2D) quantum spin Hall inslator (QSHI). QSHI is a topological insulator in 2D exhibiting gapless helical edge stats, which are responsible for the quantized spin Hall conductivity. Recent theories and experiments have demonstrated the QSHI phase in a monolayer of transition metal dichalcogenide 1T'-WTe2, which can be easily engineered in contrast to traditionally-known HgTe/CdTe and InAs/GaSb quantum wells. While the theory of spin pumping is well established in normal metals by focusing on the spin-dependent electron scattering at the interface, it is unreliable for topologically nontrivial interfaces in such systems. In the present work, we consider a junction of a ferromagnet and a 2D QSHI at its 1D edge, and demonstrate the pumping of angular momentum from the spin-precessing ferromagnet into the QSHI. Using the Floquet theory for the electrons on the helical edge states, we analytically show that the time-periodic precession of the magnetization drives a charge current on the edge, for the whole range of precession frequency. This edge current can be regarded as a consequence of the inverse spin Hall effect intrinsic to the QSHI, which converts the injected spin current into a transverse charge current. By varying the precession frequency of the magnetization and the coupling strength at the junction, we find a clear crossover between two regimes: the adiabatic regime, where the slow magnetization precession drives a quantized pumping, and the resonant regime, where the fast precession leads to a suppressed pumping. We also incorporate the effect of orbital dependence in the exchange coupling at the edge, and show numerically that it shifts the crossover point between the adiabatic and resonant regimes.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on spin pumping into a two-dimensional (2D) quantum spin Hall inslator (QSHI). Recent theories and experiments have demonstrated the QSHI phase in a monolayer of transition metal dichalcogenide 1T'-WTe2, which can be easily engineered in contrast to traditionally-known HgTe/CdTe and InAs/GaSb quantum wells. While the theory of spin pumping is well established in normal metals by focusing on the spin-dependent electron scattering at the interface, it is unreliable for topologically nontrivial interfaces in such systems. In the present work, we consider a junction of a ferromagnet and a 2D QSHI at its 1D edge, and demonstrate the pumping of angular momentum from the spin-precessing ferromagnet into the QSHI. Using the Floquet theory for the electrons on the helical edge states, we analytically show that the time-periodic precession of the magnetization drives a charge current on the edge, for the whole range of precession frequency. This edge current can be regarded as a consequence of the inverse spin Hall effect intrinsic to the QSHI, which converts the injected spin current into a transverse charge current. By varying the precession frequency of the magnetization and the coupling strength at the junction, we find a clear crossover between two regimes: the adiabatic regime, where the slow magnetization precession drives a quantized pumping, and the resonant regime, where the fast precession leads to a suppressed pumping. We also incorporate the effect of orbital dependence in the exchange coupling at the edge, and show numerically that it shifts the crossover point between the adiabatic and resonant regimes.
小沢 耀弘*; 荒木 康史; 野村 健太郎*
no journal, ,
ワイルフェルミオンは、相対論的場の量子論おいて導入される無質量のフェルミオンである。カイラリティー自由度は、ワイル粒子のスピン方向が運動量方向に対して並行(左巻き)か反並行(右巻き)かを区別する量である。異なるカイラリティーを持つワイル粒子に対して逆向きに結合するカイラルゲージ場は、カイラリティの保存則を破る量子異常に寄与する。カイラルゲージ場は相対論的場の理論で導入される仮想的な自由度であるが、ワイル半金属と呼ばれる量子物質においてその効果が実現することが期待されている。ワイル半金属においては、ワイルフェルミオンはギャップレス点であるワイル点近傍の低エネルギー励起として現れる(ワイル電子)。このワイル点がある摂動によって移動したとき、そのずれはカイラルゲージ場とみなせる。物質系でカイラルゲージ場を実現する効果として、格子歪みや円偏光などが調べられている。中でも、磁気秩序を持つワイル半金属(磁性ワイル半金属)においては、磁気モーメントがカイラルゲージ場としてはたらく。このため、磁壁駆動に代表される磁化ダイナミクスが、ワイル電子のトポロジカルな性質を通して駆動できることが期待される。本講演では、磁性ワイル半金属における磁気構造に起因したカイラルゲージ場の理論解析を紹介する。特に、典型的な強磁性ワイル半金属であるCo Sn
Sn S
S に注目する。Co
に注目する。Co Sn
Sn S
S の低エネルギー電子状態を記述する有効模型を用いて、磁気モーメント方向に対してどのようにワイル点が移動するのかを示す。その結果に基づき、磁壁構造が存在する場合にカイラルゲージ場がどのような空間構造を持つのかを議論する。さらに、カイラルゲージ場から導出される有効電磁場の描像を用いて、Co
の低エネルギー電子状態を記述する有効模型を用いて、磁気モーメント方向に対してどのようにワイル点が移動するのかを示す。その結果に基づき、磁壁構造が存在する場合にカイラルゲージ場がどのような空間構造を持つのかを議論する。さらに、カイラルゲージ場から導出される有効電磁場の描像を用いて、Co Sn
Sn S
S における磁壁駆動の観測方法を提案する。
における磁壁駆動の観測方法を提案する。
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
The two-dimensional quantum spin Hall insulator (2D QSHI) is the most primitive but quite important realization of topological insulator. It shows the helical edge states protected by time-reversal symmetry, whereas the quantized spin Hall conductivity in the bulk. In the present work, we theoretically investigate the spin pumping from a precessing ferromagnet into a 2D QSHI thoroughly from the adiabatic to nonadiabatic regimes, both analytically and numerically. We analytically treat the dynamics of the edge-state electrons coupled to the precessing ferromagnet by the Floquet theory, and derive the pumped current as a function of the exchange energy and the precession frequency. We find that a heat bath for the edge electrons governs the transition between the adiabatic and nonadiabatic regime: when the edge electrons are coupled with a heat bath, their spin and energy can dissipate into the bath by a certain rate, eventually reaching a periodic steady state. The pumped current on the becomes quantized when the exchange energy exceeds the dissipation rate. We also calculate the edge current numerically on the 2D lattice model, and find that the bulk states in the QSHI effectively serves as the heat bath for the edge electrons.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
We present our theoretical work on dynamical spin-to-charge conversion at the edge of a quantum spin Hall insulator (QSHI), namely a two-dimensional topological insulator with helical edge states. Interconversion between spin- and charge-related quantities has been a key idea in making use of magnetic materials, especially in the context of spintronics. QSHI is a typical system showing a universal charge-to-spin conversion behavior, namely the quantum spin Hall effect, whereas the spin-to-charge conversion therein is still not clearly understood. At a lateral heterojunction of a ferromagnet (FM) and a QSHI, it has been theoretically demonstrated that magnetization dynamics induces a charge current along the edge of QSHI; however, its mechanism from the viewpoint of spin-to-charge conversion still remains to be clarified. In order to understand the spin transfer and the spin-to-charge conversion mechanism in QSHI, we investigate the many-body dynamics of the electrons under the magnetization dynamics at the QSHI-FM junction. We analytically treat the electron dynamics in terms of the Floquet-Keldysh formalism, and compare two physical quantities present on the edge: the spin injection rate from the FM into the QSHI, and the charge current induced along the edge. Whereas the edge current seen in the previous works is reproduced, we find that it is not proportional to the spin injection rate, especially when the exchange interaction at the junction is strong enough. This relation implies that the spin-to-charge conversion in this system cannot be considered as the inverse spin Hall effect, while it can be rather seen as the inverse Edelstein effect, in which an electron spin accumulation at the junction is converted to a charge current. We also focus on the energy transfer at the junction, and interpret this phenomenon in terms of magnon exchange.
荒木 康史; 三澤 貴宏*; 野村 健太郎*
no journal, ,
Cd As
As 等のトポロジカルディラック半金属の表面には、フェルミアークとしてスピンヘリカルな1次元的状態が存在する。本講演ではこの表面状態を介したスピン輸送について議論する。半金属表面に2つの磁性絶縁体が接合した状況を考え、片方の磁性体の磁化ダイナミクスが、半金属表面状態を介して他方の磁性体に与えるスピン流を扱う。このスピン流がフェルミアークの長さに応じた量子化値をとることを、解析的および数値的に示す。
等のトポロジカルディラック半金属の表面には、フェルミアークとしてスピンヘリカルな1次元的状態が存在する。本講演ではこの表面状態を介したスピン輸送について議論する。半金属表面に2つの磁性絶縁体が接合した状況を考え、片方の磁性体の磁化ダイナミクスが、半金属表面状態を介して他方の磁性体に与えるスピン流を扱う。このスピン流がフェルミアークの長さに応じた量子化値をとることを、解析的および数値的に示す。
渡邊 成*; 荒木 康史; 野村 健太郎*
no journal, ,
本研究ではカゴメ電子系のハミルトニアンが持つ微視的性質から、スピン系の巨視的な磁気秩序の性質を導くことを目標に研究を行なった。具体的にはRashba型、及びKane-Mele型のスピン軌道相互作用が存在する単層カゴメ格子上の電子系から出発し、種々の磁気構造における電子系のエネルギーを計算した。これにより基底状態として実現する磁気構造の相図を得た。これによりnoncollinearな磁気秩序が基底状態となることを明らかにした。さらに古典的Heisenberg模型を用いて、スピン間相互作用とジャロシンスキー・守谷相互作用の、電子系のパラメーター依存性を導くことで、古典的Heisenberg模型で記述されるスピン系の巨視的性質を電子系の微視的性質から導いた。