Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
板垣 正文; C.A.Brebbia*
境界要素法研究会BEM・テクノロジー・コンファレンス論文集, p.59 - 64, 1993/06
中性子拡散方程式はHelmholtz方程式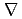
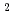
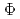 +B
+B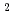
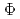 =0の一種である。この式を
=0の一種である。この式を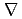
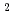
 +Bo
+Bo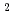
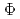 +
+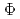 /
/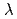 =0のように変形する。ここにBo
=0のように変形する。ここにBo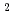 はB
はB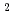 の推定値である。
の推定値である。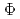 /
/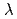 をソース項とみなせば、
をソース項とみなせば、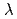 の値を探索するのに原子炉解析で広く用いられているソース反復の手法が使える。2次元問題に対する境界積分方程式が、複素関数であるHankel関数に基づく基本解を使って導かれる。多重相反法を適用することにより、上記ソース項に起因する領域積分が境界積分のみの級数に変換される。また、固有値B
の値を探索するのに原子炉解析で広く用いられているソース反復の手法が使える。2次元問題に対する境界積分方程式が、複素関数であるHankel関数に基づく基本解を使って導かれる。多重相反法を適用することにより、上記ソース項に起因する領域積分が境界積分のみの級数に変換される。また、固有値B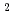 も二つの境界積分の比として与えられ、多重相反境界要素法による固有値探索の過程では、領域内部に関しての情報が一切不要となる。多重相反計算の収束安定性について考慮が加えられ、Bo
も二つの境界積分の比として与えられ、多重相反境界要素法による固有値探索の過程では、領域内部に関しての情報が一切不要となる。多重相反計算の収束安定性について考慮が加えられ、Bo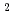
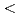 B
B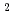 /2を満たすように推定値Bo
/2を満たすように推定値Bo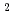 選ぶと安定な収束を保証できることが判った。
選ぶと安定な収束を保証できることが判った。
板垣 正文; C.A.Brebbia*
Boundary Element Methods, p.79 - 88, 1993/00
ここで提案する方法では、通常のHelmholtz方程式を源項を持つ方程式に変形し、源項反復によって固有値を求める。これを境界要素法で解こうとする時、源項に起因する領域積分が生じるが、多重相反法を適用して等価な境界積分に変換できる。固有値自身も二つの境界積分を用いて表わされる。従来、この種の問題を解くのには行列式サーチが多く用いられていたが、数値的に不安定で大規模な問題に対しては取扱いが困難であった。提案する方法は原子炉解析で中性子源反復法として実績のある源項反復法に基づいていることから安定な収束が得られる。二次元の計算例に対する結果から、この方法による固有値探索は収束が極めて早く、Helmholtz型固有値問題の解法に有効であることが示された。原子炉の臨界解析のみならず、音響、振動、波動等、Helmholtz方程式で記述される多くの工学問題に適用可能である。
板垣 正文; C.A.Brebbia*
Engineering Analysis with Boundary Elements,11, p.87 - 90, 1993/00
2次元修正ヘルムホルツ方程式で記述される物理現象を多重相反境界要素法で解く際に必要となる高次基本解を導いた。(L-1)次の基本解をソース項にもつ方程式の第L次基本解は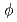
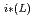 =A
=A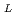 (kr)
(kr)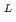 K
K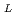 (kr)の形式をしている。ここにK
(kr)の形式をしている。ここにK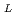 (-)は第L次の変形ベッセル関数であり、係数A
(-)は第L次の変形ベッセル関数であり、係数A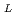 はA
はA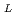 =A
=A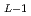 /(2Lk
/(2Lk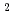 )で与えられて、初期値はA
)で与えられて、初期値はA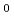 =1/(2
=1/(2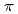 )である。第L次基本解でこのように表わされることが示される。本報で示される高次基本解導出のプロセスは他の工学問題の微分方程式においても応用し得るものである。なお、修正ヘルムホルツ方程式は、そのまま中性子拡散方程式と同一型式であることが知られており、原子炉解析への応用が考えられる。
)である。第L次基本解でこのように表わされることが示される。本報で示される高次基本解導出のプロセスは他の工学問題の微分方程式においても応用し得るものである。なお、修正ヘルムホルツ方程式は、そのまま中性子拡散方程式と同一型式であることが知られており、原子炉解析への応用が考えられる。
板垣 正文; C.A.Brebbia*
Engineering Analysis with Boundary Elements,11, p.39 - 45, 1993/00
エネルギー1群の核分裂中性子源反復計算を境界要素法で実行する際に多重相反法(MRM:Multiple Reciprocity Method)をあてはめた定式化を試みた。第m回目の中性子源反復において核分裂中性子源に関わる領域積分が、多重相反定理の活用により、(m-1)個の境界積分に変換される。この境界積分の実行には零次から(m-1)次の高次基本解が必要であり、2次元問題では高次の変形ベッセル関数を使って記述される。またこの境界積分では、過去の中性子源反復で計算された境界上の中性子束及び中性子流を保存しておく必要がある。ここで示された定式化は2次元問題と3次元問題の両方に適用可能である。この定式化に基づく計算コードが実用になれば、領域内部の情報は全く不必要になり、境界のみを離散化すれば良いことになるので、境界要素法が持つ本来の利点が最大限に活かされることになる。
板垣 正文; C.A.Brebbia*
Boundary Elem. Abstr. Newsl., 3(2), p.67 - 70, 1992/03
中性子源反復計算を多重相反境界要素法を用いて試みた。この方法の利点は、問題とする領域の内部をメッシュ分割する必要がなく、境界のみを離散化して境界要素を定義するのみで良いことである。また、不規則な幾何形状を容易に扱えることも利点であり、将来の炉物理解析の自由度を格段に高める潜在的可能性を有している。解析解が得られている簡単な2次元1領域問題を例題として、中性子源反復の進行によって実効増倍率がどのように収束していくかを調べた。反復過程の早い時期に実効増倍率は真値に極めて近づくが、その後、徐々に真値より離れていく現象がみられた。これは、第m回の反復において最高(m-1)次の高次基本解が使われており、まるめの誤差が蓄積したためと考えられる。まるめ誤差の蓄積は、ある条件式に数値をあてはめた時に1を超えた場合に顕著となることが明らかとなった。
板垣 正文; C.A.Brebbia*
Boundary Elements XIV, Vol.1; Field Problems and Applications, p.25 - 38, 1992/00
境界要素法を臨界計算に適用した場合に現れる領域積分項を境界積分に変換する二つの方法、二重相反法と多重相反法について記述する。二重相反法では、核分裂ソース分布をフーリエ級数に展開し、個々の展開項をソースとする拡散方程式の特解を利用して領域積分を等価な境界積分に変換する。必要な展開係数は別の境界積分により自動的に与えられる。多重相反法では中性子源反復の回数に応じた次数の高次基本解を用いて相反定理を繰り返し適用して境界積分のみによる定式化を行う。この方法では境界上の中性子束と中性子流を反復の度に記憶する必要があるが、精度の高い結果が得られやすい。二つの方法とも、本来、中性子束の領域積分の比で与えられる実効増倍率を境界積分のみによる表示とし、計算の効率化を図った。簡単な数値計算例について両者の得失を議論すると共に、今後の開発課題についても触れる。
板垣 正文; C.A.Brebbia*
Engineering Analysis with Boundary Elements, 10, p.345 - 352, 1992/00
被引用回数:9 パーセンタイル:73.00(Engineering, Multidisciplinary)多重相反境界要素法を用いて中性子源反復計算を行う時、ある収束条件が満足されないとまるめ誤差が蓄積していく現象がみられる。この論文はこの数値誤差を除去できる多重相反法の新しい定式化を提案する。上記の収束条件が常に満足されるように中性子拡散方程式をWielandtの原点移動法の考え方に沿って変更する。この場合、境界積分方程式の組立に必要な基本解は、従来法では修正Helmholtz方程式での基本解であったのに対し新しい方法では標準のHelmholtz方程式に対するものとなる。この点を除けば境界積分方程式の型式は新旧で同一である。テスト計算の結果新しい方法によると中性子源反復は急速かつ安定に収束しまるめ誤差の蓄積に伴う数値的不安定現象はもはや見られなくなった。
板垣 正文; C.A.Brebbia*
Engineering Analysis with Boundary Elements, 8(5), p.239 - 244, 1991/10
被引用回数:9 パーセンタイル:76.22(Engineering, Multidisciplinary)近年着目されている数値解法である境界要素法を中性子拡散方程式にそのまま適用すると核分裂中性子源に関する項は領域積分となり、境界要素法の利点が十分に活かされない。本論文では、このような領域積分を等価な境界積分に変換する一般的手法を与えている。まず、実効増倍率は境界上の中性子束と中性子流のみを境界積分することで求められる。核分裂中性子源と基本解の積を核とする領域積分は、核分裂中性子源分布をフーリエ級数に展開することによって等価な境界積分に変換できる。この際に必要となるフーリエ展開係数は同じく境界積分で与えられるが、中性子源反復過程では前回の反復で得られた展開係数を使った漸化式の形式で与えられるので、効率的に反復計算を進めることができる。
板垣 正文; C.A.Brebbia*
Nuclear Science and Engineering, 107, p.246 - 264, 1991/03
被引用回数:15 パーセンタイル:81.63(Nuclear Science & Technology)加圧水型原子炉の炉心-反射体境界またはバッフル板表面に設定するエネルギー依存行列形式の境界条件を計算する目的で境界要素法を用いた。この方法を用いると、内側に凸のL字形境界のみならず、従来解析の困難であった外側に凸のL字形境界も含むあらゆね幾何形状の境界を一回の計算で処理可能となる。さらに、この方法はエネルギーが3群以上であっても適用でき、バッフル板のある反射体も無い反射体も扱うことができる。エネルギー2群など3群からなるいくつかのテスト計算では、この境界条件計算によって得た反射体境界条件を設定した有限差分計算結果は反射体も含めて行なった基準計算結果と較べて高い精度で実効増倍率及び中性子束分布を再現できることが示された。
板垣 正文; C.A.Brebbia*
Boundary Elements XII, Vol.1; Applications in Stress Analysis, Potential and Diffusion, p.227 - 239, 1990/00
中性子拡散問題で遭遇する二領域に挟まれた薄い帯状域を解析する為に従来よりも効率的な境界要素解法を提案する。帯状域の両表面における中性子束と中性子流とを関係づける解析表示が1次元中性子拡散理論から導出される。中性子束と中性子流の連続条件を用いると、帯状域に隣接する二領域の各々に対して設定した境界積分方程式の離散表示は上記の解析表示を介して結合されることができる。即ち、二つの領域と帯状域の組合わせから成る全体系がただひとつの行列方程式によって記述される。この場合、従来の境界要素法では帯状域表面の中性子束と中性子流の全てが未知数として定義する必要があったのに対し、本方法では帯状域に対して要求される未知数の数が半分に減らされている。このような解析モデルの簡素化にもかかわらず、中性子束分布の計算結果は十分精度の高いものであった。この方法の活用により境界要素法の応用範囲が増大する。
板垣 正文; 藤又 康*; C.A.Brebbia*
境界要素法研究会第25回例会研究発表資料, p.1 - 17, 1989/03
近年種々の工学分野で研究されている新しい数値解法である境界要素法を中性子拡散問題に応用すべく行ってきたこれまでの研究の成果とレビューする。グリーンの第2積分公式を用いると中性子拡散方程式は中性子源項を除いて境界積分のみで表わされ、数値計算上多くの利点をもたらす。中性子源項は一般に領域積分となるが、一様中性子源、減速中性子源についてはこれを等価な境界積分に変換する技法が既に確立されている。核分裂中性子源を境界積分で表わす手法の研究開発は過去1年間で急速に進展しフーリエ級数展開を採用することが有用であることを明らかにしている。さらにフーリエ展開係数の決定には、乱数発生サンプリング法によるほか、三角関数そのものを境界積分する全く独自の手法を考案している。後者の手法については、その適用範囲を拡充させるための研究が目下進行中である。
板垣 正文; C.A.Brebbia*
Boundary Elements, X, Vol.2, 12 Pages, 1988/00
偏微分方程式のコンピュータ向け解法として、近年、種々の工学分野で研究されている境界要素法が2次元のみならず3次元の中性子拡散問題に応用された。2次元及び3次元とも元の中性子拡散方程式は次元のひとつ少ない境界積分方程式に変換され、これを離散化して行列形式の境界要素式を得る。これにより、3次元問題であれば領域の境界表面における中性子束・中性子流のみを未知数として定義すればよい。それにも拘わらず、領域内部の中性子束分布を高精度で求めることができる。したがって差分法や有限要素法と比べて必要計算機容量が少なくて済み、また不規則幾何形状が容易にとりあつかえる等の利点がある。