Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Li, S.; Li, Y.; Lu, K.*; Lacroix, V.*; Dulieu, P.*
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 18 Pages, 2024/07
The stress intensity factor (SIF) solutions for subsurface flaws in flat plates are provided in Appendix A of ASME Boiler and Pressure Vessel Code Section XI. A part of the SIF solutions was initially provided in the 2015 edition. The solutions were obtained for the fourth order polynomial stress distribution base on the influence function method. The solutions were expanded in the 2021 edition for subsurface flaws near the surface of the plate. The additional solutions were obtained based on the J-integral from the elastic finite element analyses. However, recent investigations have found that there is a minor discrepancy in trend between the two sets of SIF solutions because they were obtained by using different numerical methods. Although the discrepancy is very small, the change in trend causes some difficulties in engineering applications. In this work, the SIF solutions are recalculated using the same numerical method based on the J-integral from elastic finite element analyses. The results are compared with the solutions in the current Section XI, RSE-M, and are finally cross-checked with the results obtained from an independent numerical model. The results are useful to eliminate the discrepancy in trend in the SIF solutions for subsurface flaws in flat plates in the current edition of Section XI.
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 5 Pages, 2024/07
内部欠陥が耐圧機器の表面近傍に検出された場合、この内部欠陥は接近性ルールに従って表面欠陥に置き換えなければならない。この内部欠陥から表面欠陥へのモデル化はASME(米国機械学会)規格のSection XIに採用されている。この接近性ルールの限界値は内部欠陥と自由表面の距離と欠陥深さによって決まる。この限界値は欠陥のアスペクト比に依存していない。本報告は、干渉効果の限界クライテリアを提案し、欠陥深さに依存し、かつ残余長さや欠陥のアスペクト比に依存する欠陥の接近性因子のための新しい限界値について述べる。
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of ASME 2023 Pressure Vessels and Piping Conference (PVP 2023) (Internet), 7 Pages, 2023/07
供用期間中の検査で原子力機器に欠陥が検出されたとき、ASME Code Section XIでは欠陥を評価するために許容欠陥寸法が用意されている。フェライト鋼では表IWB-3510-1に許容欠陥寸法があり、この許容欠陥寸法は応力拡大係数をもとに定められた。この論文の手法は塑性崩壊と脆性破壊の防止が含めるため、塑性崩壊については欠陥のアスペクト比に関かわらず一様な極限荷重の低下を考えている。脆性破壊の防止では表面欠陥の参照応力拡大係数を基にしている。この方法で種々なアスペクト比の許容寸法を規定している。さらに、この手法は機器の表面近傍にある内部欠陥と表面欠陥の整合性をとるために追加のパラメータを加えている。最後に、ASME規格の表IWB-3510-1の許容欠陥寸法の改定を提案する。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2023 Pressure Vessels and Piping Conference (PVP 2023) (Internet), 5 Pages, 2023/07
原子力機器に欠陥が検出された場合、ASME Code Section XIは許容欠陥寸法を用意している。フェライト鋼の許容寸法は表IWB-3510-1で与えられている。この寸法は、機器の肉厚、欠陥のアスペクト比と内部欠陥の機器表面への接近性の3つのパラメータに依存している。しかし、これらをグラフで表すといくつかの不具合があることが分かる。そこで、ロバストな手法でASME Codeの許容される表面欠陥の見直しの必要性に光を当てるものである。この論文は現行の不具合を詳細に述べ、改善案を提案するものである。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫; Mares, V.*
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 7 Pages, 2022/07
現行のASME Code Section XIでは、非平面状欠陥に対して簡易的な手法が提案されている。すなわち、非平面状欠陥面を最大主応力方向に投影し2つの平面状欠陥に分解する。しかしながら、この非平面状欠陥の簡易的な投影は荷重に対して、あるいは非平面状欠陥の傾きに対して常に保守的であると言えない場合がある。本論文は、ASME Codeのアプローチに保守性のある包括的な評価を実施し、現行のASME Code Section XIの不適正を克服した非平面状欠陥の代替アプローチを提案する。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2021 Pressure Vessels and Piping Conference (PVP 2021) (Internet), 5 Pages, 2021/07
欠陥が検出されたとき、この欠陥を有する耐圧機器の健全性はASME Section XI等の規格によって評価される。評価の最初のステップでは、検出された欠陥の形状を定める欠陥のモデル化を行うことである。ASME Section XIにおける欠陥モデル化手法では、非平面状欠陥は最大主応力方向に投影して、2つの平面状欠陥に分離して扱うように規定されている。このアプローチは欠陥評価を簡素化しているが、保守性が含まれている。本論文では、この欠陥モデル化手法の改善提案を行うために、現状の欠陥モデル化手法に基づく投影された平面状欠陥の応力拡大係数と実際の非平面状欠陥の混合モードの応力拡大係数について比較検討を行った。
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 7 Pages, 2020/08
検出された欠陥が近接している場合、維持規格で与えられる合体ルールにより、互いに干渉しあう欠陥は1つの欠陥に合体される。ASME Code Case N877-1は、複数の半径方向の平面状欠陥に対して代替合体ルールとして用意されたものである。欠陥の干渉の計算は、膜応力の下で実施されてきた。しかしながら、実際の機器に作用する付加荷重は一様な応力ではない。この論文の目的は、付加応力分布に曲げ応力が存在する場合のASME Code Case N877-1の妥当性を評価することにある。この目的のため、種々な応力分布と欠陥形状をカバーするようにした。欠陥の干渉に及ぼす効果は3次元のXEEM解析で評価した。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫; Mare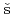 , V.*
, V.*
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 8 Pages, 2020/08
耐圧機器に複数欠陥が検出されたとき、欠陥の形状をはっきりと決めるために欠陥の特性化(形状の作成化)が行われる。この特性化は維持規格のルールに従ってなされる。最初のステップは、欠陥と機器の自由表面の干渉であり、2番目に欠陥と欠陥の干渉である。ASME Code Sec. XIでは如何にして欠陥の合体と自由表面の干渉の扱いが欠けており、欠陥の特性化が明確になっていない。いくつかの非現実な欠陥の配列ではあるが欠陥評価の代表例を図で論文の中に示す。この論文は、IWA-3300, IWB/IWC-3510-1の欠陥の特性化における合体欠陥の扱いを明確にするためにASME Codeの改定の技術根拠として用いられる。
Bouydo, A.*; Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫; Mare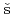 , V.*
, V.*
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 10 Pages, 2019/07
Flaw assessment according to Fitness-For-Service (FFS) codes is usually based on equations describing the impact of a single flaw in piping or pressure vessels components. However, when multiple flaws are detected, interaction rules are to be taken into account to evaluate whether these flaws should be combined into a larger flaw or should be evaluated as separate ones. In recent years, numerous works have be done to evaluate the conservatism of the interaction rules required by FFS code and, if needed, establish new characterization rules. These new characterization rules are based on the distance between flaws, their depths their lengths or a combination of these three parameters in order to reflect the level of interaction between adjacent flaws. A comparison, focusing on multiple surface planar flaws, between ASME B&PV Section XI current combination rules, other Fitness-For-Service codes and other interaction rules established by fellow authors in presented in this paper.
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of 2019 ASME Pressure Vessels and Piping Conference (PVP 2019) (Internet), 9 Pages, 2019/07
In the case of planar flaws detected in pressure components, flaw characterization plays a major role in the flaw acceptability assessment. When the detected flaws are in close proximity, proximity rules given in the Fitness-for-Service (FFS) Codes require to combine the interacting flaws into a single flaw. However, the specific combination criteria of planar flaws vary across the FFS Codes. These criteria are often based on flaw depth and distance between flaws only. However, the level of interaction depends on more parameters such as the relative position of flaws, the flaw sizes and their aspect ratio. In this context, revised and improved proximity criteria have been developed to more precisely reflect the actual interaction between planar flaws. Thanks to numerous three-dimensional XFEM analyses, a wide range of configurations has been covered, including interaction between two surface flaws, interaction between two subsurface flaws and interaction between a surface flaw and a subsurface flaw. This paper explains in detail the steps followed to derive such a generic proximity rules for radially oriented planar flaws.
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫; Li, Y.; Strnadel, B.*
Proceedings of 2018 ASME Pressure Vessels and Piping Conference (PVP 2018), 10 Pages, 2018/07
When multiple surface flaws are detected in pressure components, their potential interaction is to be assessed to determine whether they must be combined or evaluated independently of each other. This assessment is performed through the flaw characterization rules of Fitness-For-Service (FFS) Codes. However, the specific combination criteria of surface flaws are different among the FFS Codes. Most of the time, they consist of simple criteria based on distance between flaws and flaw depth. This paper aims at proposing alternative characterization rules reflecting the actual level of interaction between surface planar flaws. This interaction depends on several parameters such as the relative position of flaws, the flaw sizes and their aspect ratio. Thanks to numerous threedimensional XFEM simulations, best suited combination criteria for surface planar flaws are derived by considering the combined influence of these parameters.
Lacroix, V.*; Dulieu, P.*; Blasset, S.*; Tiete, R.*; Li, Y.; 長谷川 邦夫; Bamford, W.*; Udyawar, A.*
Proceedings of 2018 ASME Pressure Vessels and Piping Conference (PVP 2018), 10 Pages, 2018/07
When multiple flaws are detected in pressure retaining components during inspection, the first step of evaluation consists of determining whether the flaws shall be combined into a single flaw or evaluated separately. This combination process is carried out in compliance with proximity rules given in the Fitness-for-Service (FFS) Codes. However, the specific criteria for the rules on combining multiple flaws into a single flaw are different among the FFS Codes. In this context, revised and improved criteria have been developed, to more accurately characterize the interaction between multiple subsurface flaws in operating pressure vessels. This improved approach removes some of the conservatism in the existing ASME Code approach, which was developed in the 1970s based on two flaws interacting with each other. This paper explains in detail the methodology used to derive improved flaw proximity rules through three-dimensional FEM and XFEM analyses. After the presentation of the calculations results and the improved criteria, the paper also highlights the multiple conservatisms of the methodology using several sensitivity analyses.
長谷川 邦夫; Li, Y.; 勝又 源七郎*; Dulieu, P.*; Lacroix, V.*
Proceedings of 2017 ASME Pressure Vessels and Piping Conference (PVP 2017) (CD-ROM), 6 Pages, 2017/07
検出された内部欠陥が、機器の表面近傍にあるとき、応力拡大係数が大きくなる。このリガメントからの破壊を防ぐために維持規格では内部欠陥の接近性のルールがある。このルールによれば、内部欠陥を、内部欠陥のままにして破壊評価を扱うか、表面欠陥に置き換えて破壊評価を行う。表面欠陥に置き換えた場合、亀裂先端の応力拡大係数は増大する。この接近性のルールの考え方は世界各国の維持規格で同じであるが、具体的なクライテリアは異なる。そこで、世界各国の接近性クライテリアの紹介をするとともに、ASME規格で用いられるクライテリアをベースにして応力拡大係数を比較する。
長谷川 邦夫; Dulieu, P.*; Lacroix, V.*
Proceedings of 2017 ASME Pressure Vessels and Piping Conference (PVP 2017) (CD-ROM), 5 Pages, 2017/07
切欠底にある内部欠陥は、応力集中のため応力拡大係数の干渉効果が大きい。このため、内部欠陥は、切欠底から離れた位置で表面欠陥に置き換える必要がある。本論文は、応力集中場の応力拡大係数の干渉を示し、この干渉効果を基に切欠底に円欠陥があるときの接近性基準を提案するものである。