Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
徳田 伸二
Journal of Accelerator and Plasma Research, 5(1), p.87 - 108, 2000/00
トカマクにおける2次元Newcomb方程式に随伴する新しい固有値問題を導き、それを数値的に解いた。固有値問題の定式化では、重み関数と境界条件を固有値問題のスペクトルが実の可算個の固有値(点スペクトル)だけからなり、連続スペクトルをもたないように選んだ。本定式化はいくつかの著しい特徴をもつ。まず、この定式化により理想MHD的に安定な状態を特定できる。次に、抵抗性MHD安定性理論において本質的な役割をはたす外部領域接続データを、理想MHD的に臨界安定に近い場合にも計算することができる。
徳田 伸二; 渡辺 朋子*
プラズマ・核融合学会誌, 73(10), p.1141 - 1154, 1997/10
トカマクプラズマの抵抗性MHD安定性解析で重要な役割をはたす外部領域接続データを計算する新しい方法を提案する。この方法は、同時に、臨界安定状態を同定する理想MHD安定性解析の新しい方法でもある。この方法では、1次元の臨界安定な理想MHD状態を記述するNewcomb方程式に対する固有値問題を設定する。そして、Newcomb方程式の解の有限エネルギー部分をゼロに最も近い固有値をもつ固有関数と、その固有関数に垂直な成分に分ける。そして、垂直な成分の満たすべき特異方程式を導く。また、積分関数式を適用して有限エネルギー部分から接続データを計算する。接続データを解析的に求めることのできるm=1モード(m:ポロイダルモード数)に本方法を適用し、その有効性を実証した。
徳田 伸二; 渡邉 朋子*
JAERI-Research 97-034, 53 Pages, 1997/05
JAERI-Research-97-034.pdf:1.49MB
2枚の有理面に挟まれた外部領域におけるNewcomb方程式の大域解及び接続データの数値計算法を述べる。この接続データから各有理面のまわりの内部層方程式に対する境界条件が決定され、境界条件自身は2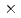
2行列(境界行列)で表される。大域解の変更(すなわち、解のうち無限エネルギー部分の変更)にともなう接続データの変換則を導き、境界行列の不変性を示した。また、テスト計算により、この数値計算法の妥当性を検証した。
徳田 伸二; 渡邉 朋子*
JAERI-Data/Code 95-011, 71 Pages, 1995/08
JAERI-Data-Code-95-011.pdf:1.94MB
1次元Newcomb方程式の外部領域接続データを数値的に求めるMARG1Dコードを開発した。接続データはトカマク・プラズマの抵抗性MHD安定性解析で重要な役割をはたす。MARG1Dコードでは接続データを境界値問題法および固有値問題法によって接続データを求める。解くべき問題に対応する変分原理を導き、有限要素法を適用する。臨界安定な場合を除けば、境界値問題法と固有値問題法は同等である。しかし、固有値問題法はいくつかの利点を持っている。すなわち、この方法は臨界安定な状態を同定できる理想MHD安定性解析の新しい方法である。また、臨界安定に近い場合の接続データを計算するにあたって数値的安定性を保証する。数値実験によってMARG1Dコードは高精度な接続データを与えることを示す。
