Spatial scale dependence of diffusion process in glass-forming liquids

ガラス形成液体における拡散過程の空間スケール依存性

古府 麻衣子   ; Faraone, A.*; Tyagi, M.*; 長尾 道弘*; 山室 修*

Kofu, Maiko; Faraone, A.*; Tyagi, M.*; Nagao, Michihiro*; Yamamuro, Osamu*

液体中の分子の自己拡散はFickの法則に従うと考えられている。van Hoveの自己時空相関関数は空間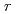に対しガウス型、時間に対し指数関数で記述される(デバイ緩和)。この場合、緩和時間は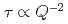の関係式を満たす。しかしながら、ガラス形成液体の自己拡散は非デバイ型のKWW (Kohlrausch-Williams-Watts)関数、、で記述されることが多い。では、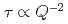の関係式は非デバイ型の拡散過程においても成り立つのだろうか?我々は、この問題に取り組むため、2種類の液体、分子液体(3メチルペンタン)とイオン液体(C4mimTFSI)の緩和時間の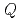依存性を詳細に調べた。測定には、NISTに設置された中性子スピンエコー分光器、後方散乱分光器、チョッパー分光器の3台の装置を用いた。両方の液体において、2つのQ位置でクロスオーバーが観測された。1つ目のクロスオーバーは構造緩和とのカップリング、2つ目のクロスオーバーはガウス-非ガウス転移と考えられる。今回の結果は2つのクロスオーバーに関する初めての実験的証拠である。

The self-diffusion of molecules in a liquid is basically governed by Fick's law. It is known that the self-part of the van Hove correlation function is written as the Gaussian function with respect to 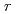and decays exponentially with time (Debye relaxation). In the case, the relaxation time obeys the relation 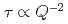. In glass-forming materials, however, the relaxation process is often described by the non-Debye KWW function, . A natural question arises as to whether the relation 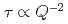is valid for the non- Debye diffusion process. To address this issue, we have investigated in detail the 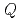-dependence of the relaxation times for two different types of liquid, a molecular liquid (3-methylpentane) and an ionic liquid (C4mimTFSI). The measurements were done using neutron spin echo, backscattering and chopper spectrometers at NIST. Two crossover points were clearly found. The first crossover can be due to coupling with structural relaxation and the second one is Gaussian to non-Gaussian transition. This is the first clear experimental evidence for the two crossover.