GPU-acceleration of locally mesh allocated two phase flow solver for nuclear reactors

原子炉に対する局所細分化二相流体解析手法のGPU高速化

小野寺 直幸   ; 井戸村 泰宏   ; Ali, Y.*; 山下 晋   ; 下川辺 隆史*; 青木 尊之*

Onodera, Naoyuki; Idomura, Yasuhiro; Ali, Y.*; Yamashita, Susumu; Shimokawabe, Takashi*; Aoki, Takayuki*

本研究では、ブロック型局所細分化(AMR)法に基づくPoisson解法のGPU高速化を実施した。ブロック型AMR法はGPUに適したデータ構造であり、複雑な構造物で構成された原子炉等の解析に必須な解析手法である。これに、最新の前処理手法であるマルチグリッド(MG)法を共役勾配(CG)法へと組み合わせることで、計算の高速化を実現した。MG-CG法を構成する計算カーネルをGPUスーパーコンピュータであるTSUBAME3.0上にて測定した結果、ベクトル-ベクトル和、行列-ベクトル積、およびドット積の帯域幅は、ピークパフォーマンスの約60%となり、良好なパフォーマンスを実現した。更に、MG法の前処理手法として、3段のVサイクル法および各段に対してRed-Black SOR法を適用した手法を用いて、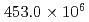格子点の大規模問題の解析を実施した結果、元の前処理付きCG法と比較して、反復回数を30%未満に削減すると共に、2.5倍の計算の高速化を達成した。

This paper presents a GPU-based Poisson solver on a block-based adaptive mesh refinement (block-AMR) framework. The block-AMR method is essential for GPU computation and efficient description of the nuclear reactor. In this paper, we successfully implement a conjugate gradient method with a state-of-the-art multi-grid preconditioner (MG-CG) on the block-AMR framework. GPU kernel performance was measured on the GPU-based supercomputer TSUBAME3.0. The bandwidth of a vector-vector sum, a matrix-vector product, and a dot product in the CG kernel gave good performance at about 60% of the peak performance. In the MG kernel, the smoothers in a three-stage V-cycle MG method are implemented using a mixed precision RB-SOR method, which also gave good performance. For a large-scale Poisson problem with 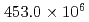cells, the developed MG-CG method reduced the number of iterations to less than 30% and achieved 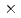2.5 speedup compared with the original preconditioned CG method.