Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
山本 敏久*; 北田 孝典*; 田川 明広; 丸山 学*; 竹田 敏一*
JNC TJ9400 2000-006, 272 Pages, 2000/02
多様な高速炉炉心の核特性に対する解析予測精度の向上を目的として、以下の3つの項目について検討を行った。第1部高速炉心の中性子スペクトルの誤差評価と計算精度向上策の検討高速実験炉「常陽」で用いられているスペクトルアンフォールディング法の精度を向上するため、初期推定スペクトル誤差を詳細に分析し、各々の誤差の大きさを定量的に評価するとともに、各誤差を積み上げることによって、より合理的な初期推定スペクトル誤差を評価することを試みた。検討の結果、初期推定スペクトル誤差に起因する誤差は相対的に小さく、断面積誤差に起因する誤差がほとんどであることがわかった。また、核分裂スペクトルの影響によって、数MeV以上の高速中性子束に無視できない量の誤差を生じることがわかった。第2部ガス冷却高速炉の解析手法に関する検討ガス冷却高速炉では、通常のNa冷却炉に比べて、冷却材チャンネルが体積割合に占める比率が大きく、顕著な中性子ストリーミング効果が現れることが予想される。一方、Na冷却炉用に提唱されている既存の手法では、冷却材チャンネルと平行な方向の拡散係数が無限大となり、そのまま適用することができない。本研究では、Kohlerが提唱した軸方向バックリングを考慮した方向依存拡散係数の概念を拡張し、ガス冷却炉でも正確に中性子ストリーミング効果が評価できる手法の検討を行った。第3部水冷却高速炉の解析手法に関する検討低減速の水冷却炉に対して、解析手法の違いによりどの程度計算結果に影響が現れるかについて検討を行った。軽水炉においては、燃料ペレット中の重核種の自己遮蔽効果が強い空間依存性を持つことが知られており、燃料ペレットを複数の領域に分割して評価する手法が用いられている。水冷却高速炉においても、冷却材として水を使用する以上、同様の問題が現れる可能性がある。検討の結果、燃料ペレット中の重核種の自己遮蔽効果の空間依存性は小さく、燃料領域を1領域として扱っても、臨界性、転換比ともに解析精度には問題が出ないことが確認された。
柴本 泰照; 久木田 豊*; 中村 秀夫; Park, H. S.*; 安濃田 良成
Proceedings of 8th International Conference on Nuclear Engineering (ICONE-8) (CD-ROM), p.12 - 0, 2000/00
溶融金属と冷却材の相互作用(MFCI)時には、冷却材の蒸気が大量に発生するが、蒸気生成速度によって蒸気爆発になる場合と爆発に至らない場合がある。後者は穏やかなMFCI事象と呼ばれ、本研究ではその現象解明研究の一環として、高温の溶融金属中にジェット状に注水する体系についての基礎研究を行っている。これまで、このような研究例は限られており、特に、多くの溶融物は可視光には不透明なため、その中の水の挙動を可視化することは困難であった。そこで本研究では、高速度撮影中性子ラジオグラフィ(NRG)を利用することで、可視化に対する問題を解決するとともに、発生蒸気量や水ジェット貫入深さ等について定量計測を試みた。実験では、あらかじめ試験容器内に高温の溶融金属を満たしたところに室温の水ジェットを注入した。その結果、より高温のメルトに注入させた方が、蒸気発生量がより少ない結果となった。これは、高温の場合、水/溶融金属の界面上に安定な蒸気膜が形成され、これが伝熱の阻害に寄与し、蒸気発生が少なかったためと考えることができる。
Peter, J. Collins
PNC TN9410 97-034, 35 Pages, 1997/04
大洗工学センターの基盤技術開発部炉心技術開発室に滞在している間、私は高速増殖実証炉(DFBR)のために炉定数ライブラリを行うプロジェクトに参加した。このライブラリは、核断面積(微分データ)を高速炉に関する実験(積分データ)と結びつけ、DFBRの設計に充分な精度を確保しようとするものである。私は、USDOEとPNCの協定の基づきZPPR装置において実施された大型高速炉心臨界実験JUPITERの企画とそのデータ利用に関して豊富な経験を有している。大洗での私の役割は主に、過去にロスアラモス国立研究所(LANL)で実施された非常に硬いスペクトルでの高速炉臨界実験を実験データベースに加えることであった。これらの実験炉心に関するデータは本報告書に記載されている。我々はANL-Westで、動燃のABLEコードと同じ機能を持つGMADJコードを使って行った研究により、現在のDFBRが対象としている伝統的なMOX炉心だけではなく、このプロジェクトではより多くの実験を用いる必要があることを明らかにした。動燃ではこの点への認識がこれまで為されていなかったので、本報告書で議論している。LANLで行われた高速スペクトルの臨界実験データは、私が収集した誤差評価に関する情報とともにまとめた。これらの実験の最大の目的は臨界性データを得ることであったので、炉定数調整で必要となる誤差の相関(共分散)情報は報告されていないが、実験誤差の最大の要因は燃料組成誤差であることが分かっている。このLANL実験は、米国でENDF/Bライブラリの各バージョンを開発する際には、その積分テストに重要な役割を果たしてきた。DFBRのための炉定数開発に対しては、これらのLANLデータは、通常の軟らかいスペクトルを持つLMFBRでは得られないMeV領域の情報を提供できる。
市原 潔*
JAERI-Data/Code 97-011, 25 Pages, 1997/03
複素数連立一次方程式およびエルミート固有値問題を数値計算によって解いた場合の誤差の分析に必要なデータ取得を支援するサブルーチンを開発した。複素数連立一次方程式については、残差ベクトルのノルム、係数行列の条件数、解の誤差限界を計算する。エルミート行列固有値問題については、Korn-Katoの公式に基づいて、固有値の存在範囲を計算する。上記それぞれについて、逐次計算機用と並列計算機用が用意されている。本報告書は、サブルーチンで使用している精度評価公式の要点と、サブルーチンの利用方法についてまとめたものである。
文沢 元雄; 菱田 誠
Laser Anemometry 1995 (FED-Vol. 229), 0, p.51 - 56, 1995/00
高温ガス炉スタンドパイプ破断事故時空気浸入挙動解明の一環として、浮力駆動置換流の流量測定を行った。平均値の評価は、流動状況が不規則な上昇及び下降流を呈するので、速度バイアスを考慮して行った。誤差評価は、非正規分布の統計量を調べるのに用いる中心極限定理とStudentのt分布を使用して行った。その結果、置換流の流速分布及び流量を測定でき、レーザー流速計を用いた計測システムとデータ処理プログラムを開発することができた。置換流の配管内分布は、上下容器の温度差が増加すると一山分布から二山分布へ変化することがわかった。また下部容器球面温度が底面温度より低い場合には両者が同じ温度の場合よりも置換流量が低下することが明らかとなった。
島崎 潤也
計測自動制御学会論文集, 19(2), p.179 - 181, 1983/00
状態遷移行列の計算には、指数関数のパデ近似を用いる方法がすでに提案されているが、正確な誤差評価のもとで使用されていない。そのため小さなサンプリング時間でシステム行列の固有値の大きさに注意してパデ近似を利用しなければならない。そこで、大きなサンプリング時間でもまた広い範囲の固有値の場合でもパデ近似を有効に利用する方法の開発が必要である。本論文では指数関数のパデ近似式に対して誤差式を導き、それを用いて指数関数を指定の精度で計算する方法を提出した。この方法は縮小した変数の指数の指数関数にパデ近似を用い、ついで拡大するものである。得られた結果は変数を行列にした場合に適用でき、状態遷移行列を設定した精度で効率よく計算するのに有効である。
島崎 潤也
計測自動制御学会論文集, 19(2), p.182 - 184, 1983/00
常微分方程式の初期値問題に対する数値斛法にはEuler法、Runge Kutta法に始まり種々の方法が利用できる。しかしこれらの方法は数値斛法斛としては有用であるが、制御問題等の離散時間モデルとしては利用できない。そこで制御問題等で使用できるいわゆる離散型状態方程式を導くことを目的として、1つの積分近似公式を導いた。求めた積分近似公式は近似次数により異なり、次数を上げることにより近似精度が向上すること、公式中の係数が指数関数の同次パデ近似と同じことを示した。また公式の応用例として、定係数線形状態方程式に対する離散時間モデル作成の方法を与え、さらに時間変数系と非線形系に対する処理方法を述べた。
山内 通則*; 関 泰; 飯田 浩正
JAERI-M 8739, 36 Pages, 1980/03
1次摂動理論に基づく感度解析法を用いて、核融合実験炉JXFRの構造材の断面積に対する主要な核特性値の感度を解析した。同種の報告がすでに以前なされているが、その後の検討で使用した感度計算コードSWANLAKEに変換の際に生じたプログラムエラーのあることが判明したのでそれを修正し、主要な内容について再計算を行なった。対象とした特性値は、超電導トロイダルコイル外側部分の(n、p)反応率、内側部分の桐原子はじき出し率およびリチウム領域のトリチウム生成反応率である。再計算の結果は前回得られた評価の大要を打ち消すものではないが、計算値に多少の違いが生じたので値を修正するとともに、それに基づく評価の内容も更新した。感度計算値の修正の結果、断面積の不確かさに起因する(n、p)反応率と桐原子はじき出し率の誤差は、それぞれ約50~70%、25~65%となった。これは前回計算された値より約100%大きく、それだけ断面積精度に対する要求が増大したといえる。
佐藤 貞夫; 宮本 喜晟
JAERI-M 7059, 57 Pages, 1977/04
DREAM-FLOWコードは、ピン・イン・ブロック型燃料を用いた高温ガス炉炉心の流れの遷移域における摩擦係数のばらつきに注目した多並列流路モデルによる流量の誤差評価を目的に開発したものである。本コードは、計算手段としてモンテカルロ法を適用し、流れが遷移状態である場合の摩擦係数に対して乱数を発生させ、この統計的性質を仮定した上で流量の誤差評価を行っている。本コードの使用によって摩擦係数のばらつきによる冷却材流量とそれに伴う燃料最高温度の統計的性質が明らかにできる。本報告書はこのコードの計算モデルと計算方法ならびに使用方法について解説したものである。DREAM-FLOWコードはFACOM230-75用FORTRAN-IVで書かれており、所要記憶容量は125K語である。
三谷 浩
Journal of Nuclear Science and Technology, 13(8), p.413 - 422, 1976/08
被引用回数:0原子炉の計算において、高次摂動項を求める一般的方法が著者によって展開されたが、高次摂動級数はすべての問題に対して収斂するとは限らない。この問題を数学的に厳密に取り扱うことは非常に困難であるが、ヒルベルト空間の線形作用素に対して展開されたKatoの定理を用いると、一群拡散近似の範囲内で厳密な取り扱いが可能になる。得られた結果は極めて簡潔であり、原子炉系での基本的な量のみを含んでいる。即ち、条件1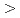 {2-d|
{2-d|
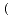
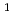
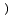 |+3|
|+3|
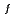
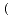
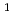
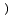 |}が満たされる時、摂動級数は収束し、吸収断面積のみが変化する時には、高次摂動法の誤差は
|}が満たされる時、摂動級数は収束し、吸収断面積のみが変化する時には、高次摂動法の誤差は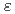
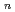
 (2-d)
(2-d)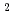 |
|
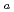
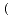
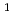
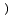 |
|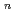
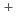
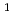 /(1-2|
/(1-2|
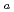
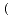
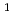
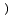 |/d)で与えられる。ここでdは非摂動系の固有値のレベル間隔、
|/d)で与えられる。ここでdは非摂動系の固有値のレベル間隔、
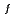
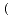
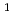
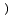 ,
,
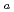
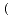
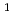
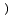 は核分裂及び吸収断面積が変化した時の一次反応度であり、
は核分裂及び吸収断面積が変化した時の一次反応度であり、
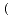
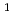
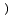 =
=
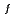
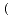
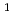
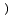 +
+
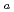
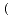
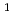
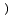 である。原型炉及び1000MWe高速炉に対する数値計算の結果、前者ではほとんどすべての摂動実験に対して級数は収束し、後者については|
である。原型炉及び1000MWe高速炉に対する数値計算の結果、前者ではほとんどすべての摂動実験に対して級数は収束し、後者については|
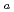
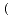
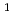
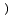 |
|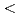 0.12,|
0.12,|
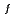
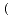
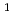
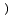 |0.09?K/Kで摂動級数が収束することが明らかになった。
|0.09?K/Kで摂動級数が収束することが明らかになった。
植木 太郎
no journal, ,
統計数理的手法の開発において、当該手法の限界性能評価は、信頼性確保のために重要である。そこで、世界の実効増倍率問題として知られるモンテカルロ法臨界計算に関して、その特質を極度に抽出した例題を作成し、既存手法による実効増倍率タリーの統計誤差評価とバイアス補正の妥当性評価を実施した。