Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
丸山 修平
Proceedings of International Conference on Physics of Reactors 2022 (PHYSOR 2022) (Internet), 10 Pages, 2022/05
本論文は新しい均質化法「Boundary Condition Free Homogenization (BCFH)」を提案した。従来の均質化法では、セル計算において特定の境界条件または周辺領域を仮定することにより、炉心計算とセル(集合体)計算を分離している。これらの仮定にはあいまいさや近似があり、評価結果の精度の低下を引き起こす原因にもなる。BCFHはこれらの問題を回避し、均質化等に係るセル計算の精度を向上させることを目的としている。著者は反応率保存に関連するセル内の物理量が流入部分中性子流に対して保存されるという条件を課した。すなわち、セル平均中性子束と流出部分中性子束の応答行列は均質-非均質系で同じになるものとした。これにより得られる断面積,SPH因子,不連続因子等の均質化パラメーターは特定の境界条件に依存しなくなる。このようにして得られた新しい均質化パラメータは、従来のベクトル形式から行列形式に拡張されたものとなる。BCFHの性能を調査するために、我が国のナトリウム冷却高速炉の炉心概念を使用して数値実験を行った。その結果、BCFHは従来の方法と比較して制御棒の反応度価値や反応率分布を評価するのに特に有効であることがわかった。この結果に基づき、BCFHは炉心解析における1つの有望な均質化の概念になりえると結論付けた。
Wang, Z.; Duan, G.*; 松永 拓也*; 杉山 智之
International Journal of Heat and Mass Transfer, 157, p.119919_1 - 119919_20, 2020/08
被引用回数:26 パーセンタイル:78.69(Thermodynamics)Enforcing accurate and consistent boundary conditions is a difficult issue for particle methods, due to the lack of information outside boundaries. Recently, consistent Neumann boundary condition enforcement is developed for the least squares moving particle semi-implicit method (LSMPS). However, the Robin boundary cannot be straightforwardly considered by that method because no computational variables are defined on the wall boundary. In this paper, a consistent Robin boundary enforcement for heat transfer problem is proposed. Based on the Taylor series expansion, the Robin boundary condition for temperature is converted to the fitting function of internal rather than boundary particles and incorporated into least squares approach for discretization schemes. Arbitrary geometries can be easily treated due to the use of polygons for wall boundary. A convergence study was firstly carried out to verify the consistency. Then, numerical tests of 1-D and 2-D heat conduction problems subjected to mixed boundary conditions were performed for verification, and good agreements with theoretical solutions were observed. Natural convection problems with different boundary conditions in an annulus were carried out for further validations of heat-fluid coupling. Excellent agreements between the present and literature results were demonstrated.
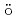 dinger equation
dinger equation内海 隆行*; 矢部 孝*; Koga, J. K.; 青木 尊之*; 関根 優年*
Computer Physics Communications, 157(2), p.121 - 138, 2004/02
被引用回数:13 パーセンタイル:50.69(Computer Science, Interdisciplinary Applications)光量子科学の一環として開発されている高強度・短パルス・短波長レーザーを原子へ照射する際のイオン化現象を利用して、高調波発生,X線レーザー発振,高Z多価イオン源といった応用が期待されている。強レーザー電場中のイオン化ではイオン化安定化などの非線形現象が支配的となるが、この解析には通常の摂動論的手法の適用には限界があり非摂動論的手法の開発が重要となる。近年では、非摂動論的手法として時間依存シュレディンガー方程式を直接解く手法が最も有効な手段であると認識されはじめている。本論文では、流体方程式などの双曲型偏微分方程式の数値解析手法として開発された3次補間擬似粒子法(CIP)を基底関数の観点から再構成することにより、時間依存及び非時間依存シュレディンガー方程式の高精度数値解法としてCIP-BS法を提案する。CIP-BS法は、偏微分方程式及び境界条件を一意的に帯状対角行列のみを用いた離散方程式に変換し、計算効率を向上させることができる。本手法の有効性を調和振動子,平面波,クーロン場,morseポテンシャル場における解析により示す。また、この手法がさまざまな物理現象を記述する偏微分方程式の汎用的数値解法としての拡張性を有することを述べる。
藤村 統一郎*; 奥村 啓介
JAERI-Research 2002-024, 27 Pages, 2002/11
低減速スペクトル炉等の6角形状の炉心を解析する拡散コードの原型版を開発し、その反復解法を高速化するため、さまざまな収束加速法の適用性について検討した。本3次元コードMOSRA-Prismは、6角形状の炉心を正3角柱に分割し、その中の中性子束分布を3次の多項式で近似する多項式展開ノード法に基づいている。多群拡散コードとしての反復解法は、通常の内側反復法と外側反復法を採用するが、内側反復に適応的加速法、外側反復に中性子源外挿法を適用し、その有効性を確認した。本報告書では、コードの数値解法の元となる多項式展開ノード法の定式化の概要を説明するとともに、さまざまなサンプル計算で得られた、収束加速法の局所的な効率及び全体的な効率について検討する。また、コード開発過程で新たに導出した真空境界条件の一般的な記述法についても述べる。
徳田 伸二; 渡辺 朋子*
統計数理研究所共同研究リポート, 110, p.70 - 77, 1998/03
トカマクプラズマ配位における2次元Newcomb方程式に随伴する固有値問題を提案する。この定式化においては重み関数(運動エネルギー積分)と有理面における境界条件を適切に選び、固有値問題のスペクトルが実可算の固有値(点スペクトル)だけから成り、連続スペクトルを持たないようにした。この定式化によって理想磁気流体力学的運動に対して、不安定状態だけでなく安定状態の特定が可能となった。
功刀 資彰; 江里 幸一郎*; 清水 昭比古*
Proc. of 2nd Japan-Central Europe Joint Workshop on Modelling of Materials and Combustion, 0, p.205 - 208, 1996/00
核融合炉のプラズマディスラプション時には、プラズマ崩壊によって、瞬時に莫大なエネルギーがプラズマ対向壁(PFC)へ投下され、PFCは溶融・蒸発する。この損耗量の評価が機器寿命を決定する重要な因子の一つであることから、各種高エネルギービームを用いた模擬実験や解析が行われている。しかし、これら実験値と解析値は一致せず、その原因解明が急がれている。本研究では、この食い違いの原因とされている溶融蒸発過程の原子挙動(クラスター生成)や解析コードの境界条件(熱平衡性)の妥当性を検討することを目的とし、高エネルギー加熱源としてレーザー、ターゲット材としてPFC候補材のモリブデンを対象とした光モンテカルロ-分子動力学シミュレーションを実施した。その結果、緩やかな定常的な加熱時にはターゲット材料は単調な溶融蒸発挙動を示し、蒸発原子同士によるクラスター生成も見られるが、原子運動の統計量の検討から溶融蒸発界面での熱平衡性は達成されていることが示された。また、急速なパルス的強加熱時には衝撃波的な圧力波が材料中を音速で伝播し、熱平衡は達成されず、特に、材料表面では沸騰のようなボイドが発生することなどが示された。
藤村 統一郎
Computer Physics Communications, 82, p.111 - 119, 1994/00
被引用回数:1 パーセンタイル:21.46(Computer Science, Interdisciplinary Applications)三次元中性子輸送問題を高精度で解くための定式化を行い、検証計算を実施した。二重有限要素法に基づいた変分法による定式化では、空間変数に一次関数を適用するとともに、角度変数に階段関数を適用している。ここに、多角柱形状の原子炉体系を反射条件を用いて解く場合、新しく開発した体系打切り誤差解消アルゴリズムにより、厳密な離散式が導出される。この解法の検証のため、二つの問題について計算を行った。MOZART炉心をモデル化した問題では、不規則な要素分割に対する非等方散乱計算においても、この解法が有効に働くことが示された。また、NEA-CRPのLWRをモデル化したベンチマーク問題では、粗いメッシュでも固有値や中性子束が、他の輸送方程式の解法による解と同精度に求まることが示された。
高野 誠
JAERI-M 91-108, 25 Pages, 1991/07
二次元Sn計算コードTWOTRANは炉心解析等に以前から広く使われているコードである。TWOTRANコードで扱える形状の一つにR-Z形状があるが、外周の境界条件としては無限配列セル計算の場合、白色境界条件又は反射境界条件しか用意されていない。本報では、実際の使用済PWR燃料棒セル計算をTWOTRANコードのR-Z形状で解析した際に生じた問題点を示し、一次元SnコードANISNやモンテカルロコードKENOによる結果との比較検討により、R-Z形状の外周境界条件としては白色境界条件および反射境界条件が不適当となる場合があることを示した。このため、新たに「白色反射境界条件」を提案し、これをTWOTRANコードに組み込み、他の境界条件を使用した場合と比較した結果、最も良好な結果を示すことが判明した。
C-J.Jeong*; 奥村 啓介; 石黒 幸雄; 田中 健一*
Journal of Nuclear Science and Technology, 27(6), p.515 - 523, 1990/06
MOX燃料棒の稠密格子から成る高転換軽水炉体系におけるセル計算手法の精度を共鳴計算手法(NR,IR近似、超詳細群衝突確率法)及びセル形状(六角、円筒)と境界条件(完全反射、等方反射)に関して検討、確認を行った。一連の計算は、高転換軽水炉に関する国際ベンチマークで採用された格子モデルを参照体系として行った。中性子増倍率、転換比、減速材ボイド特性等の諸物理量を広範囲な減速材対燃料体積比、燃料種類と富化度に対して評価し、連続エネルギーモンテカルロ法による計算値との比較により、これらの計算手法の予測精度と適用性を明確にした。IR近似の精度はNR近似に比べて良好であるが、特にスペクトルが硬くなる場合に悪くなる。また、円筒化近似の精度は、ウラン燃料格子系に比べ、プルトニウム燃料系で悪化することが確認された。
岩崎 淳一; 市川 博喜; 鶴田 晴通
JAERI-M 84-159, 147 Pages, 1984/09
JRR-3改造計画の一環として、20%濃縮U・Alx燃料を用いた炉心の核設計を行った。本報告書は、その結果に使用した、炉心および反射体内各領域での臨界計算用少数群断面積、炉心軸方向バックリングおよび制御棒境界条件について説明している。
藤村 統一郎; 松村 正弘*; 中原 康明
JAERI-M 83-144, 40 Pages, 1983/09
本稿は、三次元幾何形状における定常、多群中性子輸送問題に対する二重有限要素法に基づくガレルキン法のアルゴリズムとその特徴について述べたものである。定式化においては、現実の原子炉の形状をできる限り正確に模擬するため、空間要素として三角柱要素と四角柱要素の組合せを採用すると共に、中性子束の角度分布を滑らかに表現するため、角度空間において重なりをもつ六つの基底を採用している。本解法の特徴は境界条件を陽に記述すること、および平面の層に沿って次々と節点を走査する反復法にあり、その収束加速法の新しい提案もなされる。この解法に基づく計算コードが開発され、その概要についての解説も示される。また、今迄に実施した実在規模の問題を含む計算の経験に基づき、差分法のコードとの比較をもとに二重有限要素解の特徴が示される。
藤村 統一郎; 中原 康明; 松村 正弘*
Journal of Nuclear Science and Technology, 20(7), p.620 - 623, 1983/00
被引用回数:4 パーセンタイル:54.18(Nuclear Science & Technology)本稿は、3次元幾何形状における定常、多群中性子輸送問題に対し、ガレルキン型の解放に基づく新しい、簡単な定式化が提案される。定式化は、空中間要素と角度要素を用いる二重有限要素法によっている。現実の核燃料施設の形状をできる限り正確に模擬するため、三角柱要素と四角柱要素の組合せを採用するとともに、中性子束を滑らかにするため、角度空間においては相関をもつ6つの角度要素を試験的な基底として採用している。本解法の特徴は境界条件を陽に記述すること、および中性子源外插法において核分裂項を厳密に記述することにある。これらの方法の遂行性は、実在規模の問題を含む数個の見本計算例で示される。