Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
相羽 信行; 徳田 伸二; 石澤 朋子*
Journal of Plasma Physics, 72(6), p.1127 - 1131, 2006/12
被引用回数：1 パーセンタイル：3.50(Physics, Fluids & Plasmas)トカマク核融合装置において高性能プラズマを長時間保持することを実現するうえで、外部電磁流体(MHD)不安定性の発生を抑えることは重要な課題であり、特にこの不安定性のアスペクト比に対する依存性は装置設計を行ううえで考慮すべき要因の一つである。本研究ではこれまで開発を続けてきたMHD安定性解析コードMARG2Dの特徴である「広いトロイダルモード数nの範囲にわたって解析ができる」という特長を生かすことで、nが1から10までの外部MHDモードの安定性に対するアスペクト比の依存性を調べた。その結果、外部MHDモードから決まるプラズマ圧力の限界はアスペクト比を小さくすることで高くなることを確認した。またプラズマを囲む完全導体壁の位置がプラズマ表面に近い場合、アスペクト比が小さくなるにつれて圧力限界を決める外部モードのトロイダルモード数は大きくなることを示した。さらにこの原因が、アスペクト比を小さくしたことによって異なるポロイダルモード間のトロイダル結合が強くなり、その結果nの小さいモードを強く安定化する導体壁の影響が強く表れるためであることを、MARG2Dコードで得られる固有関数を比較することによって明らかにした。
松本 太郎; 内藤 裕志*; 徳田 伸二; 岸本 泰明*
Nuclear Fusion, 45(11), p.1264 - 1270, 2005/11
被引用回数：15 パーセンタイル：45.00(Physics, Fluids & Plasmas)核融合プラズマの中心部のような高温になると電気抵抗が小さくなるとともに、電子慣性等の非衝突効果(運動論的効果)が磁気再結合過程に深くかかわる。本研究では、これらプラズマの粒子性を物理的に忠実に取り扱う観点から、ジャイロ運動論的粒子モデルを用いた3次元シミュレーションにより、反転磁気シア配位トカマクにおける磁気再結合を伴うMHD不安定性に対する運動論的効果の解明を目的とした。反転磁気シア配位において二つの共鳴面の距離が近いと、互いの共鳴面における摂動が結合し、ダブルテアリングモード(DTM)と呼ばれる内部モードが生じる。高温プラズマにおいて電子慣性により誘起される運動論的DTMは、抵抗性モデルにより予期されるものより、速い内部崩壊を引き起こし得ることが明らかとなった。さらに、内部崩壊により掃き出された電流は、DTMが作り出した静電ポテンシャルに導かれて凹型に再集中し得ることが明らかになった。本研究は、低ベータ負磁気シア実験におけるディスラプション機構の一端を示しており、またDTMを経た電流分布の再分配により負磁気シア配位を再構築し得ることを示唆している。
相羽 信行*; 徳田 伸二; 石澤 朋子*; 岡本 正雄*
Plasma Physics and Controlled Fusion, 46(11), p.1699 - 1721, 2004/11
被引用回数：3 パーセンタイル：9.92(Physics, Fluids & Plasmas)ニューコム方程式の理論をトカマクにおける低-n外部モードに適用し、安定性行列を計算する方法を確立した。安定性行列によって外部モードによるプラズマポテンシャルエネルギーの変化を摂動のプラズマ表面での値で表すことができる。この方法を用いて、理想外部モードのスペクトルの性質を詳細に調べた。それには外部モードと内部モードの結合,通常シア配位と逆シア配位の安定性の違いなどが含まれる。これらの結果は抵抗性壁モードの安定性解析にも有益である。
徳田 伸二; 相羽 信行*
Journal of Plasma and Fusion Research SERIES, Vol.6, p.207 - 209, 2004/00
ニューコム方程式の研究の最新の進展について報告する。主として、高nキンクモードであるピーリングモードも含んだ外部モードの解析について述べる。また、低nモードについては、抵抗性壁モードの解析にも有用な理論を展開した。
Mukhovatov, V.*; 嶋田 道也; Chudnovskiy, A. N.*; Costley, A. E.*; Gribov, Y.*; Federici, G.*; Kardaun, O. J. F.*; Kukushkin, A. S.*; Polevoi, A. R.*; Pustovitov, V. D.*; et al.
Plasma Physics and Controlled Fusion, 45(12), p.235 - 252, 2003/12
被引用回数：59 パーセンタイル：84.17(Physics, Fluids & Plasmas)ITERはDT燃焼によって約0.5GWの核融合エネルギーを発生する最初の磁場閉じ込め装置である。最近の2, 3年の間に得られた研究成果によって、ITERのHモード運転においてQ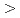
10を達成できることがほぼ確実となった。それらには、三角形度を高くすることによって得られたグリーンワルド密度付近における良好なHモード閉じ込め,理論モデルに基づく炉心プラズマ閉じ込めの予測の改良,D/Tイオンとヘリウム中性粒子との弾性衝突を考慮したダイバータモデル計算によるヘリウム灰除去効率の改善,NTM(新古典テアリング・モード)のフィードバック制御による
値の改善,ELM物理の理解の進展とELM緩和法の開発,ディスラプション緩和法の検証などがある。ITERはその機動性を用いて定常及び中間領域(ハイブリッド)運転を行うことも可能である。この論文においては、おもに誘導運転のプラズマ性能、及び定常運転のために要請される性能について議論を行う。
JT-60チーム
JAERI-Review 2003-029, 197 Pages, 2003/11
JAERI-Review-2003-029.pdf:13.06MB
本報告書は、2001年及び2002年にJT-60Uにおいて行った実験の結果をまとめたものである。完全非誘導電流駆動状態での高核融合三重積(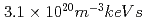
)の達成,高規格化ベータ値(
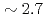)の長時間(7.4秒間)維持,高核融合エネルギー増倍率(
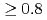以上)の時間の伸長(0.55秒間),高密度(グリーンワルド密度の
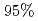)における閉じ込め改善(ITER98(y,2)スケーリングの0.9倍)の実現,電子サイクロトロン波電流駆動を用いた新古典テアリングモードの実時間制御,中心ソレノイドコイルを用いない革新的運転シナリオの開発等、炉心プラズマの高性能化,高性能炉心プラズマの定常化に対する進展について述べる。また、電流駆動,輸送障壁,MHD不安定性,高エネルギーイオン,ディスラプション,不純物,ダイバータプラズマ,プラズマ壁相互作用等に関する物理課題の研究,計測装置,加熱装置の開発についても報告する。
栗田 源一; 津田 孝; 安積 正史; 石田 真一; 竹治 智*; 逆井 章; 松川 誠; 小関 隆久; 菊池 満
Nuclear Fusion, 43(9), p.949 - 954, 2003/09
被引用回数：31 パーセンタイル：66.72(Physics, Fluids & Plasmas)原型炉の開発における二つの重要な課題は高ベータ化と低放射化材料の開発である。後者の低放射化材料の開発に関しては、現在低放射化フェライト鋼が最有力候補であると考えられているが、強磁性体であるためMHD不安定性による摂動磁場を吸い込むことによってMHD安定性を劣化させ前者のベータ限界を下げる可能性がある。ここでは、フェライト鋼(強磁性体)壁の効果を含んだMHD安定性解析を行うことによって限界ベータに対する強磁性体壁の影響を調べた。
Konovalov, S. V.; Mikhailovskii, A. B.*; Tsypin, V. S.*; Galv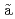
o, R. M. 0.*; Nascimento, I. C.*
Plasma Physics Reports, 29(9), p.779 - 784, 2003/09
被引用回数：2 パーセンタイル：6.02(Physics, Fluids & Plasmas)内部抵抗性壁モード(RWM)のドリフト効果による安定化の問題を理論的に調べた。このモデルでは、ドリフト効果が無いとき、壁が無ければ不安定で理想壁があるときは安定であることを基本的に仮定している。抵抗性壁モードの発生初期はテアリングモードの不安定化で始まるとして、テアリングモードの指標を壁がある場合と無い場合について求め、反磁性ドリフトの効果が重要であることを理論的に示した。内部抵抗性壁モードの安定性を、現存する多くのトカマク装置に対して検討し、現状のトカマク装置ではドリフトによる安定化効果はほとんどないが、トカマク炉クラスにおいては、安定化効果があることを明らかにした。
徳田 伸二
Proceedings of 30th EPS Conference on Controlled Fusion and Plasma Physics (CD-ROM), 4 Pages, 2003/00
二次元Newcomb方程式に随伴する固有値問題を解くことにより、理想MHD的な摂動に対するトカマクプラズマの安定性を判定することができる。この固有値問題は、不安定なプラズマに対する成長率を与えない。しかし、成長率と固有値の間の関係を与える分散関係式を構築でき、それによって、成長率を決定することができる。分散関係式は理想MHD的な摂動に対して臨界安定に近いMHDモードの安定性を解析するための効果的な、かつ、高速な方法を提供し、かつ、臨界安定に近い場合の非理想MHDモードに対し拡張できると期待される。
竹治 智; 諫山 明彦; 小関 隆久; 徳田 伸二; 石井 康友; 及川 聡洋; 石田 真一; 鎌田 裕; 閨谷 譲; 芳野 隆治; et al.
Fusion Science and Technology (JT-60 Special Issue), 42(2-3), p.278 - 297, 2002/09
被引用回数：7 パーセンタイル：3.03(Nuclear Science & Technology)トカマクプラズマの高圧力定常運転の実現への寄与を念頭に、高ポロイダルベータモード,負磁気シアモード等JT-60Uにおける閉じ込め改善トカマク放電における磁気流体力学的(MHD)安定性の研究成果を総括した。閉じ込め改善プラズマを特徴付ける周辺部及び内部輸送障壁は、それらが形成する大きな圧力勾配とそれに伴うブートストラップ電流により、局所的あるいは広域的MHD安定性に重要な影響を及ぼす。まず、閉じ込め改善放電の広域的安定性限界は、低n(トロイダルモード数)キンクモードで規定され、プラズマ圧力分布の尖鋭度の低減,プラズマ形状の高三角度化及び導体壁の近接により安定性限界を改善できる。局所的安定性では、周辺部輸送障壁にかかわる周辺部局在モード(ELM),内部輸送障壁にかかわる内部輸送障壁局在モード(BLM),抵抗性交換型モードについてその発生機構等を明らかにした。さらに、高圧力プラズマの長時間維持において問題となる、新古典テアリングモード(NTM),抵抗性導体壁モード(RWM)のMHD特性とその安定化について議論した。
Smolyakov, A. I.; Lazzaro, E.*; Coelho, R.*; 小関 隆久
Physics of Plasmas, 9(1), p.371 - 374, 2002/01
被引用回数：8 パーセンタイル：27.16(Physics, Fluids & Plasmas)新古典テアリングモードは、ブートストラップ電流を用いた高プラズマの性能向上を制限するものとして精力的な研究が行われている。イオン慣流電流(イオン分極電流)は磁気島の安定化効果があると考えられており、本論文はシアープラズマ流のイオン慣性電流への影響を調べた。その結果、磁気島端において局所プラズマ流があり、それによる磁気島内に循環する流れがある場合に、磁気島の安定化効果があることを示した。一方、磁気島内に流れのない場合は不安定化に働く。
徳田 伸二
Theory of Fusion Plasmas, p.87 - 102, 2002/00
トカマクのMHD安定性解析で重要な役割を果すNewcomb方程式と境界層方程式の解法の最近の発展について述べる。特に、2次元Newcomb方程式を自由境界モードに適用し、自由境界モードの安定性行列を求める方法について詳しく述べる。
小関 隆久; 諫山 明彦
プラズマ・核融合学会誌, 77(5), p.409 - 419, 2001/05
トロイダル・プラズマにおいて磁気島内でのブートストラップ電流の減少による新古典テアリングモード(NTM)の発生について、修正ラザフォード方程式に基づいて解説している。ここでは、NTMの基礎理論、実験観測について述べ、NTM発生の値スケーリングと成長機構について議論している。また、NTMのエネルギー閉じ込めへの影響及び電子サイクロトロン電流駆動(ECCD)による安定化について紹介している。
徳田 伸二
プラズマ・核融合学会誌, 77(3), p.276 - 283, 2001/03
トロイダルプラズマ閉じ込めシステムの抵抗性磁気流体力学安定性に関する漸近接続理論で現れる内部層方程式を数値的に解く新しい解法スキームも提案する。このスキームは内部層方程式を初期値問題として解く。時間に関して完全陰差分近似を適用して、径方向に関する微分だけを含む方程式を導く。このようにして導かれた微分方程式の解は、無限遠点における、与えられた漸近条件を満たさなければならない。この接続問題は、有限差分法の適用できる境界値問題に変換される。本スキームにより、プラズマの全領域で運動方程式を解くことなく、磁気島の発展等、内部層のダイナミックスのシミュレーションが可能となる。
徳田 伸二
Journal of Accelerator and Plasma Research, 5(1), p.87 - 108, 2000/00
トカマクにおける2次元Newcomb方程式に随伴する新しい固有値問題を導き、それを数値的に解いた。固有値問題の定式化では、重み関数と境界条件を固有値問題のスペクトルが実の可算個の固有値(点スペクトル)だけからなり、連続スペクトルをもたないように選んだ。本定式化はいくつかの著しい特徴をもつ。まず、この定式化により理想MHD的に安定な状態を特定できる。次に、抵抗性MHD安定性理論において本質的な役割をはたす外部領域接続データを、理想MHD的に臨界安定に近い場合にも計算することができる。
徳田 伸二; 渡辺 朋子*
Physics of Plasmas, 6(8), p.3012 - 3026, 1999/08
被引用回数：56 パーセンタイル：83.06(Physics, Fluids & Plasmas)トカマクのような軸対称トロイダルプラズマにおける2次元ニューコム方程式の新しい固有値問題を提示する。この定式化においては、固有値問題のスペクトルが可算無限個の実数の固有値(点スペクトル)のみからなり、連続スペクトルを持たないように、重み関数(運動エネルギー積分)と有理面における境界条件とを設定した。理想m=1モードへ適用し、本定式化が不安定状態のみならず、安定状態も特定できること、及び、数値的に得られた固有関数が有理面で理論的に予想される特異性を示すことを実証した。
ディスラプション・プラズマ制御・MHDグループ
Nuclear Fusion, 39(12), p.2251 - 2389, 1999/00
ITERの設計建設のために必要なトカマクプラズマのMHD安定性、ディスラプション特性、運転限界についての物理基準を示した。日、米、露、欧の4極の専門家グループを中心に世界中のITER物理R&Dの成果をレビューした。MHD安定性では、理想MHD、壁による安定化効果、抵抗性壁モード、鋸歯状振動、新古典ティアリングモード、エラー磁場不安定性、ELM等についての特性を示した。ディスラプションでは、熱消滅、プラズマ電流消滅、垂直位置移動現象(VDE)、ハロー電流、逃走電子、ディスラプション頻度の各特性をレビューし、ITERの設計基準に反映した。運転限界では、密度限界、値限界等についてレビューし、炉心プラズマとして安定な性能が得られる領域を示した。
小関 隆久
プラズマ・核融合学会誌, 74(9), p.998 - 1005, 1998/09
トカマク・プラズマにおいて形成された内部輸送障壁によって励起されるMHD不安定性について、最近の研究成果を報告している。内部輸送障壁は、主に高ポロイダルプラズマと負磁気シアプラズマにおいて得られ、これに伴ってMHD不安定性が発生している。高ポロイダルプラズマにおける、低nキンク・バルーニングモードによるコラップスの発生、新古典テアリングモードの可能性、BLM現象について述べている。また、負磁気シアプラズマにおける、凹状電流分布による限界、抵抗性交換型モード等について言及している。最後に、今後の研究の課題及び展望について述べている。
p mode plasmas in the Japan Atomic Energy Research Institute Tokamak-60 upgrade竹治 智; 鎌田 裕; 小関 隆久; 石田 真一; 滝塚 知典; 閨谷 譲; 徳田 伸二
Physics of Plasmas, 4(12), p.4283 - 4291, 1997/12
被引用回数：16 パーセンタイル：49.96(Physics, Fluids & Plasmas)高ポロイダルベータ(p)モードは、内部輸送障壁に起因する閉じ込め改善モードである。内部輸送障壁は、その内側の閉込め特性を著しく改善する一方で、その近傍で強い圧力勾配を形成するために、局所的な不安定性の原因となることが分かってきた。このことは、プラズマ内部の局所的な圧力・電流分布がプラズマ安定性に極めて重要であることを示している。本論文では、内部輸送障壁近傍に局在する不安定性(BLM)の実験解析・数値解析を行い、その発生機構の解明を試みた。実験解析の結果は、BLMが局在した理想低トロイダル数(n)キンクモードであることを示唆した。MHD安定性数値解析の結果、内部輸送障壁による局所的な圧力勾配とそれに伴うブートストラップ電流の効果により、内部輸送障壁近傍に局在する理想低nキンクモードが存在し得ることを発見した。これらにより、BLMを同定しその発生機構を解明した。
徳田 伸二; 渡邉 朋子*
JAERI-Data/Code 97-040, 105 Pages, 1997/10
JAERI-Data-Code-97-040.pdf:2.32MB
トカマクのような2次元軸対象トロイダルプラズマの磁気流体力学的(MHD)安定性解析において重要な役割を果たす2次元Newcomb方程式の新しい解法を考案し、それに基づくコード(MARG2D)を開発した。新しい解法では2次元Newcomb方程式を固有値問題として解く。この際、固有関数が有利面における小さい解と正則解を正しく捉えるように重み関数(運動エネルギー積分)と有理面における境界条件を選定し、従来の困難を克服した。このコードを使うことにより、2次元配位における理想MHDモードの臨界安定状態の同定が可能になる。また、このコードは抵抗性MHD安定性解析において外部領域接続データを計算する上で不可欠である。従来の理想MHDコードERATOJとのベンチマークテストにより、MARG2Dコードで安定状態及び臨界安定状態が同定できることを実証した。
