Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
仁平 猛*; 岩田 忠夫
JAERI-M 92-099, 28 Pages, 1992/07
複合Simpson公式を積分の上下限が可変であるn次元積分に拡張した。この拡張はn次級数の漸化式によって示した。この方法により、n次元の積分に対し、Newton-Cotes式による計算構造を明らかにした。その結果、Newton-cotes式に対応する求積式が容易に組み立てられるようになった。若干の計算例を示し、2次元および3次元積分に対する誤差の評価を誤差項を用いて記述した。
M.L.Mehta*
J.Math.Phys., 17(12), p.2198 - 2202, 1976/12
被引用回数:16例えば2つの共鳴レベルの相関を求めようとする場合、共有確立密度 Q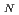
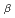 (x1,x2,・・・・・・xn)=Const.
(x1,x2,・・・・・・xn)=Const.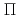 |xj-xk|
|xj-xk|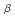 1
1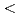 j
j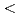 k
k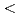 N を使って表すことができる。この際2変数を除く他の変数についての積分が必要であるが、その計算法が複雑なため、より高次の相関を求めることがあきらめられているのが現状である。この論文では著者およびDysonによって見出された有力な計算法を使うことによってこの種の高次相関を求め得ることを示した。
N を使って表すことができる。この際2変数を除く他の変数についての積分が必要であるが、その計算法が複雑なため、より高次の相関を求めることがあきらめられているのが現状である。この論文では著者およびDysonによって見出された有力な計算法を使うことによってこの種の高次相関を求め得ることを示した。