Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
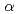 -clustering in atomic nuclei from first principles with statistical learning and the Hoyle state character
-clustering in atomic nuclei from first principles with statistical learning and the Hoyle state character大塚 孝治; 阿部 喬*; 吉田 亨*; 角田 佑介*; 清水 則孝*; 板垣 直之*; 宇都野 穣; Vary, J. P.*; Maris, P.*; 上野 秀樹*
Nature Communications (Internet), 13, p.2234_1 - 2234_10, 2022/04
被引用回数:47 パーセンタイル:96.78(Multidisciplinary Sciences)多くの原子核では核子の独立粒子模型がよい近似であり、それが原子核構造の出発点となっているが、一部の軽い原子核では陽子2個と中性子2個からなるアルファ粒子が局在しているアルファクラスターを構成要素としてもよいと考えられている。しかしながら、アルファクラスターそのものを観測することは困難であり、それがどの程度よい近似なのかは軽い核を理解する上で重要である。本研究では、核力から出発した第一原理モンテカルロ殻模型計算により、ベリリウム同位体および炭素12の多体波動関数を得た。物体固定系での密度分布の計算結果から、ベリリウム同位体では2個のアルファクラスターが局在していることを示した。また、炭素12では基底状態は比較的液滴模型に近く、ホイル状態として知られる第一励起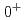 状態はアルファクラスターと液滴状態が混合したクロスオーバーとしてとらえられることがわかった。これらの解析に、デンドログラムという統計的学習手法が有効であることもわかった。
状態はアルファクラスターと液滴状態が混合したクロスオーバーとしてとらえられることがわかった。これらの解析に、デンドログラムという統計的学習手法が有効であることもわかった。
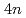 self-conjugate nuclei in
self-conjugate nuclei in 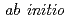 no-core Monte Carlo shell model calculations with nonlocal
no-core Monte Carlo shell model calculations with nonlocal 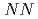 interactions
interactions阿部 喬*; Maris, P.*; 大塚 孝治*; 清水 則孝*; 宇都野 穣; Vary, J. P.*
Physical Review C, 104(5), p.054315_1 - 054315_22, 2021/11
被引用回数:11 パーセンタイル:77.46(Physics, Nuclear)近年、大規模数値計算の進化に伴い、核力のみを出発点として原子核の性質を得ることを目的とした第一原理核構造計算が盛んに行われているが、未だに酸素16を超える核子多体問題を近似なしに解くのは困難である。本論文では、広い配位空間を採用した無芯殻模型によって第一原理計算を行う手法として、モンテカルロ殻模型による近似解をもとに、配位空間の大きさを無限大に外挿する手法を提案し、その有効性を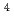 He,
He, 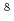 Be,
Be, 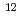 C,
C, 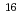 O,
O, 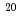 Neの5核種について調べた。特に、Daejeon16相互作用という短距離相関の弱い核力を使えば、
Neの5核種について調べた。特に、Daejeon16相互作用という短距離相関の弱い核力を使えば、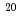 Neでも、外挿にともなう束縛エネルギーの不定性をかなり小さくすることが可能となった。
Neでも、外挿にともなう束縛エネルギーの不定性をかなり小さくすることが可能となった。
清水 則孝*; 阿部 喬*; 本間 道雄*; 大塚 孝治*; 富樫 智章*; 角田 佑介*; 宇都野 穣; 吉田 亨*
Physica Scripta, 92(6), p.063001_1 - 063001_19, 2017/06
被引用回数:33 パーセンタイル:82.08(Physics, Multidisciplinary)モンテカルロ殻模型の手法およびその応用について概説する。モンテカルロ殻模型は、効率的に多体基底を生成することによって、従来の直接対角化では計算不可能だった物理系に対する殻模型計算を目指した手法である。このレビュー論文では、モンテカルロ殻模型のここ10年以内の発展をまとめた。手法面では、エネルギー分散を用いた外挿による厳密解の推定法や共役勾配法の導入による効率的な基底生成など、数値計算面では、より効率的な並列化や計算機の実効性能を高める数値計算アルゴリズムなどについて概説する。最近の応用としては、非常に大きな模型空間が必要な第一原理計算および中性子過剰なニッケル領域とジルコニウム領域の計算結果を紹介する。後者の中性子過剰核領域では、変形共存に興味が集まっているが、モンテカルロ殻模型では、変形の分布を解析するT-plotと呼ぶ新しい手法を開発することによって、これらの原子核の変形を直感的に理解することが可能となった。この手法は、軽い原子核のクラスター状態を調べるのにも有用である。
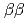 decay of
decay of 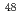 Ca
Ca岩田 順敬*; 清水 則孝*; 大塚 孝治*; 宇都野 穣; Men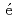 ndez, J.*; 本間 道雄*; 阿部 喬*
ndez, J.*; 本間 道雄*; 阿部 喬*
Physical Review Letters, 116(11), p.112502_1 - 112502_6, 2016/03
被引用回数:83 パーセンタイル:93.76(Physics, Multidisciplinary)ニュートリノレス二重ベータ崩壊は、ニュートリノがマヨラナ粒子であることを示す決定的な証拠となるが、未だその観測に成功していない。その核行列要素を理論的に正確に与えられれば、実験に大きな制約を与えることになるが、核構造模型による不定性が大きいというのが現状である。この研究では、最も正確な核行列要素を与えると期待される大規模殻模型計算によって、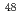 Caのニュートリノレス二重ベータ崩壊の核行列要素を調べた。
Caのニュートリノレス二重ベータ崩壊の核行列要素を調べた。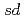 殻から
殻から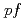 殻へ励起する配位を取り入れた大規模計算によって、従来の
殻へ励起する配位を取り入れた大規模計算によって、従来の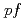 殻計算に比べ、約30
殻計算に比べ、約30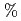 の核行列要素の増大を得た。核構造の観点からは、この増大は、対相関と核行列要素が密接に関係していることによってもたらされたものである。
の核行列要素の増大を得た。核構造の観点からは、この増大は、対相関と核行列要素が密接に関係していることによってもたらされたものである。
宇都野 穣; 大塚 孝治*; 清水 則孝*; 角田 佑介*; 本間 道雄*; 阿部 喬*; 水崎 高浩*; 富樫 智章*; Brown, B. A.*
Proceedings of International Conference on Nuclear Theory in the Supercomputing Era 2014 (NTSE 2014), p.29 - 34, 2016/00
スーパーコンピュータを用いた大規模数値計算による原子核理論研究の進展を議論する本国際会議において、大規模殻模型計算の発展に関する招待講演を行う。現在、非常に軽い核では生の核力に基づく第一原理計算が行われているが、質量数20程度以上の核に対して第一原理計算を行うのは当面の間困難である。そこで、質量数100程度までの中重核構造は、殻模型が有力な手法である。殻模型計算を行うには、有効相互作用が必要となるが、未だにそれを正確に得ることは難しく、特に殻構造に関わる部分に大きな不定性が残されている。本講演では、発表者らによって提唱された統一的に殻構造を記述する有効相互作用によって、様々な領域の不安定核構造が非常によく理解されるようになったことを示す。その例として、軽い核から中重核までの魔法数領域、カルシウム、ニッケル、スズ同位体を採り上げ、中心力とテンソル力による殻構造変化およびそれに伴う変形共存現象などについてのいくつかの話題を紹介する。
富樫 智章*; 清水 則孝*; 宇都野 穣; 阿部 喬*; 大塚 孝治*
Procedia Computer Science, 29, p.1711 - 1721, 2014/06
被引用回数:1 パーセンタイル:28.71(Computer Science, Theory & Methods)核構造計算では、非直交なスレーター行列式間のハミルトン行列要素を数値計算する必要がしばしばあり、多くの場合、それは最も計算時間を要する部分となる。本論文では、GPGPU(GPUによる汎目的計算)を利用してこの数値計算を効率よく行うことが可能となったことを報告する。発表者らの以前の論文で、非直交なスレーター行列式間のハミルトン行列要素の計算は、行列積に帰着させることが可能であることが示された。この手法は浮動小数点計算の回数に対するメモリアクセスの比を大きくすることが可能なため、メインメモリへのアクセスがボトルネックとなるGPGPU計算にも有効である。モンテカルロ殻模型計算コードにGPGPU計算を実装し、計算速度を測定したところ、理論性能1.31TFLOPSのGPUに対し、最大0.6TFLOPSを超える実効性能を得ることができた。模型空間が大きいほど実効性能が高くなるため、大規模計算に対して特に有効である。
宇都野 穣; 大塚 孝治*; 清水 則孝*; 本間 道雄*; 水崎 高浩*; 角田 佑介*; 阿部 喬*
EPJ Web of Conferences, 66, p.02106_1 - 02106_8, 2014/03
被引用回数:15 パーセンタイル:96.56(Physics, Nuclear)原子核構造を研究するための有力な手法の一つである殻模型における最近の発展と、それを用いた中性子過剰核などのエキゾチック核構造の理解の進展についてレビューする。殻模型における二つの重要な要素である有効相互作用と大規模核構造計算手法に関する発表者らの研究成果をまとめる。有効相互作用については、殻構造変化を引き起こすモノポール相互作用の統一的理解が喫緊の課題であるが、発表者らは数年前にテンソル力を取り入れた普遍的モノポール相互作用を提唱した。それを中性子数28領域のエキゾチック核及びアンチモン同位体の殻模型計算に取り入れ、核構造計算を行った結果、幅広い質量領域で有用であることが示された。大規模量子多体計算については、直接対角化法の限界を超えうる手法である、モンテカルロ殻模型計算を採り上げる。その進展により中重核の核構造を正確に計算できるようになったことを示し、その例として、中性子過剰ニッケル同位体における変形共存の結果を紹介する。
宇都野 穣; 清水 則孝*; 大塚 孝治*; 阿部 喬*
Computer Physics Communications, 184(1), p.102 - 108, 2013/01
被引用回数:13 パーセンタイル:59.70(Computer Science, Interdisciplinary Applications)原子核物理では、生成座標法など、非直交スレーター行列式間のハミルトニアン行列要素の計算がしばしば必要とされる。本論文では、最新のスカラー型プロセッサにおいてこの行列要素を最も効率的に計算する計算手法を与えた。非直交スレーター行列式間のハミルトニアン行列要素はハミルトニアン行列要素と密度行列がかかわる4重ループの計算に帰着されることが知られている。ハミルトニアン行列要素に多くゼロを含むため、4重ループをそのまま計算すると非常に効率が悪いが、対称性を考慮することで密行列とベクトルの積に帰着されることを示した。さらに、多くの行列要素を同時に求める場合、密行列の積として表されることを導いた。密行列の積に式変形することで、スカラー型計算機の理論性能に近い計算効率が得られることを示し、従来使われていた計算手法の5倍から10倍の計算効率を得た。
阿部 喬*; Maris, P.*; 大塚 孝治*; 清水 則孝*; 宇都野 穣; Vary, J. P.*
Physical Review C, 86(5), p.054301_1 - 054301_18, 2012/11
被引用回数:70 パーセンタイル:94.14(Physics, Nuclear)核子間の相互作用として正の相互作用を用いた核構造計算は第一原理計算と呼ばれるが、その中でも一粒子状態を非常に数多くの調和振動子波動関数で展開した殻模型的手法は有力な手法として知られている。本論文では、殻模型的手法のうち、完全配位相互作用計算(FCI),モンテカルロ殻模型計算(MCSM),無芯殻模型計算(NCSM)の3手法を多体計算手法の観点から比較した。FCIは、与えられた一粒子空間内すべての多体状態を取り入れるもので、計算が可能ならば最も正確な値を出す方法である。しかし、4主殻取り入れた場合、炭素12など核子数が多い系のFCI計算は現段階では不可能である。NCSMは、多体状態の調和振動子量子数で制限をかける計算であり、多くの一粒子状態数を取り入れることはできるが、多粒子多空孔状態の記述に難がある。一方、MCSMは、FCI計算可能な系ではFCIとほとんど同じエネルギー値を与え、それが不可能な系においても計算可能なことが示され、今後非常に有力となる手法であることがわかった。
清水 則孝*; 阿部 喬*; 角田 佑介*; 宇都野 穣; 吉田 亨*; 水崎 高浩*; 本間 道雄*; 大塚 孝治*
Progress of Theoretical and Experimental Physics (Internet), 2012(1), p.01A205_1 - 01A205_27, 2012/00
被引用回数:133 パーセンタイル:96.05(Physics, Multidisciplinary)モンテカルロ殻模型は、1990年代後半に提案され数多くの成果を挙げてきたが、近年、新しい方法論及び計算手法を導入し、「京」のようなスーパーコンピュータに適した手法となるとともに、従来のモンテカルロ殻模型では到達できなかった、より計算が困難な物理系へも適用可能となった。方法論に関しては、エネルギー分散を利用した外挿法を導入することによって、エネルギー固有値を非常に精度よく計算することが可能となった。また、数値計算アルゴリズムをより効率的なものに置き換え、並列計算手法を改良したことによって、高い計算効率を得られるようになった。その結果、第一原理的殻模型計算や中性子過剰ニッケル領域など、従来の手法では困難だった計算も可能となり、それらの計算結果の例も示した。
清水 則孝*; 宇都野 穣; 水崎 高浩*; 大塚 孝治*; 阿部 喬*; 本間 道雄*
Physical Review C, 82(6), p.061305_1 - 061305_4, 2010/12
被引用回数:46 パーセンタイル:90.09(Physics, Nuclear)殻模型は核構造を正確に記述することのできる優れた模型であるが、重い核では対角化すべき行列が大きすぎて計算できないという実用上の限界があった。モンテカルロ殻模型法は、こうした困難な問題に対しても良い近似を与える方法であるが、変分原理に基づいているため、エネルギー固有値は厳密解よりも高くなるとともに、厳密解からどれくらい離れているかわからないという問題点があった。本論文では、ハミルトニアンの期待値とその分散に非常に強い相関があることに基づき、モンテカルロ殻模型の結果から厳密解を外挿法によって求める新しい方法を導入した。また、外挿に必要なハミルトニアンの2乗の行列要素を効率的に計算する新しい公式を導いた。原子力機構及び東京大学の大型計算機を用い、厳密解がわかっている系に新しい外挿法を適用してその有用性を確かめ、さらにハミルトニアン行列が大きすぎてこれまで厳密解が計算できなかった系に対しても精度の良いエネルギーを与えることに成功した。
宇都野 穣; 清水 則孝*; 阿部 喬*; 大塚 孝治*
no journal, ,
モンテカルロ殻模型や生成座標法など、複数のスレーター行列式を重ね合わせることで多体系の波動関数を表現する手法では、ハミルトニアンなど二体演算子の行列要素に最も多くの計算時間が費やされる。したがって、その高速化が数値計算上重要な課題である。われわれは、新しいアルゴリズムにより、その数値計算を著しく高速化することに成功した。一つめの改良点は、従来リストベクトルを用いて表現されてきた疎な二体行列要素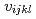 を、対称性を利用することで密なブロック行列に書き換えることにより、浮動小数点演算の回数を半減させた。また、これによって、高速な数値計算ライブラリである、レベル2のBLASが使える形になっている。さらに二つめの改良点として、重ね合わせるべき波動関数をまとめることによって、レベル2のBLASよりも高速なレベル3のBLASが使えるよう書き直した。最近の計算機上でテストした結果、これらの改良により、従来のアルゴリズムよりも5倍以上の高速化を実現した。
を、対称性を利用することで密なブロック行列に書き換えることにより、浮動小数点演算の回数を半減させた。また、これによって、高速な数値計算ライブラリである、レベル2のBLASが使える形になっている。さらに二つめの改良点として、重ね合わせるべき波動関数をまとめることによって、レベル2のBLASよりも高速なレベル3のBLASが使えるよう書き直した。最近の計算機上でテストした結果、これらの改良により、従来のアルゴリズムよりも5倍以上の高速化を実現した。