Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
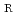 for negative stress ratios R based on trend in experimental data for fatigue crack growth rates of austenitic stainless steels for ASME code Section XI
for negative stress ratios R based on trend in experimental data for fatigue crack growth rates of austenitic stainless steels for ASME code Section XINegyesi, M.*; 山口 義仁; 長谷川 邦夫; Lacroix, V.*; Morley, A.*
Journal of Pressure Vessel Technology, 147(2), p.021201_1 - 021201_7, 2025/04
被引用回数:0 パーセンタイル:0.00(Engineering, Mechanical)Fatigue crack growth rates for stainless steels in air environment are provided by the ASME Code Section XI. When the stress ratio R is positive from 0 to 1, the scaling parameter SR increases with the increasing ratio R, and the crack growth rates increase with the increasing stress ratio R. When R is less than 0, the parameter SR=1. Hence, fatigue crack growth rates under negative R ratios are independent of stress ratios R according to the ASME Code Section XI. However, from the literature survey, experimental data reveal that the fatigue crack growth rates decreases with decreasing R ratios below zero. The objective of this paper is to assess fatigue crack growth rates under such negative stress ratios for stainless steels in air environment. An equation determined from trends in experimental data surveyed in this study is proposed for negative stress R ratios to calculate the parameter SR for the ASME Code Section XI.
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 5 Pages, 2024/07
内部欠陥が耐圧機器の表面近傍に検出された場合、この内部欠陥は接近性ルールに従って表面欠陥に置き換えなければならない。この内部欠陥から表面欠陥へのモデル化はASME(米国機械学会)規格のSection XIに採用されている。この接近性ルールの限界値は内部欠陥と自由表面の距離と欠陥深さによって決まる。この限界値は欠陥のアスペクト比に依存していない。本報告は、干渉効果の限界クライテリアを提案し、欠陥深さに依存し、かつ残余長さや欠陥のアスペクト比に依存する欠陥の接近性因子のための新しい限界値について述べる。
Negyesi, M.*; 山口 義仁; 長谷川 邦夫; Lacroix, V.*; Morley, A.*
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 8 Pages, 2024/07
Fatigue crack growth rates da/dN for stainless steels in air environment are provided by the ASME Code Section XI. The fatigue crack growth rates are given by da/dN = C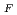 (
(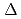 K)
K)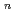 , where C
, where C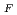 is the fatigue crack growth rate coefficient, n is the fatigue crack growth rate exponent and
is the fatigue crack growth rate coefficient, n is the fatigue crack growth rate exponent and 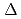 K is the stress intensity factor range. The coefficient C
K is the stress intensity factor range. The coefficient C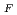 contains a temperature parameter S
contains a temperature parameter S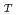 , and a scaling parameter, S
, and a scaling parameter, S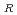 , which is a function of the stress ratio R. When the stress ratio R is positive from 0 to 1, the parameter S
, which is a function of the stress ratio R. When the stress ratio R is positive from 0 to 1, the parameter S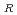 increases with increasing the ratio R, and da/dN increases with increasing stress ratio R. When R is less than 0, the parameter is given by S
increases with increasing the ratio R, and da/dN increases with increasing stress ratio R. When R is less than 0, the parameter is given by S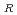 = 1.0. Accordingly, fatigue crack growth rates under negative stress ratio are always constant, independent of stress ratios. This means that a cyclic stress state with a minimum that is compressive is considered to cause the same degree of crack growth as one with the same range but a zero minimum. However, from the results of literature survey, experimental data reveal that the fatigue crack growth rates decrease with decreasing R ratios below zero, i.e. negative stress ratios. The objective of this paper is to assess fatigue crack growth rates under such negative stress ratios for stainless steels in air environment. An equation determined from trends in experimental data is proposed for negative R ratios for calculating the parameter S
= 1.0. Accordingly, fatigue crack growth rates under negative stress ratio are always constant, independent of stress ratios. This means that a cyclic stress state with a minimum that is compressive is considered to cause the same degree of crack growth as one with the same range but a zero minimum. However, from the results of literature survey, experimental data reveal that the fatigue crack growth rates decrease with decreasing R ratios below zero, i.e. negative stress ratios. The objective of this paper is to assess fatigue crack growth rates under such negative stress ratios for stainless steels in air environment. An equation determined from trends in experimental data is proposed for negative R ratios for calculating the parameter S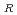 for the ASME Code Section XI, Appendix Y, based on the literature surveyed in this study.
for the ASME Code Section XI, Appendix Y, based on the literature surveyed in this study.
Negyesi, M.*; 河 侑成; 長谷川 邦夫; Lacroix, V.*
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 6 Pages, 2024/07
Allowable stresses for pipes are determined by combining failure stresses and safety factors. When predicting the plastic collapse failure stresses for high toughness ductile pipes, flow stresses of the pipe materials are indispensable. The flow stress is usually given by the average of the yield strength and the ultimate tensile strength. Inservice Inspection of the American Society of Mechanical Engineers (ASME) Code Section XI states to use the yield strengths and the ultimate tensile strengths defined by the ASME Code Section II Materials. The ASME Code Section XI also states that actual measured yield strengths and ultimate tensile strengths are possible to be used, alternatively. Values of yield strength and ultimate tensile strength given by the ASME Code Section II are conservative, corresponding to lower bound values. Then, it is easily inferred that the allowable stresses calculated by the code given flow stress are lower than the allowable stresses calculated by the actual measured flow stress. The objective of this paper is to compare the plastic collapse failure and allowable stresses based on both the code and actual flow stresses for pipes with circumferential flaws subjected to bending and tensile loading. In addition, it is demonstrated that allowable flaw sizes based on both flow stresses do not differ much at low allowable stress. However, when the allowable stress is large, the allowable flaw size based on the code flow stress is substantially lower compared to that based on the actual flow stress.
Li, S.; Li, Y.; Lu, K.*; Lacroix, V.*; Dulieu, P.*
Proceedings of ASME 2024 Pressure Vessels & Piping Conference (PVP 2024) (Internet), 18 Pages, 2024/07
The stress intensity factor (SIF) solutions for subsurface flaws in flat plates are provided in Appendix A of ASME Boiler and Pressure Vessel Code Section XI. A part of the SIF solutions was initially provided in the 2015 edition. The solutions were obtained for the fourth order polynomial stress distribution base on the influence function method. The solutions were expanded in the 2021 edition for subsurface flaws near the surface of the plate. The additional solutions were obtained based on the J-integral from the elastic finite element analyses. However, recent investigations have found that there is a minor discrepancy in trend between the two sets of SIF solutions because they were obtained by using different numerical methods. Although the discrepancy is very small, the change in trend causes some difficulties in engineering applications. In this work, the SIF solutions are recalculated using the same numerical method based on the J-integral from elastic finite element analyses. The results are compared with the solutions in the current Section XI, RSE-M, and are finally cross-checked with the results obtained from an independent numerical model. The results are useful to eliminate the discrepancy in trend in the SIF solutions for subsurface flaws in flat plates in the current edition of Section XI.
長谷川 邦夫; Li, Y.; Udyawar, A.*; Lacroix, V.*
International Journal of Pressure Vessels and Piping, 204, p.104952_1 - 104952_7, 2023/08
被引用回数:2 パーセンタイル:20.09(Engineering, Multidisciplinary)高靭性の耐圧配管に軸方向の亀裂が検出された場合、極限荷重基準によって破壊応力が推定される。亀裂配管の許容応力は破壊応力と安全率の組み合わせで導かれる。すなわち、亀裂深さと長さが許容応力から決定される。この許容応力と貫通亀裂の破壊応力の比較から、許容亀裂は一様でない。この許容亀裂は3つの特性に分かれる。1つは、破断前漏洩(LBB)と亀裂の安定成長、2つめはLBBは成り立たないが亀裂の安定成長。3つめはLBBが成り立たず亀裂の不安定成長である。検査技術者やユーザーは、LBBが成り立たず亀裂の不安定成長の特性を有する3つめの許容亀裂に対し特別な注意を払う必要がある。この特別な注意を要求される許容亀裂深さと長さの境界を表す近似式を記述する。
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of ASME 2023 Pressure Vessels and Piping Conference (PVP 2023) (Internet), 7 Pages, 2023/07
供用期間中の検査で原子力機器に欠陥が検出されたとき、ASME Code Section XIでは欠陥を評価するために許容欠陥寸法が用意されている。フェライト鋼では表IWB-3510-1に許容欠陥寸法があり、この許容欠陥寸法は応力拡大係数をもとに定められた。この論文の手法は塑性崩壊と脆性破壊の防止が含めるため、塑性崩壊については欠陥のアスペクト比に関かわらず一様な極限荷重の低下を考えている。脆性破壊の防止では表面欠陥の参照応力拡大係数を基にしている。この方法で種々なアスペクト比の許容寸法を規定している。さらに、この手法は機器の表面近傍にある内部欠陥と表面欠陥の整合性をとるために追加のパラメータを加えている。最後に、ASME規格の表IWB-3510-1の許容欠陥寸法の改定を提案する。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2023 Pressure Vessels and Piping Conference (PVP 2023) (Internet), 5 Pages, 2023/07
原子力機器に欠陥が検出された場合、ASME Code Section XIは許容欠陥寸法を用意している。フェライト鋼の許容寸法は表IWB-3510-1で与えられている。この寸法は、機器の肉厚、欠陥のアスペクト比と内部欠陥の機器表面への接近性の3つのパラメータに依存している。しかし、これらをグラフで表すといくつかの不具合があることが分かる。そこで、ロバストな手法でASME Codeの許容される表面欠陥の見直しの必要性に光を当てるものである。この論文は現行の不具合を詳細に述べ、改善案を提案するものである。
Journeau, C.*; Delacroix, J.*; Gu var, C.*; Testud, V.*; Brackx, E.*; Porcheron, E.*; Bouland, A.*; Berlemont, R.*; 池田 篤史
var, C.*; Testud, V.*; Brackx, E.*; Porcheron, E.*; Bouland, A.*; Berlemont, R.*; 池田 篤史
Science Talks (Internet), 6, p.100215_1 - 100215_9, 2023/05
One of the important challenges for the decommissioning of the damaged reactors of the Fukushima Daiichi Nuclear Power Station (1F) is the fuel debris retrieval. The URASOL (URAnium and aeroSOL) project has been undertaken by the French consortium laboratories consisting of ONET, CEA, and IRSN for JAEA. It aims at acquiring basic data on the generation and characteristics of radioactive aerosols from the thermal or mechanical processing of fuel debris simulant. Prototypic fuel debris samples were fabricated based on the average of the lower head compositions computed in the OECD/BSAF benchmark. Samples were heated in an induction furnace to simulate thermal cutting and released aerosols were collected during three temperature ramps using impactors. The collected aerosols were chemically analyzed by ICP-AES and ICP-MS. Iron and tin are the major elements found in these aerosols, followed by chromium and silicon. Significant releases of tellurium, barium and cerium were observed.
長谷川 邦夫; Strnadel, B.*; Li, Y.; Lacroix, V.*
Journal of Pressure Vessel Technology, 144(6), p.061202_1 - 061202_6, 2022/12
被引用回数:2 パーセンタイル:17.22(Engineering, Mechanical)配管の肉厚が薄いとき、未貫通亀裂は貫通亀裂になりやすく、冷却材の漏洩の可能性が高まる。ASME Code Section XIでは、薄肉配管に対して貫通亀裂の最終許容角度が定められている。この最終許容角度は、もし未貫通亀裂が貫通亀裂になったとき、塑性崩壊しないように設けられている。この安定性を保つために貫通亀裂の塑性崩壊応力が許容応力と組み合わされている。しかしながら、薄肉配管の貫通亀裂の最終許容角度が求められない。この論文は貫通亀裂の塑性崩壊応力と未貫通亀裂の許容応力を比較する。これらの応力の比較により、貫通亀裂の最終許容応力式を導いた。この角度を、厳密解として表すとともに、オプションとして種々な運転状態における近似解で表すことができた。
長谷川 邦夫; Strnadel, B.*; Lacroix, V.*; Udyawar, A.*
International Journal of Pressure Vessels and Piping, 199, p.104722_1 - 104722_5, 2022/10
被引用回数:1 パーセンタイル:14.82(Engineering, Multidisciplinary)周方向亀裂を有する高靭性配管が引張り荷重を受けるときの塑性崩壊応力は極限荷重クライテリアで予測される。この極限荷重クライテリアはASME Code Section XIで与えられており、未貫通亀裂の許容膜応力は、塑性崩壊応力と安全率の組み合わせで決定される。ここで、許容応力は亀裂角度が大になると減小する。亀裂角度が大になると、未貫通亀裂である許容応力は貫通亀裂より大になる。このような許容応力は不安定になり、特に薄肉配管にとっては健全性を損なう恐れがある。このような懸念を払拭するために最大亀裂角度を設定する必要がある。本報告は、貫通亀裂の塑性崩壊応力を基にして、許容応力に最大許容亀裂角度の設定を提案するものである。
Lacroix, V.*; 長谷川 邦夫; Li, Y.; 山口 義仁
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 7 Pages, 2022/07
The structural integrity assessment of pipes with circumferential surface flaw under the plastic collapse regime consists of net section collapse analysis. In recent years various researchers showed that this analysis, which has been developed based on classic beam theory, suffers from certain inaccuracies. As such, assessment purely based on net-section collapse and beam theory can reveal both conservative and unconservative results. To address those inaccuracies, in this paper authors introduced a correction factor which aims to mitigate the difference between the ASME B&PV Code Section XI equations and the experimental results. This correction factor is calculated using an empirical formula developed on the basis of a large experimental database of pipe collapse bending tests containing variety of diameter, thickness, flaw depth and flaw length values. Within this work, authors took a systematic approach to identify the most influencing factors on such a correction factor and showed that by applying this correction factor to the current solution of ASME B&PV Code Section XI, this solution becomes more accurate. This corrected approach also is in line with ASME B&PV Code Section XI Appendix C practice for axial flaw in pipes, where a semi-empirical correction factor has been considered as well.
山口 義仁; 長谷川 邦夫; Li, Y.; Lacroix, V.*
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 4 Pages, 2022/07
Four-point bending tests without internal pressure were performed for Type 304 stainless steel pipes with circumferential flaws at room temperature. The specimens are 1-inch diameter (33.7 mm) Schedule 160 pipes (6.3 mm wall thickness). The flaws were part-through flaws located at the pipe external side. The flaw angles are from 120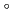 to 240
to 240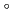 , and the flaw depths are two cases of 50% and 75% of the wall thickness. Plastic collapse stresses obtained from experiments were compared with those calculated using Limit Load Criteria from Appendix C of the American Society of Mechanical Engineers Code Section XI. Limit Load Criteria were developed using flow stress at flawed section of the pipe. The plastic collapse stress test results were larger than those of the calculation results. For flaws with flaw depths less than 50% of the wall thickness, the experimental stresses were significantly large. The Limit Load Criteria given by Section XI provide conservative collapse stresses and could be improved.
, and the flaw depths are two cases of 50% and 75% of the wall thickness. Plastic collapse stresses obtained from experiments were compared with those calculated using Limit Load Criteria from Appendix C of the American Society of Mechanical Engineers Code Section XI. Limit Load Criteria were developed using flow stress at flawed section of the pipe. The plastic collapse stress test results were larger than those of the calculation results. For flaws with flaw depths less than 50% of the wall thickness, the experimental stresses were significantly large. The Limit Load Criteria given by Section XI provide conservative collapse stresses and could be improved.
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫; Mares, V.*
Proceedings of ASME 2022 Pressure Vessels and Piping Conference (PVP 2022) (Internet), 7 Pages, 2022/07
現行のASME Code Section XIでは、非平面状欠陥に対して簡易的な手法が提案されている。すなわち、非平面状欠陥面を最大主応力方向に投影し2つの平面状欠陥に分解する。しかしながら、この非平面状欠陥の簡易的な投影は荷重に対して、あるいは非平面状欠陥の傾きに対して常に保守的であると言えない場合がある。本論文は、ASME Codeのアプローチに保守性のある包括的な評価を実施し、現行のASME Code Section XIの不適正を克服した非平面状欠陥の代替アプローチを提案する。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫
Proceedings of ASME 2021 Pressure Vessels and Piping Conference (PVP 2021) (Internet), 5 Pages, 2021/07
欠陥が検出されたとき、この欠陥を有する耐圧機器の健全性はASME Section XI等の規格によって評価される。評価の最初のステップでは、検出された欠陥の形状を定める欠陥のモデル化を行うことである。ASME Section XIにおける欠陥モデル化手法では、非平面状欠陥は最大主応力方向に投影して、2つの平面状欠陥に分離して扱うように規定されている。このアプローチは欠陥評価を簡素化しているが、保守性が含まれている。本論文では、この欠陥モデル化手法の改善提案を行うために、現状の欠陥モデル化手法に基づく投影された平面状欠陥の応力拡大係数と実際の非平面状欠陥の混合モードの応力拡大係数について比較検討を行った。
Desclaux, C.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of ASME 2021 Pressure Vessels and Piping Conference (PVP 2021) (Internet), 10 Pages, 2021/07
亀裂を有する管の塑性崩壊曲げモーメントを推定する式は力学的平衡に基づくASME Section XIの簡便式で与えられている。著者の一人が、この簡便式は亀裂が管の外表面にあるときは非安全側の評価になると指摘し、亀裂リガメントの平均半径を考慮した式を提案した。本報では、さらに亀裂を有する断面の中立軸の位置を正確に考慮した塑性崩壊曲げモーメントの式を導いた。その結果、亀裂が管の外表面にあるとき、提案式による塑性崩壊曲げモーメントと比べるとASME Section XIの既存式は非保守的であることが分かった。
Dulieu, P.*; Lacroix, V.*; 長谷川 邦夫
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 7 Pages, 2020/08
検出された欠陥が近接している場合、維持規格で与えられる合体ルールにより、互いに干渉しあう欠陥は1つの欠陥に合体される。ASME Code Case N877-1は、複数の半径方向の平面状欠陥に対して代替合体ルールとして用意されたものである。欠陥の干渉の計算は、膜応力の下で実施されてきた。しかしながら、実際の機器に作用する付加荷重は一様な応力ではない。この論文の目的は、付加応力分布に曲げ応力が存在する場合のASME Code Case N877-1の妥当性を評価することにある。この目的のため、種々な応力分布と欠陥形状をカバーするようにした。欠陥の干渉に及ぼす効果は3次元のXEEM解析で評価した。
Lacroix, V.*; Dulieu, P.*; 長谷川 邦夫; Mare , V.*
, V.*
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 8 Pages, 2020/08
耐圧機器に複数欠陥が検出されたとき、欠陥の形状をはっきりと決めるために欠陥の特性化(形状の作成化)が行われる。この特性化は維持規格のルールに従ってなされる。最初のステップは、欠陥と機器の自由表面の干渉であり、2番目に欠陥と欠陥の干渉である。ASME Code Sec. XIでは如何にして欠陥の合体と自由表面の干渉の扱いが欠けており、欠陥の特性化が明確になっていない。いくつかの非現実な欠陥の配列ではあるが欠陥評価の代表例を図で論文の中に示す。この論文は、IWA-3300, IWB/IWC-3510-1の欠陥の特性化における合体欠陥の扱いを明確にするためにASME Codeの改定の技術根拠として用いられる。
長谷川 邦夫; Li, Y.; Lacroix, V.*; Mare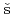 , V.*
, V.*
Proceedings of ASME 2020 Pressure Vessels and Piping Conference (PVP 2020) (Internet), 6 Pages, 2020/08
正味応力概念を基に新たに精度の高いModified Limit Load Criteriaを用いて、周方向に欠陥を有する高靭性配管の破壊応力を求める式を開発した。一方、ASME Code Section XIで規定されているLimit Load Criteriaでも破壊応力が求められる。両式による破壊応力の比較の結果、ASME Codeによる外表面欠陥に対してASME Codeでは常に大きく、ASME Codeは非安全側であることを見出している。ASME Codeには評価不要欠陥基準が規定されており、これをModified Limit Load Criteriaで検討した。評価不要欠陥基準は許容される欠陥深さが小さいことから、両手法による差は極めて小さく、現行のASME Code Section XIの評価不要欠陥基準を外表面欠陥に適用しても問題ないことを見出した。
長谷川 邦夫; Li, Y.; Lacroix, V.*; Mare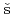 , V.*
, V.*
Journal of Pressure Vessel Technology, 142(3), p.031506_1 - 031506_7, 2020/06
被引用回数:1 パーセンタイル:5.70(Engineering, Mechanical)周方向に亀裂を有する管の曲げによる塑性崩壊応力はASME Section XI規格のAppendix Cで用意されている極限荷重評価法で推定される。この推定式は管の内外表面の亀裂に適用される。しかし、近年著者らが開発した精度の高い式によると、管の外表面にある亀裂の管は、塑性崩壊応力は小さく、Appendix Cの式を用いると非安全側になることを報告してきた。本報はこの精度の高い式を用いてAppendix Cの式の適用限界を明らかにした。